Классический метод расчета переходных процессов основан на составлении и последующем решении (интегрировании) дифференциальных уравнений, составленных по законам Кирхгофа и связывающих искомые токи и напряжения послекоммутационной цепи и заданные воздействующие функции (источники электрической энергии).
Порядок ДУ определяется числом независимых начальных условий. Другой способ – по формуле: 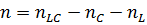 , где
, где 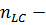 число реактивных элементов,
число реактивных элементов, 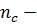 число независимых емкостных контуров,
число независимых емкостных контуров, 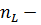 число независимых индуктивных узлов.
число независимых индуктивных узлов.
Независимый емкостной контур – контур, образованный только ёмкостями или ёмкостями и независимыми источниками напряжения.
Независимый индуктивный узел – узел, к которому подключены только индуктивности или индуктивности и независимые источники тока.
При этом падение напряжений в активных сопротивлениях r и на реактивных элементах: конденсаторе C и катушке индуктивности L определяются соответственно: 
Преобразуя систему уравнений, можно вывести итоговое дифференциальное уравнение относительно какой-либо одной переменной величины x (t): 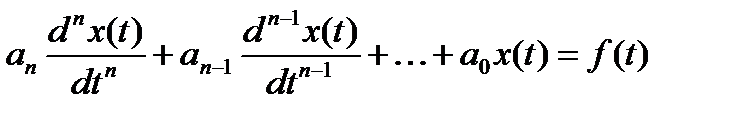 .
.
Здесь n – порядок дифференциального уравнения, он же – порядок цепи, коэффициенты ak > 0 и определяются параметрами пассивных элементов R, L, C цепи, а правая часть является функцией задающих воздействий.
В соответствии с классической теорией ДУ полное решение НДУ находится в виде суммы частного решения НДУ и общего решения однородного дифференциального уравнения:
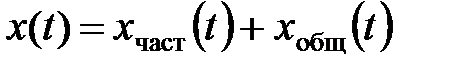 .
.
Частное решение полностью определяется видом правой части f (t) дифференциального уравнения. Зависит от воздействующих источников электрической энергии, поэтому вид 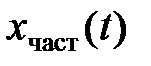 обуславливается источниками электрической энергии и называется принужденной составляющей
обуславливается источниками электрической энергии и называется принужденной составляющей 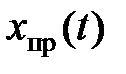 .
.
Общее решение 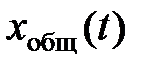 однородного дифференциального уравнения зависит от корней характеристического уравнения, которые определяются коэффициентами дифференциального уравнения, и не зависит от правой части.
однородного дифференциального уравнения зависит от корней характеристического уравнения, которые определяются коэффициентами дифференциального уравнения, и не зависит от правой части. 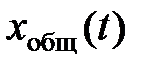 не зависит от воздействующих источников и по этой причине называется свободной составляющей
не зависит от воздействующих источников и по этой причине называется свободной составляющей  и полностью определяется параметрами пассивных элементов цепи, а физически процессом перераспределения запасов энергии электрического и магнитного полей в реактивных элементах цепи.
и полностью определяется параметрами пассивных элементов цепи, а физически процессом перераспределения запасов энергии электрического и магнитного полей в реактивных элементах цепи.
Таким образом, любая искомая величина в переходном режиме
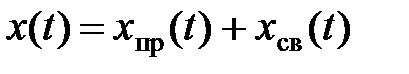 .
.
Свободную составляющую  переходного процесса ищут в виде
переходного процесса ищут в виде
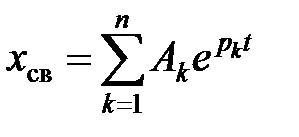 ,
,
где n – порядок цепи, совпадающий с порядком дифференциального уравнения;
pk – корни характеристического уравнения (собственные числа цепи);
Ak – постоянные интегрирования.
Следует заметить, что свободный процесс происходит в цепи, освобожденной от источников энергии. При отсутствии источников свободные токи и напряжения должны со временем затухать. Следовательно, вещественные корни характеристических уравнений или вещественные части комплексно-сопряженных корней должны быть отрицательными.
Вид свободной составляющей переходного процесса определяется числом и значениями корней характеристического уравнения:
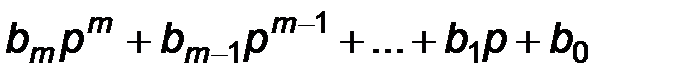 = 0.
= 0.
В случае, когда корни 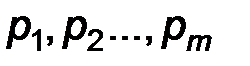 характеристического уравнения вещественные и различные, решение имеет вид:
характеристического уравнения вещественные и различные, решение имеет вид:
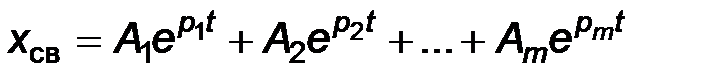 ,
,
где А1, А2, …, Аm – постоянные интегрирования, которые находятся из начальных условий задачи.
В случае, когда корни уравнения – вещественные и равные, т. е.
p1 = p2 = …pm = p, свободная составляющая определяется уравнением:
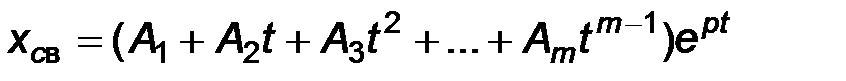 .
.
Если корни комплексно-сопряженные 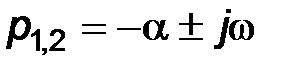 , тогда решение имеет вид:
, тогда решение имеет вид: 
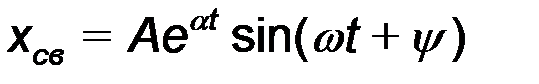 , где А и
, где А и 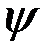 – постоянные интегрирования, определяемые также из начальных условий задачи.
– постоянные интегрирования, определяемые также из начальных условий задачи.
Если число корней характеристического уравнения больше одного, то необходимо иметь не только начальные условия искомой переменной, но и ее производных. При этом порядок производных, начальное значение которых необходимо знать, на единицу меньше числа корней характеристического уравнения. Для определения производных при  уравнения Кирхгофа дифференцируют и решают совместно для
уравнения Кирхгофа дифференцируют и решают совместно для  .
.
Данный метод применяют для решения дифференциальных уравнений первого и второго порядка. При более высоких порядках определение постоянных интегрирования и решение характеристического уравнения представляет собой сложный процесс.
Последовательность:
· Вычислить начальные независимые условия. 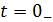
а) Постоянные источники: 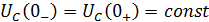
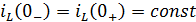 б) Синусоидальные источники:
б) Синусоидальные источники: 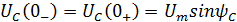
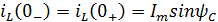
· Вычислить зависимые условия. 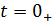
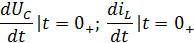
· Вычислить вынужденную составляющую. 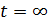
а) 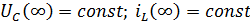
б) 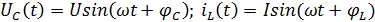
· Составляется характеристическое уравнение и считаются его корни. Корни определяют вид свободной составляющей.
· Записываем ответ в виде:
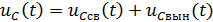
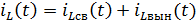 , уже найдя все постоянные интегрирования.
, уже найдя все постоянные интегрирования.
Основные этапы решения классическим методом:
1. Определение начальных условий
2. Определение дифференциального уравнения
3. Определение характеристического уравнения
4. Определение свободной составляющей
5. Определение принуждённой составляющей
6. Определение неизвестных констант
7. Проверка полученного решения



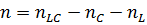 , где
, где 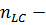 число реактивных элементов,
число реактивных элементов, 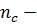 число независимых емкостных контуров,
число независимых емкостных контуров, 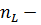 число независимых индуктивных узлов.
число независимых индуктивных узлов.
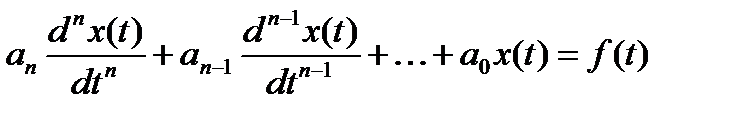 .
.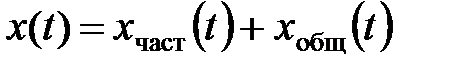 .
.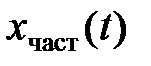 обуславливается источниками электрической энергии и называется принужденной составляющей
обуславливается источниками электрической энергии и называется принужденной составляющей 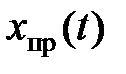 .
.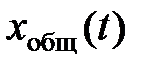 однородного дифференциального уравнения зависит от корней характеристического уравнения, которые определяются коэффициентами дифференциального уравнения, и не зависит от правой части.
однородного дифференциального уравнения зависит от корней характеристического уравнения, которые определяются коэффициентами дифференциального уравнения, и не зависит от правой части.  и полностью определяется параметрами пассивных элементов цепи, а физически процессом перераспределения запасов энергии электрического и магнитного полей в реактивных элементах цепи.
и полностью определяется параметрами пассивных элементов цепи, а физически процессом перераспределения запасов энергии электрического и магнитного полей в реактивных элементах цепи.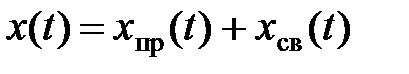 .
.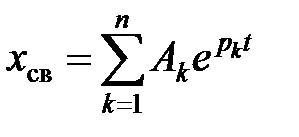 ,
,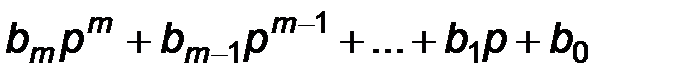 = 0.
= 0.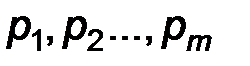 характеристического уравнения вещественные и различные, решение имеет вид:
характеристического уравнения вещественные и различные, решение имеет вид: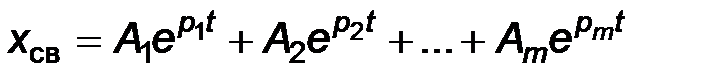 ,
,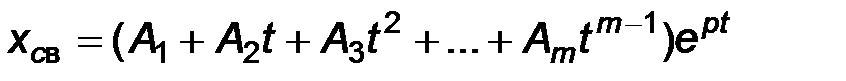 .
.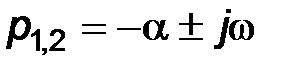 , тогда решение имеет вид:
, тогда решение имеет вид: 
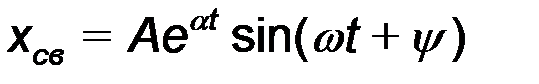 , где А и
, где А и 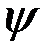 – постоянные интегрирования, определяемые также из начальных условий задачи.
– постоянные интегрирования, определяемые также из начальных условий задачи. уравнения Кирхгофа дифференцируют и решают совместно для
уравнения Кирхгофа дифференцируют и решают совместно для 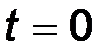 .
.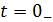
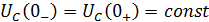
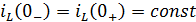 б) Синусоидальные источники:
б) Синусоидальные источники: 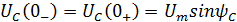
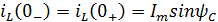
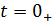
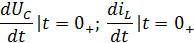
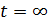
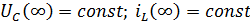
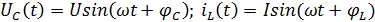
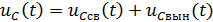
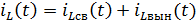 , уже найдя все постоянные интегрирования.
, уже найдя все постоянные интегрирования.


