
· 42. Ортогональная проекция - это частный случай параллельного проецирования. При ортогональном проецировании проецирующие лучи перпендикулярны к плоскости проекций.
· Аппарат такого проецирования состоит из одной плоскости проекций.
· Чтобы получить ортогональную проекцию точки А, через неё надо провести проецирующий луч перпендикулярно к П1. Точка А1 называется ортогональной или прямоугольной проекцией точки А.
·  Чтобы получить ортогональную проекцию А1В1 отрезка АВ, на плоскость П1, необходимо через точки А и В провести проецирующие прямые, перпендикулярные П1. При пересечении проецирующих прямых с плоскостью П1 получатся ортогональные проекции А1 и В1 точек А и В. Соединив ортогональные проекции А1 и В1 получим ортогональную проекцию А1В1 отрезка АВ.
Чтобы получить ортогональную проекцию А1В1 отрезка АВ, на плоскость П1, необходимо через точки А и В провести проецирующие прямые, перпендикулярные П1. При пересечении проецирующих прямых с плоскостью П1 получатся ортогональные проекции А1 и В1 точек А и В. Соединив ортогональные проекции А1 и В1 получим ортогональную проекцию А1В1 отрезка АВ.
· Все свойства параллельного проецирования выполнимы и для ортогонального проецирования. Однако ортогональные проекции обладают ещё некоторыми свойствами.
· Свойство ортогонального проецирования:
· Для ортогонального проецирования будет справедлива теорема о проецировании прямого угла:
· Теорема: Если хотя бы одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то угол на эту плоскость проецируется в натуральную величину.
·
43 Площадь ортогональной проекции плоской фигуры на плоскость
· Теорема. Площадь ортогональной проекции плоской фигуры на плоскость есть произведение площади самой фигуры на косинус угла между плоскостью фигуры и плоскостью проекции.
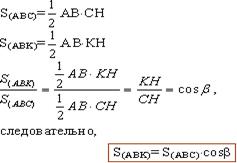
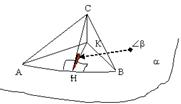 Доказательство. Докажем теорему на примере треугольника. Пусть дана плоскость a и треугольник АВС. Рассмотрим общий случай, когда плоскость a и плоскость треугольника лежат под некоторым острым углом друг к другу. Для упрощения решения плоскость a проведем через одну из сторон треугольника, например сторону АВ. Значит после проектирования точки А и В передут в себя, а точка С переедет в точку К. В треугольнике АВС проведем высоту СН из вершины С. В треугольнике АВК соединим точки К и Н. Прямая КН перпендикулярна прямой АВ (КН – проекция прямой СН на плоскость a, СН ^ АВ,? КН ^ АВ по теореме о трех перпендикулярах). Таким образом, угол СНК – двугранный угол между плоскостями, обозначим его за b. Выразим площадь треугольников АВС и АВК и найдем их отношение:
Доказательство. Докажем теорему на примере треугольника. Пусть дана плоскость a и треугольник АВС. Рассмотрим общий случай, когда плоскость a и плоскость треугольника лежат под некоторым острым углом друг к другу. Для упрощения решения плоскость a проведем через одну из сторон треугольника, например сторону АВ. Значит после проектирования точки А и В передут в себя, а точка С переедет в точку К. В треугольнике АВС проведем высоту СН из вершины С. В треугольнике АВК соединим точки К и Н. Прямая КН перпендикулярна прямой АВ (КН – проекция прямой СН на плоскость a, СН ^ АВ,? КН ^ АВ по теореме о трех перпендикулярах). Таким образом, угол СНК – двугранный угол между плоскостями, обозначим его за b. Выразим площадь треугольников АВС и АВК и найдем их отношение:
44. Векторы в пространстве - основные определения.
Вектор – это направленный отрезок прямой.
То есть, в качестве вектора мы принимаем отрезок на плоскости или в пространстве, считая одну из его граничных точек началом, другую – концом.
Для обозначения векторов будем использовать строчные латинские буквы со стрелочкой над ними, например  . Если заданы граничные точки начала и конца отрезка, к примеру А и В, то вектор будем обозначать как
. Если заданы граничные точки начала и конца отрезка, к примеру А и В, то вектор будем обозначать как  .
.
Определение. Нулевой вектор  – это любая точка плоскости или пространства.
– это любая точка плоскости или пространства.
Будем считать, что нулевому вектору можно придать любое направление на плоскости и в пространстве.

Определение. Длина вектора  - это неотрицательное число, равное длине отрезка АВ.
- это неотрицательное число, равное длине отрезка АВ.
Длину вектора  будем обозначать как
будем обозначать как  .
.
Так как обозначение длины вектора в точности совпадает со знаком модуля, то можно услышать, что длину вектора называют модулем вектора. Все же рекомендуем использовать термин "длина вектора". Длина нулевого вектора равна нулю.
Коллинеарные векторы
Коллинеарные векторы это векторы, лежащие на параллельных прямых (или на одной и той же прямой).
Векторы а, b, c коллинеарны. Векторы АС, BD, и СВ коллинеарны.
Коллинеарные векторы могут иметь одно и то же направление (равнонаправленные векторы) или противоположные.
Так, векторы а и с равнонаправлены, векторы а и b (а также b и c) противоположно направлены. Векторы АС и BD равнонаправлены, векторы АС и СВ противоположно направлены.
47. Компланарные векторы
Векторы, которые параллельны одной плоскости или лежат на одной плоскости, называются компланарными векторами.
Три вектора называются компланарными, если они, будучи приведёнными к общему началу, лежат в одной плоскости.
Всегда возможно найти плоскость, параллельную двум произвольным векторам, поэтому любые два вектора всегда компланарные.
Eсли из трёх векторов два коллинеарны, то очевидно, что эти три вектора компланарны.




 Чтобы получить ортогональную проекцию А1В1 отрезка АВ, на плоскость П1, необходимо через точки А и В провести проецирующие прямые, перпендикулярные П1. При пересечении проецирующих прямых с плоскостью П1 получатся ортогональные проекции А1 и В1 точек А и В. Соединив ортогональные проекции А1 и В1 получим ортогональную проекцию А1В1 отрезка АВ.
Чтобы получить ортогональную проекцию А1В1 отрезка АВ, на плоскость П1, необходимо через точки А и В провести проецирующие прямые, перпендикулярные П1. При пересечении проецирующих прямых с плоскостью П1 получатся ортогональные проекции А1 и В1 точек А и В. Соединив ортогональные проекции А1 и В1 получим ортогональную проекцию А1В1 отрезка АВ. Доказательство. Докажем теорему на примере треугольника. Пусть дана плоскость a и треугольник АВС. Рассмотрим общий случай, когда плоскость a и плоскость треугольника лежат под некоторым острым углом друг к другу. Для упрощения решения плоскость a проведем через одну из сторон треугольника, например сторону АВ. Значит после проектирования точки А и В передут в себя, а точка С переедет в точку К. В треугольнике АВС проведем высоту СН из вершины С. В треугольнике АВК соединим точки К и Н. Прямая КН перпендикулярна прямой АВ (КН – проекция прямой СН на плоскость a, СН ^ АВ,? КН ^ АВ по теореме о трех перпендикулярах). Таким образом, угол СНК – двугранный угол между плоскостями, обозначим его за b. Выразим площадь треугольников АВС и АВК и найдем их отношение:
Доказательство. Докажем теорему на примере треугольника. Пусть дана плоскость a и треугольник АВС. Рассмотрим общий случай, когда плоскость a и плоскость треугольника лежат под некоторым острым углом друг к другу. Для упрощения решения плоскость a проведем через одну из сторон треугольника, например сторону АВ. Значит после проектирования точки А и В передут в себя, а точка С переедет в точку К. В треугольнике АВС проведем высоту СН из вершины С. В треугольнике АВК соединим точки К и Н. Прямая КН перпендикулярна прямой АВ (КН – проекция прямой СН на плоскость a, СН ^ АВ,? КН ^ АВ по теореме о трех перпендикулярах). Таким образом, угол СНК – двугранный угол между плоскостями, обозначим его за b. Выразим площадь треугольников АВС и АВК и найдем их отношение:
 . Если заданы граничные точки начала и конца отрезка, к примеру А и В, то вектор будем обозначать как
. Если заданы граничные точки начала и конца отрезка, к примеру А и В, то вектор будем обозначать как  .
. – это любая точка плоскости или пространства.
– это любая точка плоскости или пространства.
 .
.




