Сначала изложим метод наименьших квадратов в невероятностной интерпретации, как метод решения задачи аппроксимации.
Начнём с простейшего – линейного – случая. На плоскости дано множество точек (xi, yi), i =1, 2, ¼, n, явно располагающихся вблизи некоторой прямой. Из-за того, что глазу из всех линий проще всего выделить прямую, и того, что линейный случай часто встречается на практике, этот случай и занял особое место. Требуется в каком-то смысле наилучшим образом провести прямую, вокруг которой группируются точки. Обычно выбирают прямую, руководствуясь принципом наименьших квадратов: ищут прямую y =q1 x +q0, максимизирующую сумму квадратов
d=  (yi -q1 xi -q0)2.
(yi -q1 xi -q0)2.
Разность yi -q1 xi -q0интерпретируется как ошибка отклонения ординаты
i -ой точки от искомой прямой. Выбор в качестве меры отклонения точек (xi, yi) от точек прямой – суммы квадратов ошибок условен: можно было бы взять, например, сумму модулей или сумму четвёртых степеней, однако это вызвало бы дополнительные аналитические и вычислительные трудности без видимых преимуществ. Как и все принципы, принцип наименьших квадратов не требует доказательства; он опирается на здравый смысл, а его полезность и разумность подтверждается практическим его применением.
Найдем прямую, минимизирующую d, обычным способом:
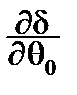 =-2
=-2  (yi -q1 xi -q0)=0,
(yi -q1 xi -q0)=0,
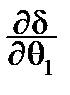
=-2

(
yi -q
1 xi -q
0)
xi =0,
или
q
1  xi
xi +q
0 n =
 yi
yi,
q
1  xi 2
xi 2+q
0  xi
xi =
 yixi
yixi.
Решение очевидно:
q
1=
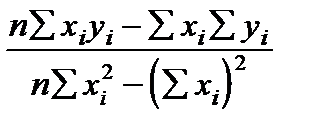
,
q
0=

.
Аналогично по множеству точек (xi, yi) можно искать аппроксимирующий полином y =q0+q1 x +q2 x 2+¼+q kxk степени k. При этом мы должны минимизировать сумму квадратов
d=  (yi -q0-q1 xi -q2 xi 2-¼-q kxik)2.
(yi -q0-q1 xi -q2 xi 2-¼-q kxik)2.
Соответствующая система уравнений для неизвестных коэффициентов q0, q1, ¼, q k называется системой нормальных уравнений и имеет вид:
q
0 n +q
1S
xi +¼+q
k S
xik =S
yi,
q
0S
xi +q
1S
xi 2+¼+q
k S
xik +1=S
xiyi,
...........................
q
0S
xik +q
1S
xik +1+¼+q
k S
xi 2 k =S
xikyi,
В каждой сумме индекс суммирования i меняется от 1 до n.
Решение полученной системы линейных неоднородных уравнений легко определяется по правилу Крамера.
Удобно записать систему нормальных уравнений в сокращённом матричном виде. Для этого определим три матрицы-столбца:
X = 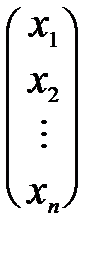 , Y =
, Y = 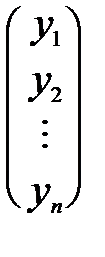 , Q=
, Q=  ,
,
и так называемую структурную матрицу размера (k +1)´ n:
A = 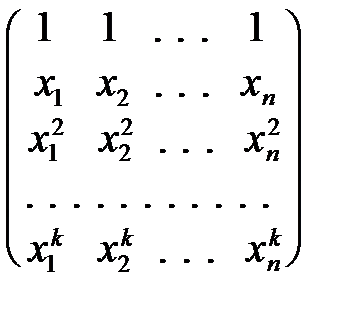 .
.
Тогда легко проверить, что система нормальных уравнений записывается в форме:
AAT Q= AY,
где AT – матрица, транспонированная по отношению к матрице A.
Если матрица AAT имеет обратную, то решение системы нормальных уравнений сразу выписывается
Q=(AAT)-1 AY.
Формулы линейного случая входят сюда как частный случай при k =1.
Заменой функций и переменных к рассмотренным случаям можно свести и многие неполиномиальные зависимости. Например, для y =q1ln x +q0, вместо точек (xi, yi) можно рассматривать точки (ln xi, yi): получаем линейную зависимость с помощью введения логарифмического масштаба по одной из осей.
Для функции y = 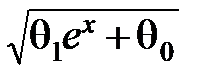 следует взять точки (exi, yi 2), i =1, 2, ¼, n, и т. д.
следует взять точки (exi, yi 2), i =1, 2, ¼, n, и т. д.
Полиномиальная аппроксимация часто появляется в следующем варианте: если мы аппроксимируем точки функцией f (x), то для аналитических функций бывает возможно ограничиться частью степенного ряда, дающей достаточную точность.
Описанная задача часто применяется практиками, и в таком виде метод наименьших квадратов не имеет никакого отношения к теории вероятностей. Он возникает как задача аппроксимации, как сокращённый аналитический способ представления наблюдений.
Вероятностный аспект появляется, например, в такой ситуации: имеются две физические величины, связанные детерминированным законом
y =q0+q1 x +q2 x 2+¼+q kxk,
но значения коэффициентов неизвестны и строгое выполнение закона не вызывает сомнений. Значение переменной x при эксперименте пусть задаётся точно, а в измерение величины y вкрадываются ошибки, так что опытные точки (xi, yi), i =1, 2, ¼, n, могут даже не удовлетворять уравнению. Если бы ошибок при измерении величины y не было, то достаточно было бы (k +1) наблюдений, чтобы найти все коэффициенты. Ошибки приводят к тому, что, если пытаться решать систему
yi =q0+q1 xi +q2 xi 2+¼+q kxik, i =1, 2, ¼, n,
то она обычно оказывается противоречивой, несовместной.
Выход указывает принцип наименьших квадратов. Состоит он в том, чтобы выбрать коэффициенты, минимизируя сумму квадратов ошибок
d=  e i 2, e i = yi -(q0+q1 xi +q2 xi 2+¼+q kxik).
e i 2, e i = yi -(q0+q1 xi +q2 xi 2+¼+q kxik).
Вероятностный подход даёт возможность увидеть, когда принцип наименьших квадратов, как он сформулирован, хорош и когда плох. В сумму d те точки, которые лежат на искомой кривой, вносят нулевой вклад; наибольший же вклад вносят наиболее ошибочные наблюдения, именно они и начинают особенно заметно влиять на результат, хотя менее всего заслуживают такого влияния. В особенности плохо, когда на оси Ox есть участки наиболее точных измерений и участки очень грубых измерений. Участки грубых наблюдений получают право определять сумму, вносить в неё основной вклад. Ясно, что наиболее естественный случай применения принципа наименьших квадратов – случай, когда априори средний квадрат ошибок одинаков во всех наблюдениях. Если систематических погрешностей в измерениях нет, т. е. M e i =0 для " i, то это означает, что дисперсии ошибок должны быть одинаковы, или как говорят, наблюдения должны быть равноточными.
Если же наблюдения не равноточные, но дисперсии известны: D e i =s i 2, то можно внести коррективы в принцип наименьших квадратов, введя в сумму d весовые множители, уравнивающие априорный вклад в сумму всех наблюдений, минимизировать
d= 
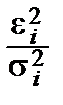 .
.
К сожалению, как правило, параметры s i 2бывают неизвестны, и практики обрабатывают наблюдения так, словно они равноточные.
Чаще всего, когда путем замены x и y приводят зависимость y = f (x) к линейной или полиномиальной с целью применить метод наименьших квадратов, то нарушают именно равноточностъ измерений, если она до этого была, придавая повышенный вес одним участкам наблюдений перед другими, причём обычно этот факт практиками молчаливо игнорируется. По поводу этого, однако, можно сказать, как и по поводу любого принципа, что если последствия его применения, связанные с ним ошибки нас устраивают, не чрезмерны, то всё в порядке.
В таком изложении метод наименьших квадратов применим к ошибкам e i, как угодно распределённым. Если же ошибки распределены по нормальному закону: e i ~ N (0, s i), то полученные по методу наименьших квадратов оценки параметров q0, q1, ¼, q k совпадают с их оценками по методу максимального правдоподобия: ведь неизвестные коэффициенты q0, q1, ¼, q k становятся параметрами распределения случайной величины y.



 (yi -q1 xi -q0)2.
(yi -q1 xi -q0)2.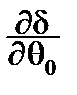 =-2
=-2 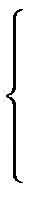
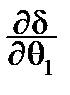 =-2
=-2 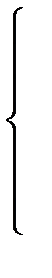
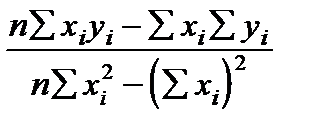 ,
, .
.
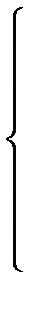
 , Y =
, Y = 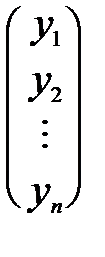 , Q=
, Q=  ,
, .
.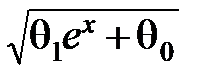 следует взять точки (exi, yi 2), i =1, 2, ¼, n, и т. д.
следует взять точки (exi, yi 2), i =1, 2, ¼, n, и т. д.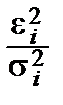 .
.


