Пусть X ~ F (x, q), причём вид функции распределения F (x, q) известен, а параметр q неизвестен (считаем его одномерным). Требуется по выборке указать такой интервал [  ,
, 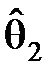 ], который с заданной вероятностью a накрывает неизвестный параметр q:
], который с заданной вероятностью a накрывает неизвестный параметр q:
P {  £q£
£q£ 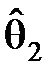 }=a.
}=a.
Сам интервал [  ,
, 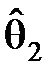 ] называется доверительным, а a – доверительной вероятностью. Концы интервала – функции от выборки:
] называется доверительным, а a – доверительной вероятностью. Концы интервала – функции от выборки:
 =
=  (x 1, x 2, ¼, xn),
(x 1, x 2, ¼, xn), 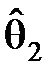 =
= 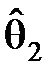 (x 1, x 2, ¼, xn)
(x 1, x 2, ¼, xn)
и являются случайными величинами. Желательно иметь a близким к единице, а интервал – поменьше. Однако увеличивая a, мы будем получать всё более широкие интервалы и тем самым всё менее информативные интервалы, всё менее интересные. Желательным свойством можно считать условие:  -
- 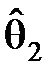
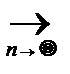 0, тогда при достаточно большом числе наблюдений можно как угодно точно локализовать параметр q.
0, тогда при достаточно большом числе наблюдений можно как угодно точно локализовать параметр q.
В качестве a обычно берут числа 0,99, 0,95, 0,9. Выбор доверительной вероятности зависит от практических последствий в случае, когда доверительный интервал не накроет q. При a=0,9 следует ожидать, что в среднем мы будем промахиваться в десятой части всех применений данного доверительного интервала. Если это не страшно, то можно брать a=0,9. Если же нас в этих случаях ждут большие материальные потери или это ведёт к опасностям для человеческой жизни, то такая доверительная вероятность недопустимо мала.
Легко строить доверительный интервал для q, если мы имеем для параметра точечную оценку  (x 1, x 2, ¼, xn) и хотя бы приближённо знаем закон её распределения. Именно в этом случае по закону распределения
(x 1, x 2, ¼, xn) и хотя бы приближённо знаем закон её распределения. Именно в этом случае по закону распределения  , задавая a, мы можем находить такое e, чтобы
, задавая a, мы можем находить такое e, чтобы
P {|  -q|£e}=a.
-q|£e}=a.
Иногда a называют надёжностью оценки, а e – её точностью. Здесь можно переписать неравенство под знаком вероятности в следующем виде:
P {  -e£q£
-e£q£  +e}=a,
+e}=a,
и искомый доверительный интервал имеет вид [  -e,
-e,  +e] и длину 2e.
+e] и длину 2e.
Разберём несколько задач на построение доверительных интервалов.
1°. Приближённый доверительный интервал для вероятности события.
Пусть имеется событие A и для его вероятности P (A)= p мы хотим построить доверительный интервал, сделав n опытов. Допустим, что в этих опытах событие A наступило m раз.
По интегральной теореме Муавра-Лапласа:
P { a £  £ b }»
£ b }» 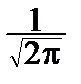
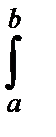
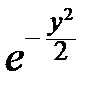 dy.
dy.
Возьмём a =-e, b =e:
P {|  |£e}»
|£e}» 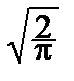
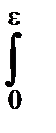
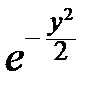 dy =F(e), "e>0.
dy =F(e), "e>0.
Стоящее под знаком вероятности неравенство заменим равносильным:
P { m 2-2 mnp + n 2 p 2£e2 npq }»F(e), "e>0,
или, заменяя q на 1- p:
P { p 2(n 2+e2 n)- p (2 mn +e2 n)+ m 2£0}»F(e), "e>0.
Кривая y = p 2(n 2+e2 n)- p (2 mn +e2 n)+ m 2 как функция p является параболой.
Пусть её корни p 1, p 2, причём p 1< p 2, т. е.
P { p 1£ p £ p 2}»F(e), "e>0
и теперь мы можем указать процедуру построения доверительного интервала для p:
a) Задаём доверительную вероятность a.
b) По a находим e из уравнения F(e)=a; корень уравнения легко определяется с помощью таблицы функции Лапласа.
c) Решаем квадратное уравнение p 2(n 2+e2 n)- p (2 mn +e2 n)+ m 2=0, находим его корни p 1, p 2, p 1< p 2.
d) Искомый приближённый доверительный интервал имеет вид: [ p 1, p 2].
Точность этого интервала зависит от того, достаточно ли мала ошибка при использовании теоремы Муавра-Лапласа, можно ли практически считать, что
m ~ N (np, 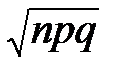 ).
).
2°. Доверительный интервал для параметра a нормального закона при известном s.
Пусть X ~ N (a, s), причём s известно.
Получаем выборку (x 1, x 2, ¼, xn). Среднее выборочное:  ~ N (a,
~ N (a, 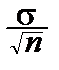 ). Его нормированное уклонение:
). Его нормированное уклонение:
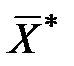 =
= 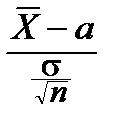 ~ N (0, 1).
~ N (0, 1).
Поэтому:
P 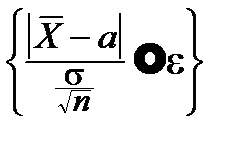 =F(e), "e>0.
=F(e), "e>0.
Заменим неравенство под знаком вероятности равносильным, разрешив его относительно a:
P {  -
- 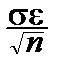 £ a £
£ a £  +
+ 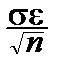 }=F(e)
}=F(e)
и можно сформулировать процедуру построения доверительного интервала для параметра a:
a) Задаём доверительную вероятность a.
b) По a с помощью таблицы функции Лапласа находим e из уравнения F(e)=a.
c) Искомый доверительный интервал имеет вид [  -
- 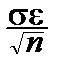 ,
,  +
+ 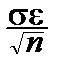 ],
],
Отметим, что длина доверительного интервала сколь угодно мала при больших n: 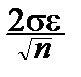
 0.
0.
3°. Доверительные интервалы для параметров нормального закона.
Пусть X ~ N (a, s) и оба параметра неизвестны. Воспользуемся следующей теоремой о выборочном среднем  и выборочной дисперсии S 2 для выборки из нормального закона:
и выборочной дисперсии S 2 для выборки из нормального закона:
a)  ~ N (a,
~ N (a, 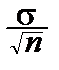 );
);
b)  nS 2~c
nS 2~c  ;
;
c) 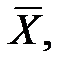 S 2 – независимые случайные величины;
S 2 – независимые случайные величины;
d) 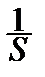 (
( - a)~ Tn -1.
- a)~ Tn -1.
Пункт a) этой теоремы очевиден, пункт d) следует из трёх предыдущих.
Действительно,
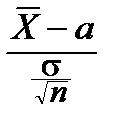 ~ N (0, 1);
~ N (0, 1); 
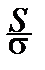 ~c n -1
~c n -1
и из независимости  и S следует, что отношение
и S следует, что отношение 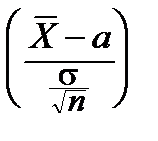 :
: 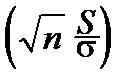 =
= 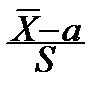 распределено по закону Стьюдента с (n -1) степенями свободы.
распределено по закону Стьюдента с (n -1) степенями свободы.
Пункты b) и c) примем без доказательства. Ограничимся только следующими замечаниями.
В выражении
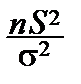 =
= 
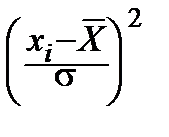
слагаемые – квадраты случайных величин 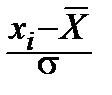 , распределённых по нормальному закону; если бы они были независимыми, то, как мы знаем, сумма была бы распределена по закону c n 2; однако они связаны линейной зависимостью:
, распределённых по нормальному закону; если бы они были независимыми, то, как мы знаем, сумма была бы распределена по закону c n 2; однако они связаны линейной зависимостью:

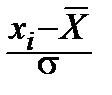 =0.
=0.
Оказывается, это влияет лишь на число степеней свободы у c2, понижая его на единицу. Можно вместо величин (x 1, x 2, ¼, xn) ввести с помощью линейного преобразования такие новые величины, которые остаются независимыми и нормальными, причем  и S 2 выражаются через различные новые переменные. Это и обеспечивает независимость. К тому же S 2 выражается через квадраты ровно (n -1) таких новых величин, что и приводит к c
и S 2 выражаются через различные новые переменные. Это и обеспечивает независимость. К тому же S 2 выражается через квадраты ровно (n -1) таких новых величин, что и приводит к c  . Осуществление этой программы мы здесь опустим.
. Осуществление этой программы мы здесь опустим.
Теперь построить доверительный интервал для a уже нетрудно:
P { 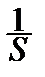 |
|  - a |£e}=2
- a |£e}=2 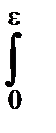 pTn -1(t) dt, "e>0,
pTn -1(t) dt, "e>0,
или
P {  -e S £ a £
-e S £ a £  +e S }=2
+e S }=2 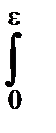 pTn -1(t) dt.
pTn -1(t) dt.
Строим доверительный интервал так:
a) Задаём a.
b) По a из таблицы распределения Стьюдента находим значение e из уравнения 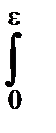 pTn -1(t) dt =
pTn -1(t) dt = 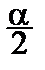 .
.
c) Нужный интервал имеет вид: [  -e S,
-e S,  +e S ].
+e S ].
Теорема о выборочном среднем позволяет построить доверительные интервалы также для s2и s. Действительно, так как  nS 2~c
nS 2~c  , то для любых x 1, x 2, таких, что 0£ x 1< x 2<+¥:
, то для любых x 1, x 2, таких, что 0£ x 1< x 2<+¥:
P { x 1£  nS 2£ x 2}=
nS 2£ x 2}= 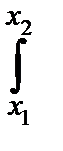
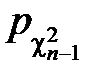 (x) dx.
(x) dx.
Перепишем неравенство под знаком вероятности, решив его относительно s2:
P {  £s2£
£s2£ 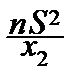 }=
}= 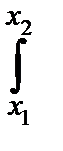
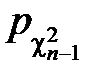 (x) dx.
(x) dx.
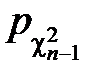 (x) (x)
|
|
Обычно выбирают x 1, и x 2так, чтобы заштрихованные на рисунке площади были равны. Если мы хотим построить интервал с доверительной вероятностью a, то величина каждой из этих площадей, очевидно, равна 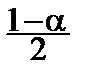 .
.
Процедура построения интервала:
a) Задаём a.
b) Находим x 1, и x 2по таблицам c2-распределения из уравнений:
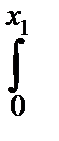
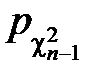 (x) dx =
(x) dx = 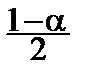 ,
, 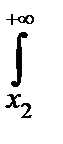
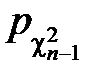 (x) dx =
(x) dx = 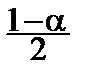 .
.
c) Вычисляем 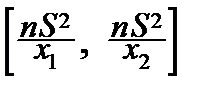 , что и решает нашу задачу.
, что и решает нашу задачу.
Очевидно, для параметра s доверительный интервал выглядит следующим образом:
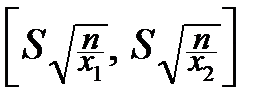 .
.



 ,
, 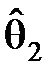 ], который с заданной вероятностью a накрывает неизвестный параметр q:
], который с заданной вероятностью a накрывает неизвестный параметр q: 0, тогда при достаточно большом числе наблюдений можно как угодно точно локализовать параметр q.
0, тогда при достаточно большом числе наблюдений можно как угодно точно локализовать параметр q. (x 1, x 2, ¼, xn) и хотя бы приближённо знаем закон её распределения. Именно в этом случае по закону распределения
(x 1, x 2, ¼, xn) и хотя бы приближённо знаем закон её распределения. Именно в этом случае по закону распределения  £ b }»
£ b }» 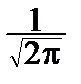
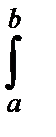
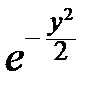 dy.
dy.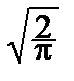
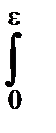
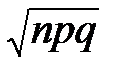 ).
). ~ N (a,
~ N (a, 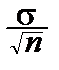 ). Его нормированное уклонение:
). Его нормированное уклонение: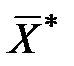 =
= 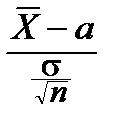 ~ N (0, 1).
~ N (0, 1).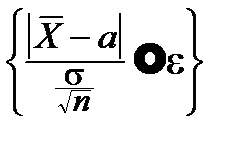 =F(e), "e>0.
=F(e), "e>0.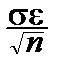 £ a £
£ a £ 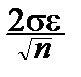
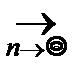 0.
0. nS 2~c
nS 2~c  ;
; S 2 – независимые случайные величины;
S 2 – независимые случайные величины;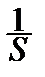 (
(
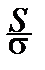 ~c n -1
~c n -1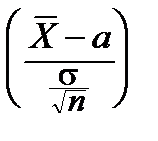 :
: 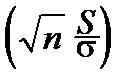 =
= 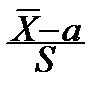 распределено по закону Стьюдента с (n -1) степенями свободы.
распределено по закону Стьюдента с (n -1) степенями свободы.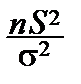 =
= 
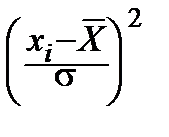
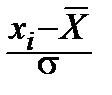 , распределённых по нормальному закону; если бы они были независимыми, то, как мы знаем, сумма была бы распределена по закону c n 2; однако они связаны линейной зависимостью:
, распределённых по нормальному закону; если бы они были независимыми, то, как мы знаем, сумма была бы распределена по закону c n 2; однако они связаны линейной зависимостью: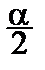 .
.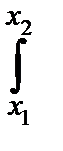
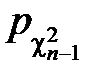 (x) dx.
(x) dx. £s2£
£s2£ 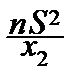 }=
}= 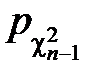 (x)
(x)
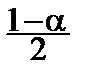 .
.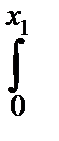
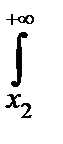
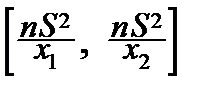 , что и решает нашу задачу.
, что и решает нашу задачу.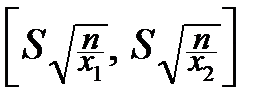 .
.

