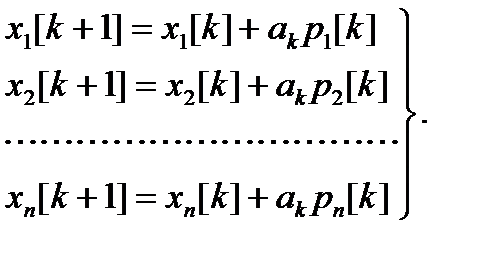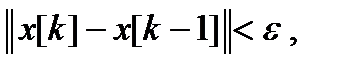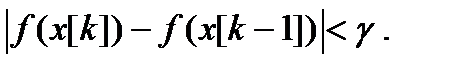Мы рассмотрели способ разностного представления дифференциального уравнения uxx = ut – формула (8.22). Граничные и начальные условия заданы в виде (8.20) и (8.21).
Способ, определяемый формулой (8.22), представляет собой явную систему уравнений для ui, j+1 в том же самом смысле, что и в случае гиперболического уравнения.
Имея на основании начальных и граничных условий первую строку решения, можно вычислить вторую строку, j = 1, непосредственно из (8.22).
Таким же способом можно продолжать вычислять решение столь далеко по оси времени, сколь в этом есть необходимость.
Процесс вычисления решения сходится и устойчив, если
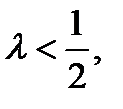
или, что то же самое, при
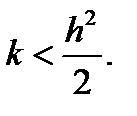
Тем самым накладываются довольно серьезные ограничения на выбор шага по времени, гораздо более серьезные, чем в случае гиперболического уравнения.
Именно это и заставляет искать возможности решения уравнения другими способами. Их трудоемкость гораздо больше, чем для явных формул (8.22), однако они устойчивы и сходятся для всех l > 0.
Тема 9
Методы безусловной оптимизации
9.0 Методы безусловной оптимизации. Введение
Решение многих теоретических и практических задач сводится к отысканию экстремума скалярной функции f (x) n -мерного векторного аргумента x.
Под x будем понимать вектор-столбец:
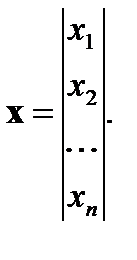
Вектор-строка получается путем транспонирования:
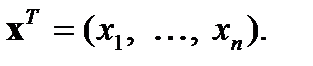
Оптимизируемую функцию f (x)называют целевой функцией, или критерием оптимальности.
В дальнейшем без ограничения общности будем говорить об отыскании минимума функции f (x)
f (x) → min.
Вектор x*, доставляющий минимум целевой функции, называют оптимальным.
Задачу максимизации можно заменить эквивалентной задачей минимизации и наоборот.
Рассмотрим это на примере функции одной переменной. Если x * – точка минимума функции
y = f (x), то для функции y = –f (x)она – точка максимума. Т. е. min f (x) = –max (– f (x)) (рис. 9.1).

|
| Рис. 9.1. Экстремумы
|
Сказанное справедливо и для функции многих переменных:
min (f (x1, …, xn )) = –max (– f (x1, …, xn )).
Так что далее речь будет идти только о минимизации.
Точка x * доставляет глобальный минимум функции одной переменной f (x), заданной на числовой прямой X, если x *Î X и f (x*) £ f (x) для всех x Î X.
Точка x * называется точкой строгого глобального минимума, если неравенство выполняется как строгое.
Если же в выражении f (x*) £ f (x) равенство возможно при x ¹ x *, то реализуется нестрогий минимум, а под решением понимают множество x * = { x Î X: f (x) = f (x*)} (рис. 9.2).

|
| Рис. 9.2. Глобальный минимум: а – строгий; б – нестрогий
|
Точка x * Î X доставляет локальный минимум функции f (x)на множестве X, если при некотором, достаточно малом e > 0 для всех x ¹ x*, x * Î X, удовлетворяющих условию
| x – x *| £ e, выполняется неравенство f (x*) £ f (x).
Если неравенство строгое, x * является точкой строгого локального минимума.
Все определения для максимумов функции получаются заменой знаков в неравенствах на обратные.
На рис. 9.3. показаны экстремумы функции одной переменной f (x) на отрезке [ a, b ].

|
| Рис. 9.3. Экстремумы функции. Точки x1, x3, x5 – локальные максимумы; точки x4, x6 – локальные минимумы; точка x2 – глобальный минимум; точка x7 – глобальный максимум
|
Проиллюстрируем трудности оптимизации на примере очень простых функций.
| Минимумы любого типа отсутствуют, когда функция не ограничена снизу
| f (x) = x
| 
|
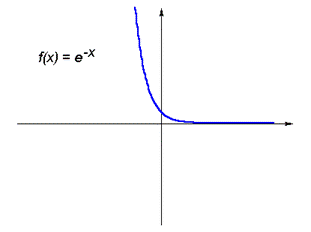
| Даже если она ограничена снизу, минимум может отсутствовать
| f (x) = e –x
| 
|
| Возможно бесконечное число локальных и глобальных минимумов
| f (x) = sin x
| 
|
| Возможно бесконечное число локальных и ни одного глобальногоминимума
| f (x) = x + 2 sin x
| 
|
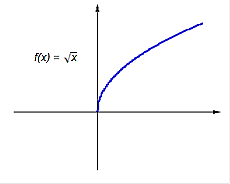
Если функция или ее производная разрывна, ситуации могут быть очень своеобразные: глобальный минимум есть, а локального нет!
В точке минимума производная 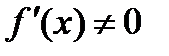 ! !
| 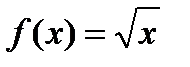
| 
|
В точке x = 0 производная 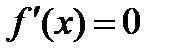 , а минимума нет , а минимума нет
| f (x) = x 3
| 
|
| Седловая точка функции двух переменных – по одной переменной достигнут максимум, по другой – минимум
| z (x, y) = x 2 – y 2
| 
|
9.1 Методы безусловной оптимизации. Классификация методов
Возможны два подхода для отыскания минимума функции многих переменных f (x) = f (x1, …, xn) при отсутствии ограничений на диапазон изменения неизвестных.
Первый подход лежит в основе косвенных методов оптимизации. Задача сводится к решению системы нелинейных уравнений. В точке экстремума x * все первые производные функции по независимым переменным обращаются в ноль:
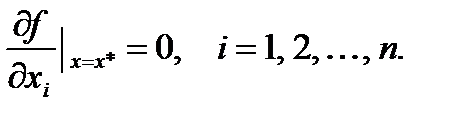
| (9.1)
|
Эти условия образуют систему из n нелинейных уравнений. Вектор 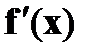 ,составленный из первых производных по каждой переменной, называют градиентом скалярной функции f (x). В точке минимума градиент равен 0.
,составленный из первых производных по каждой переменной, называют градиентом скалярной функции f (x). В точке минимума градиент равен 0.
Решение системы нелинейных уравнений – часто непростая задача. Поэтому на практике применялся иной подход. Он составляет основу прямых методов оптимизации.
Идея подхода: построение последовательности векторов x [ 0 ], x [ 1 ], …, x [ n ], …, таких что f (x [0]) > f (x [1]) >…> f (x [ n ]) > ….
Здесь [ i ] нумерует точки (и итерации).
Точку x [0] выбираем произвольно, но лучше недалеко от минимума.
Переход (итерация) от точки x [ k ] к точке x [ k + 1] (k = 0, 1, 2, …) состоит из двух этапов:
1) выбор направления движения;
2) определение шага вдоль выбранного направления.
Методы построения таких последовательностей называют методами спуска – переход от бóльших значений функции к меньшим.
Методы спуска описываются так:
x [ k+1 ] = x [ k ] + a k p [ k ], k = 0, 1, 2, …,
где p [ k ] – вектор, определяющий направление спуска; a k – длина шага.
В координатной форме:
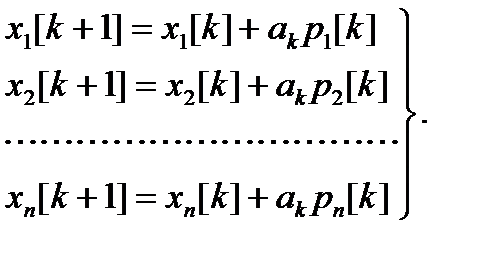
Разные методы спуска отличаются разными способами выбора параметров (направления и шага).
Метод должен сходиться – за конечное число шагов надо найти минимум или приблизиться к нему. Качество методов оценивают по скорости сходимости.
Критерии останова итераций либо малость приращения аргумента или функции:
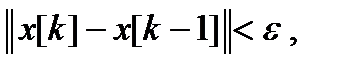
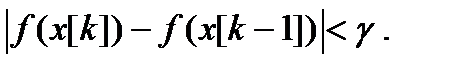
Здесь k – номер итерации; e, g – заданные величины точности.
Метод поиска детерминирован, если оба параметра (направление и шаг) для перехода от x [ k ] к x [ k + 1 ] выбираются однозначно, по доступной в точке x [ k ] информации.
Если при переходе применяется механизм случайного выбора, алгоритм называется случайным поиском минимума.
Детерминированные алгоритмы делят на классы в зависимости от вида используемой информации.
Если на каждой итерации используется
• лишь значение функции – это методы нулевого порядка;
• если плюс к этому надо вычислять первые производные от минимизируемой функции – методы первого порядка;
• если плюс к этому надо вычислять вторые производные от минимизируемой функции – методы второго порядка.
Характеристики качества метода:
• скорость сходимости;
• время выполнения одной итерации;
• объем ОЗУ, нужный для решения задачи;
• класс решаемых задач и др.
Задачи могут иметь малую или большую размерность, быть унимодальными или многоэкстремальными и т. д.
Как правило, имеющиеся методы не универсальны. Выбор – исходя из специфики задачи.
9.2 Методы безусловной оптимизации нулевого порядка



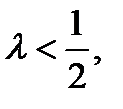
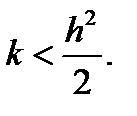

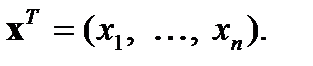

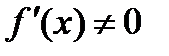 !
!
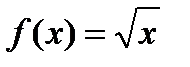

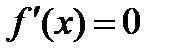 , а минимума нет
, а минимума нет
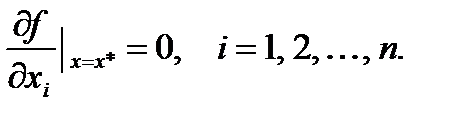
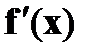 ,составленный из первых производных по каждой переменной, называют градиентом скалярной функции f (x). В точке минимума градиент равен 0.
,составленный из первых производных по каждой переменной, называют градиентом скалярной функции f (x). В точке минимума градиент равен 0.