Полагая в формуле Грина Q=x, P=0, а затем Q=0, P= -y и учитывая, что  (по G), где S – площадь области G, получим выражения для площади области через криволинейные интегралы по её границе: S =
(по G), где S – площадь области G, получим выражения для площади области через криволинейные интегралы по её границе: S =  (по L), S = -
(по L), S = -  (по L).
(по L).
Пусть α и β — произвольные числа такие, что α +β=1. Умножая равенства на α и β и складывая, получим еще одну формулу для площади: S =  (по L).
(по L).
Формула Стокса
Если функции  дифференцируемы в области
дифференцируемы в области  и в этой области расположен некоторый замкнутый контур
и в этой области расположен некоторый замкнутый контур  , то для любой незамкнутой поверхности
, то для любой незамкнутой поверхности  , имеющей границу
, имеющей границу  , имеет место формула Стокса:
, имеет место формула Стокса:
 ,
,
где на 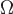 берется та сторона, в точках которой вектор нормали
берется та сторона, в точках которой вектор нормали  направлен так, чтобы видимый с его конца обход контура
направлен так, чтобы видимый с его конца обход контура  совершался бы против часовой стрелки (ориентация поверхности согласована с обходом контура).
совершался бы против часовой стрелки (ориентация поверхности согласована с обходом контура).
Формула Стокса позволяет свести вычисление циркуляции векторного поля  по контуру
по контуру  к вычислению потока поля
к вычислению потока поля  через незамкнутую поверхность
через незамкнутую поверхность 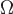 , опирающуюся на контур
, опирающуюся на контур  (здесь
(здесь  – граница незамкнутой поверхности
– граница незамкнутой поверхности 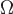 ). Заметим, что
). Заметим, что 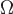 – любая поверхность, имеющая границей контур
– любая поверхность, имеющая границей контур  , поэтому возможен наиболее простой ее выбор.
, поэтому возможен наиболее простой ее выбор.
Если через контур  провести две поверхности
провести две поверхности  и
и 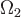 , то
, то
 .
.
Учитывая, что  и
и 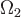 ограничивают некоторую пространственное тело
ограничивают некоторую пространственное тело  и, меняя направление нормали на поверхности
и, меняя направление нормали на поверхности 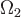 на противоположное, т.е. на внешнее по отношению к
на противоположное, т.е. на внешнее по отношению к  , получим
, получим
 ,
,
т. е. поток вихря через замкнутую поверхность равен. Это означает, что поле вихря является соленоидальным.
44. Вихрь векторного поля его свойства.
 Пусть векторное поле образовано вектором
Пусть векторное поле образовано вектором  .
.
Возьмем в этом поле некоторую замкнутую кривую L и выберем на ней определенное направление (рис. 32).
Циркуляцией вектора  вдоль кривой
вдоль кривой  , называется криволинейный интеграл по замкнутому контуру от вектор - функции
, называется криволинейный интеграл по замкнутому контуру от вектор - функции  .
.
Ц =

Другое обозначение Ц =  (
( ,
,  - скалярное произведение)
- скалярное произведение)
Физический смысл циркуляции: если кривая L расположена в силовом поле, то циркуляция – это работа силы  поля при перемещении материальной точки вдоль контура L.
поля при перемещении материальной точки вдоль контура L.
Циркуляция поля по данному контуру характеризует вращательную способность поля на данном контуре.
При этом важно заметить, что циркуляция данного поля зависит не только от формы контура, но и от его ориентации в пространстве.
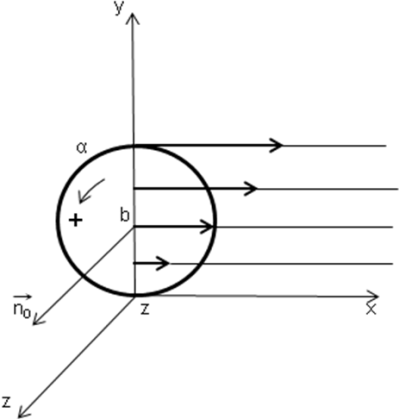
Пример:
Найти циркуляцию поля  по контуру окружности
по контуру окружности  , расположенной в плоскости Оху (рис. 33).
, расположенной в плоскости Оху (рис. 33).

(знак минус указывает на то, что контур в данном поле будет вращаться в направлении, противоположном принятому за положительное.)
Если этот же контур поместить в поле этого вектора, но в плоскости параллельной плоскости Оxz, то вектор  в любой точке плоскости будет иметь одно и тоже значение, циркуляция будет равна нулю.
в любой точке плоскости будет иметь одно и тоже значение, циркуляция будет равна нулю.
Ротором (или вихрем) векторного поля  называется вектор, определяемый формулой
называется вектор, определяемый формулой

В символическом виде

Направление ротора - это направление, вокруг которого циркуляция имеет наибольшее значение по сравнению с циркуляцией вокруг любого другого направления.
Связь между ротором и циркуляцией аналогична связи между градиентом и производной по направлению.



 дифференцируемы в области
дифференцируемы в области  и в этой области расположен некоторый замкнутый контур
и в этой области расположен некоторый замкнутый контур  , то для любой незамкнутой поверхности
, то для любой незамкнутой поверхности  , имеющей границу
, имеющей границу  ,
,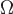 берется та сторона, в точках которой вектор нормали
берется та сторона, в точках которой вектор нормали  направлен так, чтобы видимый с его конца обход контура
направлен так, чтобы видимый с его конца обход контура  по контуру
по контуру  через незамкнутую поверхность
через незамкнутую поверхность  и
и 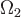 , то
, то .
. ,
, Пусть векторное поле образовано вектором
Пусть векторное поле образовано вектором  .
. вдоль кривой
вдоль кривой  , называется криволинейный интеграл по замкнутому контуру от вектор - функции
, называется криволинейный интеграл по замкнутому контуру от вектор - функции  .
.
 (
( ,
,  - скалярное произведение)
- скалярное произведение) поля при перемещении материальной точки вдоль контура L.
поля при перемещении материальной точки вдоль контура L.
 по контуру окружности
по контуру окружности  , расположенной в плоскости Оху (рис. 33).
, расположенной в плоскости Оху (рис. 33).
 в любой точке плоскости будет иметь одно и тоже значение, циркуляция будет равна нулю.
в любой точке плоскости будет иметь одно и тоже значение, циркуляция будет равна нулю.




