До цих пір розглядали підмножини із скінченних множин, що складаються з різних елементів. Часто на практиці мають місце випадки, коли серед розглянутих елементів є однакові. Тому вводять три типа аналогічних комбінаторних з'єднань, але з елементами, що поможуть повторюватися:
1) перестановки із повтореннями елементів;
2) розміщення із повтореннями елементів;
3) сполучення із повтореннями елементів.
Перестановки із повторенням елементів
Дана множина 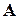 , що складається із
, що складається із  елементів, у якій:
елементів, у якій:
– 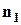 елемент належить першому типу;
елемент належить першому типу;
– 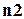 елементів належить другого типу елементів; ;
елементів належить другого типу елементів; ;
... ;
– 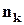 елементів належить
елементів належить 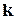 -тому типу елементів.
-тому типу елементів.
Елементи одного й того ж типу не розрізняються між собою.
Специфікацією множини 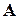 називається набір
називається набір 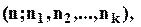
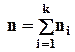 .
.
Теорема 1

Доведення.
Нехай 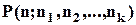 – число різних перестановок з повтореннями у множині
– число різних перестановок з повтореннями у множині 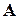 . Якщо б всі елементи множини
. Якщо б всі елементи множини 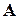 були різні, то їх можна було б переставити
були різні, то їх можна було б переставити 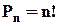 способами.
способами.
Число 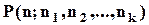 менше за
менше за 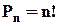 у
у 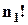 разів саме за рахунок перестановок елементів першого типу, у
разів саме за рахунок перестановок елементів першого типу, у 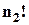 – за рахунок елементів 2 типу, та, ..., у
– за рахунок елементів 2 типу, та, ..., у 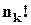 – за рахунок елементів
– за рахунок елементів 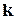 -того типу.
-того типу.
Слідство
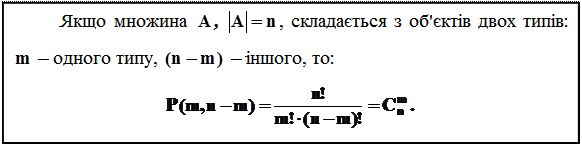
У загальному випадку:
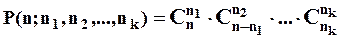
Наприклад.
1) Скількома способами можна переставити букви в слові "каша"?
Розв’язання.
Усього в слові "каша" чотири літери, серед яких дві однакові:
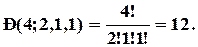
2) Скільки різних чисел можна отримати, переставляючи цифри числа 12341234?
Розв’язання.
У числі 8 цифр: дві – "1", дві – "2", дві – "3", дві – "4". За теоремою 1 маємо:
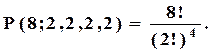
3) Скільки різних перестановок можна утворити з усіх літер слова «Міссісіпі»?
Розв’язання.
Всього в слові 9 букв, з них – 4 літери "і", три літери "с", одна літера "м" та одна літера "п".
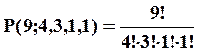 .
.
4) Тридцять осіб розбиті на 3 групи по 10 чоловік у кожній. Скільки різних складів груп можна скласти?
Розв’язання.
Задача може бути розв’язана двома способами, що випливає із слідства до теореми про перестановки із повтореннями.
Порядок входження людей до груп не має значення. Тоді, спочатку, вибираємо десять чоловік із тридцяти, що увійдуть у першу групу. Це можна зробити 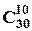 способами. Потім, із двадцяти тих, що лишилися, вибираємо десять чоловік для другої групи, й останні десять складуть третю групу. За правилом добутку, маємо:
способами. Потім, із двадцяти тих, що лишилися, вибираємо десять чоловік для другої групи, й останні десять складуть третю групу. За правилом добутку, маємо:
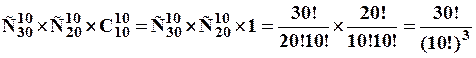 .
.
Другий спосіб слідкує із безпосереднього застосування логіки теореми про перестановки із повтореннями. Розбиття тридцяти чоловік на три групи можна отримати наступним чином. Взяти усі перестановки тридцяти чоловік: 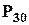 та виключити з них перестановки перших десяти:
та виключити з них перестановки перших десяти: 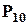 , бо вони усі увійдуть у першу групу і перестановки їх між собою враховувати не треба (тобто вони в цьому сенсі вважаються однаковими). Потім аналогічно, виключити перестановки другої десятки та третьої. Тоді, кількість перестановок із повтореннями із специфікацією
, бо вони усі увійдуть у першу групу і перестановки їх між собою враховувати не треба (тобто вони в цьому сенсі вважаються однаковими). Потім аналогічно, виключити перестановки другої десятки та третьої. Тоді, кількість перестановок із повтореннями із специфікацією 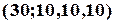 дорівнює:
дорівнює:
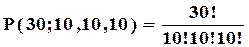 .
.
Розміщення з повтореннями
(  -перестановки з необмеженими повтореннями)
-перестановки з необмеженими повтореннями)
Нехай 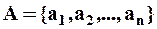 – множина типів елементів,
– множина типів елементів, 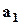 – "представник" першого типу елементів,
– "представник" першого типу елементів, 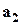 – другого типу, ...,
– другого типу, ..., 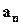 –
–  -того типу елементів. Елементів кожного типу є в необмеженій кількості, елементи одного типу нерозрізнені між собою.
-того типу елементів. Елементів кожного типу є в необмеженій кількості, елементи одного типу нерозрізнені між собою.
Розміщення із повтореннями з  по
по  – упорядкована послідовність довжиною
– упорядкована послідовність довжиною  така, що:
така, що:
– кожен елемент послідовності одного із  типів;
типів;
– не усі елементи послідовності обов'язково різні.
Наприклад.
Згенерувати усі розміщення із повтореннями елементів з 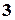 по
по 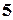 у множині
у множині 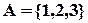 . Розміщення розташовані у порядку зростання натурального числа поставленого у відповідність кожному розміщенню.
. Розміщення розташовані у порядку зростання натурального числа поставленого у відповідність кожному розміщенню.
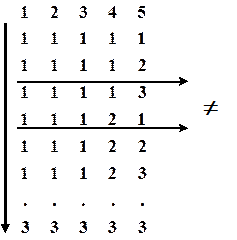
Теорема 2

Доведення.
Розглянемо наступну схему вибору упорядкованої послідовності довжиною у  елементів: нехай маємо нескінченну кількість елементів кожного із
елементів: нехай маємо нескінченну кількість елементів кожного із  типів (наприклад, кулі із наклеєними номерами) та
типів (наприклад, кулі із наклеєними номерами) та  різних, перенумерованих, місць або комірок, які треба заповнити цими елементами. Вибираємо елемент на перше місце, є
різних, перенумерованих, місць або комірок, які треба заповнити цими елементами. Вибираємо елемент на перше місце, є  варіантів вибору. На друге місце після цього і незалежно від того, елемент якого типу вже був обраний, є також
варіантів вибору. На друге місце після цього і незалежно від того, елемент якого типу вже був обраний, є також  претендентів. І так далі, відповідно, на
претендентів. І так далі, відповідно, на  місце є, як і раніше,
місце є, як і раніше,  претендентів. За правилом добутку маємо:
претендентів. За правилом добутку маємо:
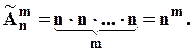
Зауваження: у цьому випадку може бути 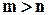 .
.
Наприклад. Скільки різних наборів сигналів можуть дати чотири світлофора одночасно?
Розв’язання.
Кожен із світлофорів незалежно від інших може давати 3 варіанти сигналів: зелений, жовтий та червоний, тобто число типів елементів, що повторюються, дорівнює трійці. Довжина упорядкованої послідовності – це кількість світлофорів. Світлофори різні (розташовані у різних місцях) тому має значення, на якому світлофорі горить який сигнал, тобто послідовність повинна бути упорядкована. Тоді маємо: 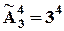 .
.
Сполучення з повтореннями
Нехай 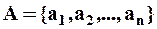 – множина типів елементів,
– множина типів елементів, 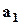 – "представник" першого типу елементів,
– "представник" першого типу елементів, 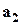 – "представник" другого типу, ...,
– "представник" другого типу, ..., 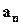 –
–  -того типу елементів.
-того типу елементів.
Елементів кожного типу є в необмеженій кількості, елементи одного типу нерозрізнені між собою.
Сполучення із повтореннями з  по
по  – неупорядкована послідовність довжиною
– неупорядкована послідовність довжиною  така, що:
така, що:
– кожен елемент послідовності одного з  типів;
типів;
– не всі елементи послідовності обов'язково різні.
Сполучення із повтореннями відрізняються один від одного складом елементів, що входять до сполучення, порядок елементів не має значення. Має значення, скільки елементів кожного типу увійшло до сполучення.
Наприклад.
Згенерувати всі сполучення із повтореннями елементів із 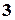 по
по 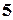 у множині
у множині 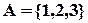 . Сполучення розташовані у порядку зростання натурального числа поставленого у відповідність кожному сполученню.
. Сполучення розташовані у порядку зростання натурального числа поставленого у відповідність кожному сполученню.
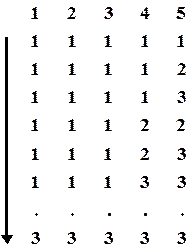
Теорема 3
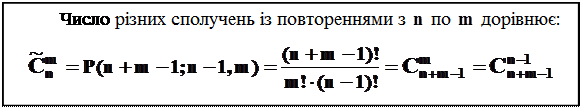
Доведення.
Розглянемо певне сполучення. Нехай у нього входять 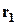 об'єкт першого типу,
об'єкт першого типу, 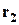 об'єктів другого типу,
об'єктів другого типу, 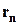 об'єктів
об'єктів  -го типу, причому
-го типу, причому 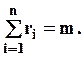
Деякі 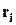 можуть бути рівними нулю. Кожному сполученню можна поставити у взаємно-однозначну відповідність наступну схему:
можуть бути рівними нулю. Кожному сполученню можна поставити у взаємно-однозначну відповідність наступну схему:
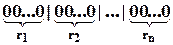 .
.
Елементи, що становлять сполучення, кодуються нулями, їх всього  . Вертикальні риски відокремлюють елементи одного типу від елементів іншого типу. Якщо елементи будь-якого виду немає, дві риски будуть стояти поспіль. Кількість рисок дорівнює
. Вертикальні риски відокремлюють елементи одного типу від елементів іншого типу. Якщо елементи будь-якого виду немає, дві риски будуть стояти поспіль. Кількість рисок дорівнює 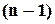 . Кожному сполученню із повтореннями відповідає схема і навпаки, кожна подібна схема відповідає деякому сполученню із повтореннями, тобто між ними існує взаємно-однозначна відповідність або бієкція. Тоді, кількість сполучень із повтореннями з
. Кожному сполученню із повтореннями відповідає схема і навпаки, кожна подібна схема відповідає деякому сполученню із повтореннями, тобто між ними існує взаємно-однозначна відповідність або бієкція. Тоді, кількість сполучень із повтореннями з  по
по  дорівнює числу таких схем.
дорівнює числу таких схем.
Підрахуємо кількість різних таких схем. Усього в схемі 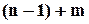 об'єктів:
об'єктів: 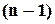 риска та
риска та  нулів. Число схем дорівнює кількості різних перестановок з
нулів. Число схем дорівнює кількості різних перестановок з 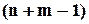 елементів, серед яких
елементів, серед яких 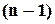 однакових "|" та
однакових "|" та  однакових "0". За теоремою про перестановки із повтореннями для множини елементів із специфікацією
однакових "0". За теоремою про перестановки із повтореннями для множини елементів із специфікацією 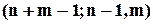 маємо, що число таких схем, а відповідно й число сполучень із повтореннями із
маємо, що число таких схем, а відповідно й число сполучень із повтореннями із  по
по  складає:
складає: 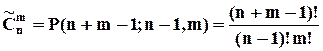 .
.
З другого боку, права частина цієї рівності може бути записана як кількість звичайних сполучень без повторень елементів із 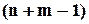 елементів по
елементів по  :
: 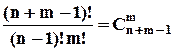 , або із урахуванням властивості симетричність для сполучень:
, або із урахуванням властивості симетричність для сполучень: 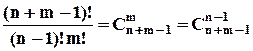 .
.
Таким чином доведено, що справедливі співвідношення:
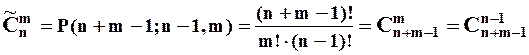 .
.
Наприклад.
1) У кондитерській продають 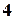 типи тістечок. Скількома способами одна людина може купити
типи тістечок. Скількома способами одна людина може купити 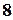 тістечок?
тістечок?
Розв’язання.
Оскільки тістечка купує одна людина, то не має значення у якому порядку вона їх вибирає, а враховується тільки склад купівлі, тобто скільки тістечок якого типу було вибрано. Кількість типів тістечок дорівнює 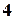 , кількість тістечок, що куплено в свою чергу дорівнює
, кількість тістечок, що куплено в свою чергу дорівнює 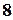 . Вважається, що кожного типу тістечок мається стільки, скільки потрібно. Тоді, за теоремою про сполучення із повтореннями маємо:
. Вважається, що кожного типу тістечок мається стільки, скільки потрібно. Тоді, за теоремою про сполучення із повтореннями маємо:
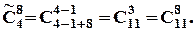
2) У кондитерській продають 4 типи тістечок. Скількома способами 8 різних людей можуть купити по одному тістечку?
Розв’язання.
Для даної задачі, має значення не тільки склад, а й порядок здійснення купівлі, бо тістечка отримують різні люди. Перше куплене тістечко отримає перша людина, друге – друга, і так далі. Кількість типів тістечок дорівнює 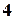 , кількість тістечок, що куплено в свою чергу дорівнює
, кількість тістечок, що куплено в свою чергу дорівнює 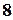 . Також вважається, що кожного типу тістечок мається стільки, скільки потрібно. Тому за теоремою про розміщення із повтореннями маємо:
. Також вважається, що кожного типу тістечок мається стільки, скільки потрібно. Тому за теоремою про розміщення із повтореннями маємо: 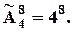
3) Знайти кількість різних способів, якими можна виписати в один ряд 6 плюсів та 4 мінуса?
Розв’язання.
Усього маємо десять символів, серед яких шість однакових плюсів та чотири однакові мінуси. Тому за теоремою про перестановки із повтореннями маємо:
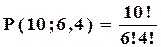 .
.
З другого боку, маємо десять місць, на які потрібно розташувати описані символи. Спочатку вибираємо шість місць для розташування плюсів, це 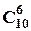 способів, а потім на ті місця, що осталися, а їх чотири. розміщуємо мінуси. Оскільки усі плюси та мінуси між собою не відрізняються, то маємо:
способів, а потім на ті місця, що осталися, а їх чотири. розміщуємо мінуси. Оскільки усі плюси та мінуси між собою не відрізняються, то маємо:
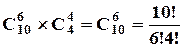 .
.
3) Знайти число способів виписати в один ряд 9 трійок та 6 п'ятірок так, щоб ніякі дві п'ятірки не стояли поруч?
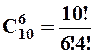 .
.
4) Скількома способами можна переставити букви в слові "каракулі", щоб ніякі дві голосні не стояли поруч?
Розв’язання.
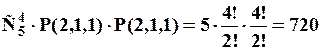 .
.
5) 30 чоловік голосують по п'ятьом кандидатам на пост голови наукового товариства. Скількома способами можуть розподілитися голоси, якщо враховується тільки кількість голосів поданих за кожного кандидата?
Скількома способами можуть розподілитися голоси, якщо враховується тільки кількість голосів поданих за кожного кандидата і за кожного поданий хоча б 1 голос?
Розв’язання.
Перша задача є стандартна задача про сполучення із повтореннями, бо за постановкою задачі не має значення, хто за кого проголосував, а враховується тільки кількість голосів, поданих за кожного кандидата:
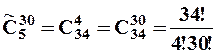 .
.
Друга задача може бути розв’язана двома способами. По-перше, відомо, що за кожного кандидата був поданий один голос, тобто п’ять чоловіків вже проголосували. Зосталося врахувати, як розподілилися голоси 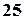 чоловік, що осталися. У такій постановці задача зводиться до стандартної задачі про сполучення із повтореннями, але вже для
чоловік, що осталися. У такій постановці задача зводиться до стандартної задачі про сполучення із повтореннями, але вже для 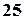 чоловік:
чоловік:
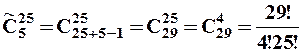 .
.
По-друге, задача може бути вирішена за допомогою схеми, що використовувалась при доведенні теореми про сполучення із повтореннями. Усі 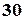 чоловік кодуємо нулями, а для того, щоб відділити, скільки чоловік проголосувало за якого кандидата, ставимо риски. Але тепер риска не може стояти до послідовності нулів (за першого кандидата ніхто не проголосував), після неї (за останнього кандидата ніхто не проголосував) та дві риски не можуть йти поспіль (за якогось кандидата не буде подано ні одного голосу). Тоді, щоб розставити риски існує
чоловік кодуємо нулями, а для того, щоб відділити, скільки чоловік проголосувало за якого кандидата, ставимо риски. Але тепер риска не може стояти до послідовності нулів (за першого кандидата ніхто не проголосував), після неї (за останнього кандидата ніхто не проголосував) та дві риски не можуть йти поспіль (за якогось кандидата не буде подано ні одного голосу). Тоді, щоб розставити риски існує 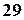 місць, по одному між кожними двома із
місць, по одному між кожними двома із 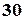 нулів. Всього треба поставити чотири риски, тому маємо:
нулів. Всього треба поставити чотири риски, тому маємо: 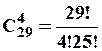 .
.
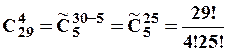 ,
, 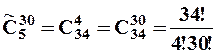 .
.



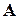 , що складається із
, що складається із  елементів, у якій:
елементів, у якій: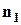 елемент належить першому типу;
елемент належить першому типу;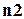 елементів належить другого типу елементів; ;
елементів належить другого типу елементів; ;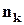 елементів належить
елементів належить 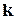 -тому типу елементів.
-тому типу елементів.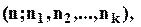
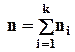 .
.
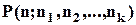 – число різних перестановок з повтореннями у множині
– число різних перестановок з повтореннями у множині 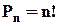 способами.
способами.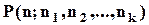 менше за
менше за 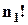 разів саме за рахунок перестановок елементів першого типу, у
разів саме за рахунок перестановок елементів першого типу, у 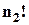 – за рахунок елементів 2 типу, та, ..., у
– за рахунок елементів 2 типу, та, ..., у 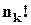 – за рахунок елементів
– за рахунок елементів 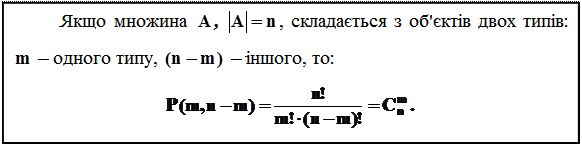
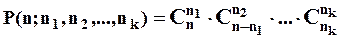
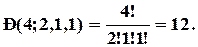
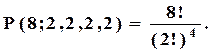
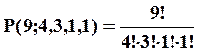 .
.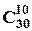 способами. Потім, із двадцяти тих, що лишилися, вибираємо десять чоловік для другої групи, й останні десять складуть третю групу. За правилом добутку, маємо:
способами. Потім, із двадцяти тих, що лишилися, вибираємо десять чоловік для другої групи, й останні десять складуть третю групу. За правилом добутку, маємо: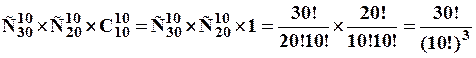 .
.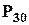 та виключити з них перестановки перших десяти:
та виключити з них перестановки перших десяти: 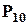 , бо вони усі увійдуть у першу групу і перестановки їх між собою враховувати не треба (тобто вони в цьому сенсі вважаються однаковими). Потім аналогічно, виключити перестановки другої десятки та третьої. Тоді, кількість перестановок із повтореннями із специфікацією
, бо вони усі увійдуть у першу групу і перестановки їх між собою враховувати не треба (тобто вони в цьому сенсі вважаються однаковими). Потім аналогічно, виключити перестановки другої десятки та третьої. Тоді, кількість перестановок із повтореннями із специфікацією 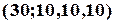 дорівнює:
дорівнює: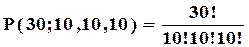 .
. -перестановки з необмеженими повтореннями)
-перестановки з необмеженими повтореннями)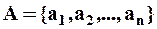 – множина типів елементів,
– множина типів елементів, 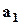 – "представник" першого типу елементів,
– "представник" першого типу елементів, 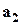 – другого типу, ...,
– другого типу, ..., 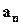 –
– 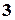 по
по 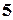 у множині
у множині 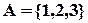 . Розміщення розташовані у порядку зростання натурального числа поставленого у відповідність кожному розміщенню.
. Розміщення розташовані у порядку зростання натурального числа поставленого у відповідність кожному розміщенню.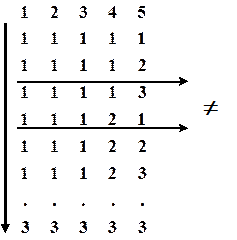

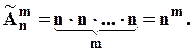
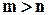 .
.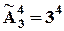 .
.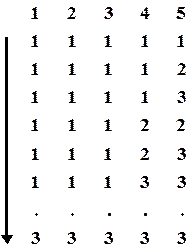
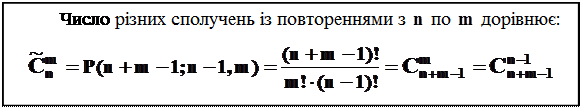
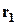 об'єкт першого типу,
об'єкт першого типу, 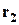 об'єктів другого типу,
об'єктів другого типу, 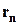 об'єктів
об'єктів 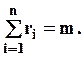
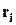 можуть бути рівними нулю. Кожному сполученню можна поставити у взаємно-однозначну відповідність наступну схему:
можуть бути рівними нулю. Кожному сполученню можна поставити у взаємно-однозначну відповідність наступну схему: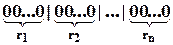 .
.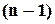 . Кожному сполученню із повтореннями відповідає схема і навпаки, кожна подібна схема відповідає деякому сполученню із повтореннями, тобто між ними існує взаємно-однозначна відповідність або бієкція. Тоді, кількість сполучень із повтореннями з
. Кожному сполученню із повтореннями відповідає схема і навпаки, кожна подібна схема відповідає деякому сполученню із повтореннями, тобто між ними існує взаємно-однозначна відповідність або бієкція. Тоді, кількість сполучень із повтореннями з 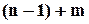 об'єктів:
об'єктів: 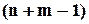 елементів, серед яких
елементів, серед яких 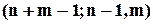 маємо, що число таких схем, а відповідно й число сполучень із повтореннями із
маємо, що число таких схем, а відповідно й число сполучень із повтореннями із 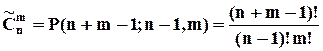 .
.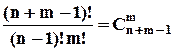 , або із урахуванням властивості симетричність для сполучень:
, або із урахуванням властивості симетричність для сполучень: 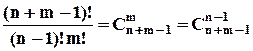 .
.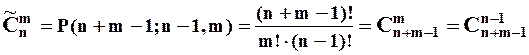 .
.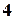 типи тістечок. Скількома способами одна людина може купити
типи тістечок. Скількома способами одна людина може купити 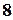 тістечок?
тістечок?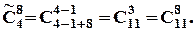
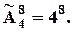
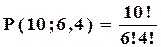 .
.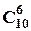 способів, а потім на ті місця, що осталися, а їх чотири. розміщуємо мінуси. Оскільки усі плюси та мінуси між собою не відрізняються, то маємо:
способів, а потім на ті місця, що осталися, а їх чотири. розміщуємо мінуси. Оскільки усі плюси та мінуси між собою не відрізняються, то маємо: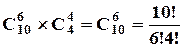 .
.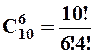 .
.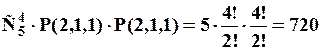 .
.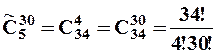 .
.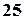 чоловік, що осталися. У такій постановці задача зводиться до стандартної задачі про сполучення із повтореннями, але вже для
чоловік, що осталися. У такій постановці задача зводиться до стандартної задачі про сполучення із повтореннями, але вже для 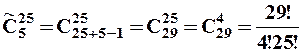 .
.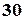 чоловік кодуємо нулями, а для того, щоб відділити, скільки чоловік проголосувало за якого кандидата, ставимо риски. Але тепер риска не може стояти до послідовності нулів (за першого кандидата ніхто не проголосував), після неї (за останнього кандидата ніхто не проголосував) та дві риски не можуть йти поспіль (за якогось кандидата не буде подано ні одного голосу). Тоді, щоб розставити риски існує
чоловік кодуємо нулями, а для того, щоб відділити, скільки чоловік проголосувало за якого кандидата, ставимо риски. Але тепер риска не може стояти до послідовності нулів (за першого кандидата ніхто не проголосував), після неї (за останнього кандидата ніхто не проголосував) та дві риски не можуть йти поспіль (за якогось кандидата не буде подано ні одного голосу). Тоді, щоб розставити риски існує 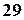 місць, по одному між кожними двома із
місць, по одному між кожними двома із 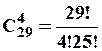 .
.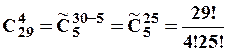 ,
, 


