МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ДЕРЖАВНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД
«ДОНЕЦЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ»
КАФЕДРА ПРИКЛАДНОЇ МАТЕМАТИКИ І ІНФОРМАТИКИ

МЕТОДИЧНІ ВКАЗІВКИ ТА ЗАВДАННЯ
До самостійної роботи та виконання індивідуального завдання за курсом
«ОДМ, частина 1»
Донецьк-2010
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ДЕРЖАВНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД
«ДОНЕЦЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ»
КАФЕДРА ПРИКЛАДНОЇ МАТЕМАТИКИ І ІНФОРМАТИКИ
МЕТОДИЧНІ ВКАЗІВКИ ТА ЗАВДАННЯ
До самостійної роботи та виконання індивідуального завдання за курсом
«ОДМ, частина 1»
Для студентів, що навчаються за напрямом підготовки
« Комп’ютерні науки»
Розглянуто на засіданні кафедри
прикладної математики і інформатики
протокол № 11 від 17.05.2010
Затверджено на засіданні
навчально-видавничої ради ДонНТУ
протокол № від . .
Донецьк-2010
УДК 004.021
Методичні вказівки та завдання до самостійної роботи та виконання індивідуального завдання за курсом "ОДМ, частина 1" (для студентів, що навчаються за напрямом підготовки "Комп’ютерні науки ") / Укл.: І.А. Назарова. - Донецьк: ДонНТУ, 2010. - 48с.
Методичні вказівки містять теоретичні матеріали, завдання та приклади розв’язання задач із одного із «Комбінаторного аналізу» - найважливіших розділів курсу “ Основи дискретної математики”.
Укладач: Назарова І.А., к.т.н., доцент
Рецензент Скобцов Ю.О., д.т.н., професор
Вступ
Комбінаторика – розділ математики, що вивчає різні співвідношення між елементами, як правило, скінченних множин.
Основні типи задач
1) Задачі переліку (скільки?):
визначення кількості елементів множини, що володіють заданими властивостями.
2) Задачі генерації або перелічення (які?):
формування списків елементів множини, що володіють заданими властивостями.
3) Задачі комбінаторної оптимізації:
визначення підмножини деякої множини елементів, на якому задана функція приймає мінімальне або максимальне значення.
Правила суми та добутку
Важливу роль при розв’язанні багатьох найбільш простих комбінаторних задач грають правила суми та добутку. Сформулюємо ці правила з точки зору комбінаторики для двомірного випадку.
Правило суми
Якщо об'єкт 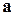 може бути вибраний
може бути вибраний  способами, а об'єкт
способами, а об'єкт 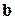 –
–  іншими способами, то вибір "
іншими способами, то вибір " 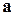 або
або 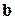 " може бути здійснено
" може бути здійснено 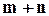 способами.
способами.
Вибір 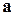 і
і 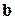 – є взаємовиключним: вибір об'єкта
– є взаємовиключним: вибір об'єкта 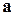 виключає вибір об'єкта
виключає вибір об'єкта 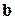 ; жоден спосіб вибору об'єкта
; жоден спосіб вибору об'єкта 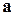 не збігається із жодним способом вибору об'єкта
не збігається із жодним способом вибору об'єкта 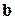 .
.
Наприклад.
З Києва до Донецька протягом доби відправляється три потяга та один літак. Скільки існує способів виїхати із Києва до Донецька?
Розв’язання.
З Києва до Донецька можна доїхати або потягом, або літаком. Ніякий спосіб їхати потягом не співпадає ні з яким способом, якщо вибрано літак. Якщо летимо, то не їдемо потягом, якщо їдемо потягом, то не летимо, тобто вибір є взаємовиключним. Маємо змогу застосувати правило суми. За правилом суми: 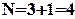 .
.
Правило добутку
Якщо об'єкт 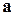 може бути вибраний
може бути вибраний  способами, і після цього, і незалежно від цього об'єкт
способами, і після цього, і незалежно від цього об'єкт 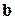 може бути вибраний
може бути вибраний  способами, то вибір "
способами, то вибір " 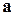 та
та 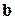 " може бути здійснено
" може бути здійснено 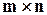 способами.
способами.
Вибір " 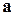 та
та 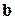 " – незалежний: вибір об'єкта
" – незалежний: вибір об'єкта 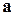 не впливає на кількість способів вибору об'єкта
не впливає на кількість способів вибору об'єкта 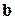 .
.
Зауваження: правила суми та добутку можуть бути поширені на  - мірний випадок.
- мірний випадок.
Наприклад.
Скільки різних танцюючих пар можна скласти із трьох дівчат та двох юнаків?
Розв’язання.
Для танцюючою пари необхідно вибрати і хлопця, і дівчину. Причому кількість способів вибрати дівчину не залежить від того, якого хлопця вже було обрано. За правилом добутку маємо 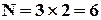 пар.
пар.
Складний вибір об'єктів
Часто у комбінаторних задачах вибір об'єктів здійснюється в кілька етапів, на деяких працює правило суми, на інших – правило добутку. При складному виборі об'єктів важливо забезпечити повний і систематичний перебір усіх можливих випадків, причому жоден із варіантів не повинен бути врахований кілька разів.
Наприклад.
Нехай є три прапори різних кольорів. На флагштоці піднімається сигнал, що складається не менше, ніж із двох прапорів. Скільки різних сигналів можна підняти на флагштоці, якщо порядок прапорів у сигналі враховується?
Розв’язання.
Сигнал можна скласти або із 2-х прапорів, або із 3-х. Позначимо через 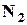 – кількість способів скласти сигнал із 2-х прапорів, а через
– кількість способів скласти сигнал із 2-х прапорів, а через 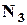 – із 3-х відповідно. Одночасне виконання цих двох дій неможливо. Тоді, загальна кількість способів скласти сигнал за правилом суми дорівнює:
– із 3-х відповідно. Одночасне виконання цих двох дій неможливо. Тоді, загальна кількість способів скласти сигнал за правилом суми дорівнює: 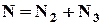 . Розрахуємо
. Розрахуємо 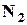 . Кількість способів вибрати перший прапор для сигналу, що складається із 2 прапорів, дорівнює 3. Кількість способів вибрати другий прапор для сигналу, що складається із 2 прапорів, дорівнює 2, бо один з 3 прапорів вже був використаний. Треба підняти і перший, і другий прапори, але кількість способів вибрати другий прапор для сигналу не залежить від того, який конкретно прапор був обраний на першому етапі. Тоді, за правилом добутку знаходимо:
. Кількість способів вибрати перший прапор для сигналу, що складається із 2 прапорів, дорівнює 3. Кількість способів вибрати другий прапор для сигналу, що складається із 2 прапорів, дорівнює 2, бо один з 3 прапорів вже був використаний. Треба підняти і перший, і другий прапори, але кількість способів вибрати другий прапор для сигналу не залежить від того, який конкретно прапор був обраний на першому етапі. Тоді, за правилом добутку знаходимо: 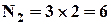 . Аналогічно, отримуємо,
. Аналогічно, отримуємо, 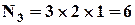 , тоді
, тоді 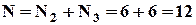 .
.
Тема 1
Основні комбінаторні з'єднання без повторень елементів
З'єднання – прості комбінаторні конфігурації, до яких відносять:
– перестановки,
– сполучення,
– розміщення.
Перестановки
Перестановкою із n елементів або n-перестановкою називають упорядковану послідовність (кортеж, вектор) елементів множини.
Дві перестановки вважаються різними, якщо вони відрізняються порядком розташування елементів в них.
Наприклад.
Нехай є множина 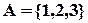 . Згенерувати усі перестановки елементів цієї множини. Перестановки:
. Згенерувати усі перестановки елементів цієї множини. Перестановки: 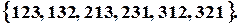 Перестановки згенеровані у порядку зростання натуральних чисел, поставлених у відповідність кожній з них.
Перестановки згенеровані у порядку зростання натуральних чисел, поставлених у відповідність кожній з них.
Теорема 1
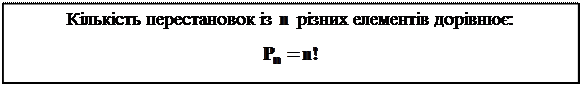
Примітка: визначимо 0! = 1.
Доведення.
Нехай є  різних об'єктів (наприклад. куль з різними номерами) і їх необхідно розташувати на
різних об'єктів (наприклад. куль з різними номерами) і їх необхідно розташувати на  різних місць (комірок з різними номерами). На перше місце (або у першу комірку) можна розмістити будь-який із наявних
різних місць (комірок з різними номерами). На перше місце (або у першу комірку) можна розмістити будь-який із наявних  елементів. Після цього, на друге місце можна розмістити будь-який із
елементів. Після цього, на друге місце можна розмістити будь-який із 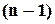 елемента, що лишилися. Зауважимо, що число претендентів на друге місце не залежить від того, який конкретно елемент був обраний на перше місце. Далі на 3 місце –
елемента, що лишилися. Зауважимо, що число претендентів на друге місце не залежить від того, який конкретно елемент був обраний на перше місце. Далі на 3 місце – 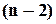 претендента і так далі. На останнє місце залишиться один претендент. За правилом добутку маємо:
претендента і так далі. На останнє місце залишиться один претендент. За правилом добутку маємо: 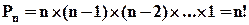 .
.
Наприклад.
1) Скільки різних перестановок можна згенерувати із елементів множини 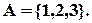
Розв’язання.
Кількість усіх перестановок у множині, що має 3 різні елементи дорівнює: 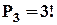 .
.
2) Скільки різних слів можна утворити, переставляючи букви в слові "домбра"?
Розв’язання.
Оскільки усі літери у слові "домбра" різні та нас цікавить тільки порядок розташування цих літер, то 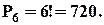
3) Трійка дівчат водять хоровод. Скількома способами вони можуть стати у коло?
Розв’язання.
Якщо дівчата стояли б на місці (кожне місце мало б номер), то вийшло б 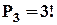 способів стати в коло. Але так, як дівчата водять хоровод, то їх розташування відносно оточення неважливе, а важливо, як вони розташовані одна відносно іншої. Тобто існують перестановки,що переходять одна в іншу. Наприклад, якщо взяти усі перестановки із 3 цифр, то їх можна розбити на 2 групи, причому у кожній із цих груп перестановки не відрізняються:
способів стати в коло. Але так, як дівчата водять хоровод, то їх розташування відносно оточення неважливе, а важливо, як вони розташовані одна відносно іншої. Тобто існують перестановки,що переходять одна в іншу. Наприклад, якщо взяти усі перестановки із 3 цифр, то їх можна розбити на 2 групи, причому у кожній із цих груп перестановки не відрізняються:
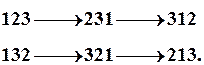
Тоді, кількість різних перестановок дівчат у хороводі дорівнює:
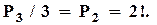
Розміщення
(  - перестановки)
- перестановки)
Розміщення із  по
по  – упорядкована послідовність із
– упорядкована послідовність із  елементів множини, що містить всього
елементів множини, що містить всього  елементів.
елементів.
Два розміщення вважаються різними, якщо вони відрізняються:
– складом елементів;
– порядком розташування елементів;
– і тим, і другим.
Наприклад.
Нехай є множина 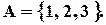
Згенерувати усі розміщення із 3 по 2. Розміщення із 3 по 2 для 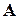 :
: 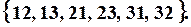
Два розміщення 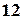 та
та 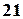 – відрізняються порядком розташування елементів;
– відрізняються порядком розташування елементів; 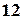 та
та 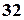 – відрізняються складом елементів; а
– відрізняються складом елементів; а 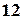 та
та 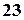 – і складом, і порядком розташування елементів.
– і складом, і порядком розташування елементів.
Теорема 2
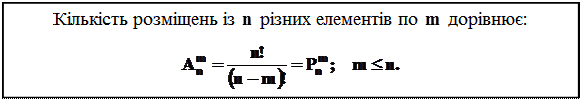
Примітка: при 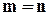 :
:
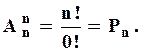
Доведення.
Нехай є  різних об'єктів і їх необхідно розмістити на
різних об'єктів і їх необхідно розмістити на  різних місць. На 1-е місце є
різних місць. На 1-е місце є  претендентів, на 2-е –
претендентів, на 2-е – 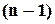 претендент, на третє –
претендент, на третє – 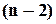 , ..., на
, ..., на  -е місце –
-е місце – 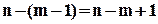 претендентів. За правилом добутку отримаємо, що кількість різних розміщень із
претендентів. За правилом добутку отримаємо, що кількість різних розміщень із  по
по  складає:
складає:
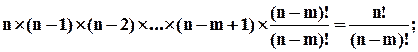
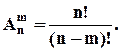
Наприклад.
1) Скількома способами можна розставити на полиці 5 книг із 7?
Розв’язання.
Оскільки усі книжки різні, то нас цікавить і які книжки будуть розставлені на полиці, і у якому порядку:
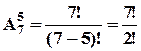 .
.
2) Скільки різних чотирьохлітерних ідентифікаторів можна отримати, використовуючи літери алфавіту 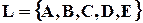 , якщо ні одна із літер не повторюється?
, якщо ні одна із літер не повторюється?
Розв’язання.
У алфавіті 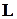 всього 5 літер, 4 із них вони повинні бути використані для генерування ідентифікатору, причому порядок літер у ідентифікаторі має значення:
всього 5 літер, 4 із них вони повинні бути використані для генерування ідентифікатору, причому порядок літер у ідентифікаторі має значення:
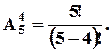
Сполучення
Сполучення із  по
по  – набір з
– набір з  елементів множини, що містить
елементів множини, що містить  різних елементів, без урахування порядку елементів у наборі.
різних елементів, без урахування порядку елементів у наборі.
Різні сполучення відрізняються один від одного тільки складом елементів, але не їх порядком.
Наприклад.
Нехай є множина 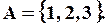
Згенерувати усі сполучення із 3 по 2.
Сполучення із 3 по 2 для 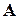 :
: 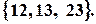
Теорема 3
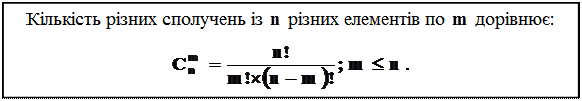
Доведення.
Кожне сполучення із  елементів можна упорядкувати
елементів можна упорядкувати 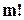 способами, тобто з нього виходить
способами, тобто з нього виходить 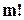 перестановок. Для усіх
перестановок. Для усіх 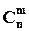 сполучень маємо
сполучень маємо 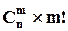 перестановок, але це число дорівнює кількості різних розміщень із
перестановок, але це число дорівнює кількості різних розміщень із  елементів по
елементів по  , а отже,
, а отже, 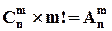 . Тоді, використовуючи теорему 2 маємо:
. Тоді, використовуючи теорему 2 маємо:
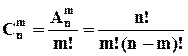 .
.
Властивості числа сполучень
1. 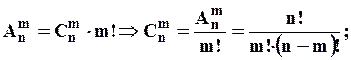
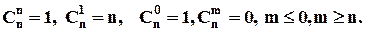
2. Симетричність числа сполучень:
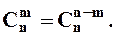
3. Правило Паскаля
Для числа сполучень із  по
по  справедливе наступне рекурентне співвідношення:
справедливе наступне рекурентне співвідношення:
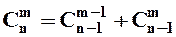 .
.
4. Біном Ньютона:
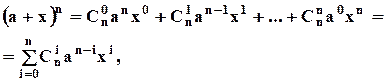
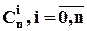 – біноміальні коефіцієнти.
– біноміальні коефіцієнти.
При 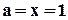 сума біноміальних коефіцієнтів дорівнює:
сума біноміальних коефіцієнтів дорівнює:
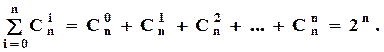
Наприклад.
1) Скількома способами із 25 членів наукового товариства можна обрати президію в кількості 3 осіб?
Розв’язання.
Оскільки треба обрати 3 осіб для роботи у президії наукового товариства, то порядок вибору значення не має, а має значення тільки, які особи із 25 наявних увійдуть у склад президії. Тоді, число способів обрати президію у складі із 3 осіб дорівнює: 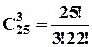 .
.
2) Скількома способами із 25 осіб наукового товариства можна обрати президента, віцепрезидента та вченого секретаря?
Розв’язання.
У даному випадку має значення і склад обраних осіб, і порядок їх обрання, бо вони будуть мати різні повноваження. Перший із обраних буде президентом наукового товариства, другий – віцепрезидентом, а третій секретарем: 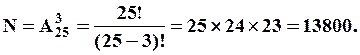
З другого боку, спочатку можна вибрати трьох осіб 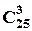 способами, а потім обчислити кількість способів роздати їм повноваження:
способами, а потім обчислити кількість способів роздати їм повноваження: 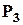 . Оскільки мають значення і які особи обрані, і які повноваження кожен з них отримав, то за правилом добутку маємо
. Оскільки мають значення і які особи обрані, і які повноваження кожен з них отримав, то за правилом добутку маємо 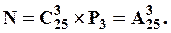
Третій варіант міркувань полягає у застосуванні тільки правила добутку. Президент наукового товариства може бути обраний 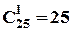 способами. Після цього і незалежно від цього, віцепрезидент може бути обраний вже
способами. Після цього і незалежно від цього, віцепрезидент може бути обраний вже 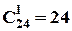 способами. Відповідно, секретар,
способами. Відповідно, секретар, 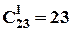 способами. За правилом добутку маємо:
способами. За правилом добутку маємо: 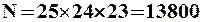 .
.
2. На книжковій полиці розміщується 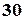 томів книг. Скількома способами можна розставити їх так, щоб
томів книг. Скількома способами можна розставити їх так, щоб 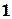 та
та 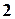 томи не стояли поряд?
томи не стояли поряд?
Розв’язання.
Задача легше розв’язується через зворотну задачу. 30 томів книг можна розставити на полиці без будь-яких обмежень 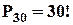 способами. Обчислимо число способів розставити книжки так, що
способами. Обчислимо число способів розставити книжки так, що 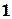 й
й 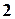 том будуть стояти поряд. Перший та другий том можна поставити поряд
том будуть стояти поряд. Перший та другий том можна поставити поряд 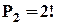 способами (
способами ( 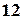 або
або 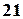 ). Далі маємо розставити на полиці
). Далі маємо розставити на полиці 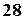 окремих томів та один складний об'єкт, що складається із
окремих томів та один складний об'єкт, що складається із 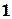 та
та 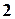 томів:
томів: 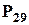 .
.
За правилом добутку маємо рішення зворотної задачі: 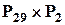 .
.
Тоді, пряма задача має наступний розв’язок:
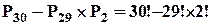 .
.
3. Чотири стрілка повинні вразити 8 мішеней (кожен по 2). Скількома способами вони можуть розподілити мішені між собою?
Розв’язання.
Для кожного стрілка має значення, які мішені йому будуть розподілені, але не має значення у якому порядку він буде в них стріляти. Тому, число варіантів вибору двох мішеней із 8 для першого стрілка дорівнює 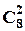 , для другого –
, для другого – 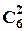 , для третього відповідно –
, для третього відповідно – 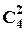 , для останнього –
, для останнього – 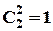 . За правилом добутку:
. За правилом добутку: 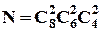 .
.
4. Колода у 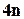 карт містить 4 масті по
карт містить 4 масті по  карт у кожній.
карт у кожній.
Скількома способами можна вибрати:
1) 5 карт, 4 з яких з однаковими номерами?
2) три карти з одними номерами та 2 з іншими однаковими номерами?
Розв’язання.
1) Для того, щоб вибрати 4 карти із одним номером достатньо із наявних  номерів вибрати один, а останню, 5 карту вибрати із колоди без 4 карт із цим номером:
номерів вибрати один, а останню, 5 карту вибрати із колоди без 4 карт із цим номером: 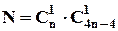 .
.
2) Для того, щоб вибрати 3 карти із одним номером треба спочатку вибрати один номер із  існуючих, а потім із 4 карт з таким номером вибрати три карти:
існуючих, а потім із 4 карт з таким номером вибрати три карти: 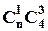 . Аналогічно вибираємо дві карти з однаковими номерами:
. Аналогічно вибираємо дві карти з однаковими номерами: 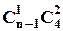 , але номер вибираємо із
, але номер вибираємо із 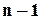 варіанту.
варіанту.
Тоді, 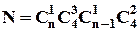 за правилом добутку.
за правилом добутку.
5. Хор складається з 10 учасників. Скількома способами можна протягом 3-х днів вибирати по 6 учасників так, щоб кожен день були різні склади хору?
Розв’язання.
Порядок виступів важливий (який склад хору, в який день виступає),
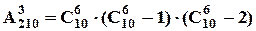 ,
,
не важливий:
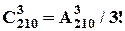 .
.
5) Скількома способами можна переставити літери слова "паралелізм", щоб не змінювався порядок голосних?
Розв’язання.
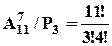
Тема 2




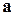 може бути вибраний
може бути вибраний  способами, а об'єкт
способами, а об'єкт 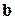 –
–  іншими способами, то вибір "
іншими способами, то вибір " 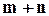 способами.
способами.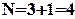 .
.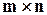 способами.
способами.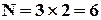 пар.
пар.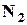 – кількість способів скласти сигнал із 2-х прапорів, а через
– кількість способів скласти сигнал із 2-х прапорів, а через 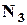 – із 3-х відповідно. Одночасне виконання цих двох дій неможливо. Тоді, загальна кількість способів скласти сигнал за правилом суми дорівнює:
– із 3-х відповідно. Одночасне виконання цих двох дій неможливо. Тоді, загальна кількість способів скласти сигнал за правилом суми дорівнює: 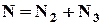 . Розрахуємо
. Розрахуємо 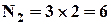 . Аналогічно, отримуємо,
. Аналогічно, отримуємо, 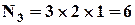 , тоді
, тоді 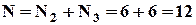 .
.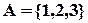 . Згенерувати усі перестановки елементів цієї множини. Перестановки:
. Згенерувати усі перестановки елементів цієї множини. Перестановки: 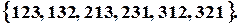 Перестановки згенеровані у порядку зростання натуральних чисел, поставлених у відповідність кожній з них.
Перестановки згенеровані у порядку зростання натуральних чисел, поставлених у відповідність кожній з них.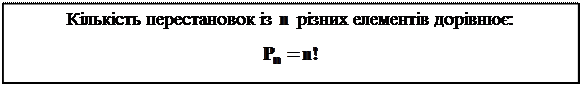
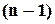 елемента, що лишилися. Зауважимо, що число претендентів на друге місце не залежить від того, який конкретно елемент був обраний на перше місце. Далі на 3 місце –
елемента, що лишилися. Зауважимо, що число претендентів на друге місце не залежить від того, який конкретно елемент був обраний на перше місце. Далі на 3 місце – 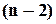 претендента і так далі. На останнє місце залишиться один претендент. За правилом добутку маємо:
претендента і так далі. На останнє місце залишиться один претендент. За правилом добутку маємо: 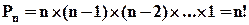 .
.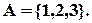
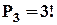 .
.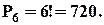
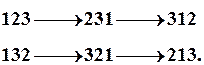
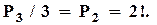
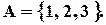
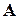 :
: 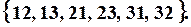
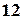 та
та 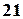 – відрізняються порядком розташування елементів;
– відрізняються порядком розташування елементів; 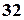 – відрізняються складом елементів; а
– відрізняються складом елементів; а  – і складом, і порядком розташування елементів.
– і складом, і порядком розташування елементів.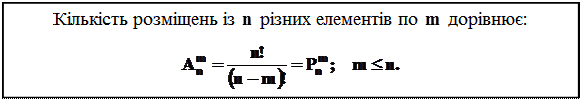
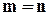 :
: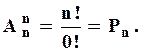
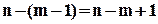 претендентів. За правилом добутку отримаємо, що кількість різних розміщень із
претендентів. За правилом добутку отримаємо, що кількість різних розміщень із 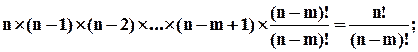
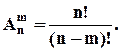
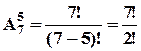 .
.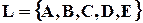 , якщо ні одна із літер не повторюється?
, якщо ні одна із літер не повторюється?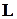 всього 5 літер, 4 із них вони повинні бути використані для генерування ідентифікатору, причому порядок літер у ідентифікаторі має значення:
всього 5 літер, 4 із них вони повинні бути використані для генерування ідентифікатору, причому порядок літер у ідентифікаторі має значення: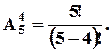
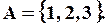
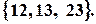
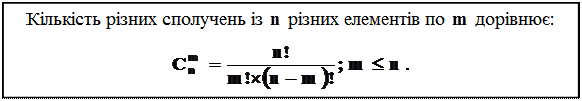
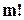 способами, тобто з нього виходить
способами, тобто з нього виходить 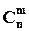 сполучень маємо
сполучень маємо 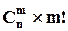 перестановок, але це число дорівнює кількості різних розміщень із
перестановок, але це число дорівнює кількості різних розміщень із 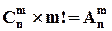 . Тоді, використовуючи теорему 2 маємо:
. Тоді, використовуючи теорему 2 маємо: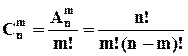 .
.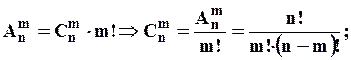
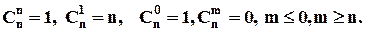
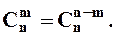
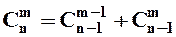 .
.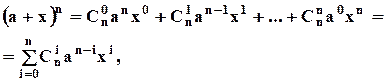
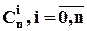 – біноміальні коефіцієнти.
– біноміальні коефіцієнти.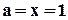 сума біноміальних коефіцієнтів дорівнює:
сума біноміальних коефіцієнтів дорівнює: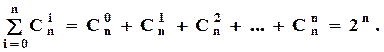
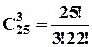 .
.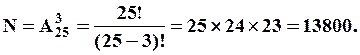
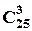 способами, а потім обчислити кількість способів роздати їм повноваження:
способами, а потім обчислити кількість способів роздати їм повноваження: 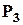 . Оскільки мають значення і які особи обрані, і які повноваження кожен з них отримав, то за правилом добутку маємо
. Оскільки мають значення і які особи обрані, і які повноваження кожен з них отримав, то за правилом добутку маємо 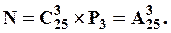
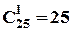 способами. Після цього і незалежно від цього, віцепрезидент може бути обраний вже
способами. Після цього і незалежно від цього, віцепрезидент може бути обраний вже 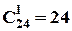 способами. Відповідно, секретар,
способами. Відповідно, секретар, 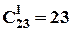 способами. За правилом добутку маємо:
способами. За правилом добутку маємо: 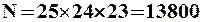 .
.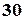 томів книг. Скількома способами можна розставити їх так, щоб
томів книг. Скількома способами можна розставити їх так, щоб 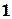 та
та 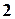 томи не стояли поряд?
томи не стояли поряд?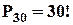 способами. Обчислимо число способів розставити книжки так, що
способами. Обчислимо число способів розставити книжки так, що 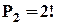 способами (
способами ( 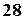 окремих томів та один складний об'єкт, що складається із
окремих томів та один складний об'єкт, що складається із 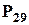 .
.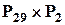 .
.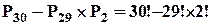 .
.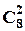 , для другого –
, для другого – 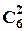 , для третього відповідно –
, для третього відповідно – 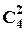 , для останнього –
, для останнього – 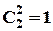 . За правилом добутку:
. За правилом добутку: 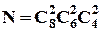 .
.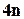 карт містить 4 масті по
карт містить 4 масті по 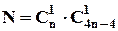 .
.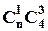 . Аналогічно вибираємо дві карти з однаковими номерами:
. Аналогічно вибираємо дві карти з однаковими номерами: 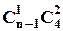 , але номер вибираємо із
, але номер вибираємо із 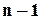 варіанту.
варіанту.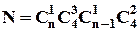 за правилом добутку.
за правилом добутку.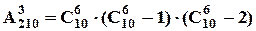 ,
,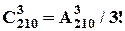 .
.