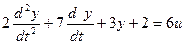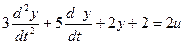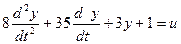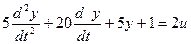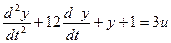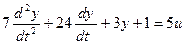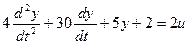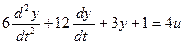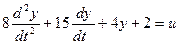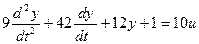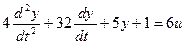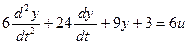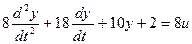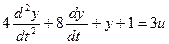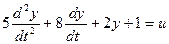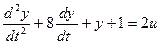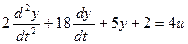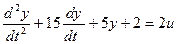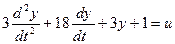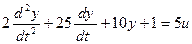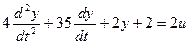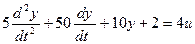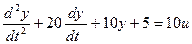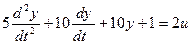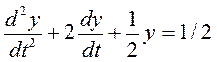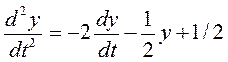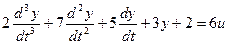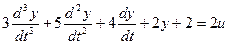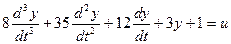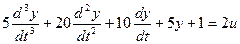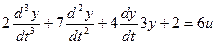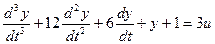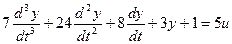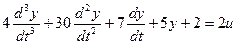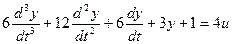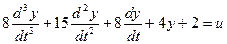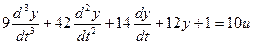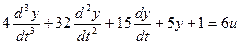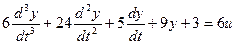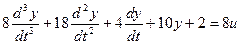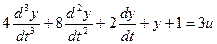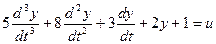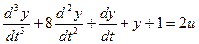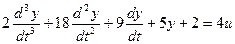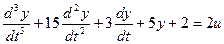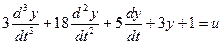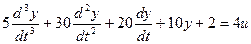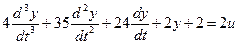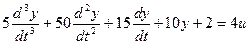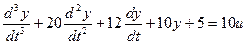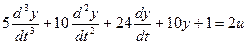ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РФ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕКСТИЛЬНЫЙ УНИВЕРСИТЕТ
им. А.Н.КОСЫГИНА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к лабораторному практикуму по курсу
«Математическое моделирование объектов и систем управления
в программе Matlab»
Авторы: Тимохин А.Н.
Румянцев Ю.Д.
Москва 2012 г.
ЛАБОРАТОРНАЯ РАБОТА №1
Численное решение нелинейных уравнений
Цель работы: Изучить принципы численного решения нелинейных уравнений построения линейных моделей в программе MATLAB и получения переходных процессов с заданными характеристиками.
Задание:
а). по заданному преподавателем варианту (см. таблицу 1.1) построить график уравнения.
б) найти корни уравнения, пользуясь различными способами программы MATLAB.
в).провести исследование предложенной функции на предмет изменения числа корней при изменении пределов заданного отрезка.
Основные положения
Ниже перечислены встроенные в MATLAB тригонометрические функции и обратные к ним:
sin, cos, tan, cot —синус, косинус, тангенс и котангенс;
sec, csc —секанс, косеканс
asin, acos, atan, acot — арксинус, арккосинус, арктангенс и арккотангенс;
asec, acsc — арксеканс, арккосеканс..
Аргументы тригонометрических функций должны быть выражены в радианах. Обратные тригонометрические функции возвращают результат также в радианах.
В MATLAB встроены следующие гиперболические функции и обратные к ним:
sinh, cosh, tanh, coth — гиперболические синус, косинус, тангенс и котангенс;
sech, csch — гиперболические секанс и косеканс;
asinh, acosh, atanh, acoth гиперболические арксинус, арккосинус, арктангенс и арккотангенс;
asech, acsch — гиперболические арксеканс и арккосеканс.
Экспоненциальная функция, логарифмы, степенные функции
Ниже перечислены названия этих функций в MATLAB:
eхр — экспоненциальная функция;
loq — натуральный логарифм;
log10 — десятичный логарифм;
log2 — логарифм по основанию 2;
pow2 — возведение числа 2 в степень;
sqrt — квадратный корень;
nextpow2 — степень, в которую надо возвести число 2, чтобы получить ближайшее число (большее или равное аргументу), например
» nextpow2(1000)
ans = 10
Функции для работы с комплексными числами
К ним относятся следующие функции MATLAB:
abs, angle— модуль r и фаза φ (в радианах от -π до π) комплексного числа а + i • b = r • (cos φ + i • sin φ );
complex — конструирует комплексное число по его действительной и мнимой части:
» complex (2.3, 5.8)
ans =
2.3000 + 5.8000i
conj — возвращает комплексно-сопряженное число;
imag, real — мнимая и действительная часть комплексного числа.
Округление и остаток от деления
Ниже приведены примеры использования этих функций в MATLAB:
fix — округление до ближайшего целого по направлению к нулю:
» fix(1.8) » fix{-1.9)
ans = ans -
1 -1
floor, ceil — округление до ближайшего целого по направлению к минус бесконечности или плюс бесконечности:
» floor(3.2) » ceil(3.2)
ans = ans =
3 4
round —округление до ближайшего целого:
» round(4.1) » round{4.5)
ans = ans =
4 5
mod—остаток от целочисленного деления (со знаком второго аргумента):
» mod(5,2) » mod(5,-2)
ans = ans -
1 -1
rem — остаток от целочисленного деления (со знаком первого аргумента):
» rem(5,2) » rem(5,-2)
ans =• ans =
1 1
sign — знак числа.
Численное решение нелинейных уравнений
Задача нахождения корней нелинейных уравнений встречается в различ-ных областях научно-технических исследований. Проблема формулируется следующим образом: Пусть задана непрерывная функция f(x) и требуется найти корень уравнения
f(х0) = 0.
Будем предполагать, что имеется интервал изменения х [а; b], на котором необходимо исследовать функцию f(x) и найти значение x0, при котором f(x0) равно или весьма мало отличается от нуля.
Вначале необходимо построить график функции f(x) на заданном интервале и убедиться в существовании корня или нескольких корней. Затем применить программы поиска корней. Если существует один корень и график f(x) пересекает ось ох, то можно применить оператор fzero.
Если f(x) имеет больше одного корня и может касаться и пересекать ось ох, то следует применить более мощную программу fsolve из пакета Optimization Toolbox, которая решает задачу методом наименьших квадратов. Программа fzero использует известные численные методы: деление отрезка пополам, секущей и обратной квадратичной интерполяции.
Корни многочленов определяются оператором roots. Один из способов применения этого оператора показан на примере 1.
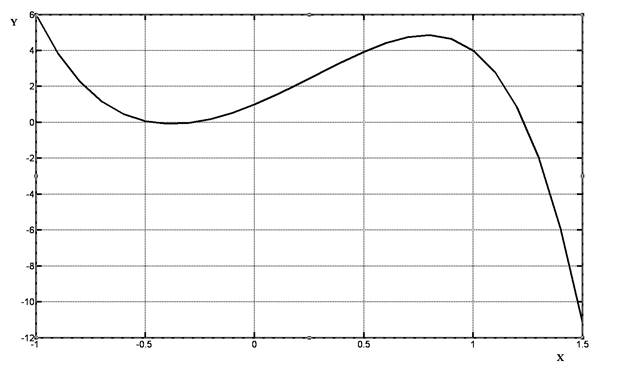
Имеется функция y=-2x5-4x3+4x2+5x+1 на отрезке ( -1, 1.5).
Определим эту функцию в MATLAB:
>> x=-1:.1:1.5;
>> y=-2*x.^5-4*x.^3+4*x.^2+5*x+1;
Определим коэффициенты:
>> coef=[-2 0 -4 4 5 1]
coef =
-2 0 -4 4 5 1
Определим корни:
>> roots(coef)
ans =
-0.2397 + 1.7238i
-0.2397 - 1.7238i
1.2348
-0.4727
-0.2828
Построим график:
>> plot(x,y,'k'),grid on
>>
График функции показан на рисунке 1.1.
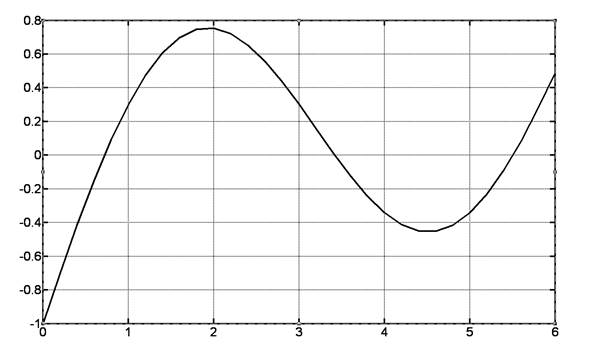
Пример 2. Найти корень нелинейного уравнения (sin(x)-cos(sqrt(x))=0 на интервале [0.0; 6.0].
Протокол программы
» % Строим график заданной функции
» x = 0.0 : 0.1: 6.0; у = (sin(x)-cos(sqrt(x));
» plot (x, у); grid on
Появляется окно с графиком функции (sin(x)-cos(sqrt(x)) , (Рис. 1.2) из которого следует, что корни функции на заданном интервале существует. Для точного определения корня применяем fzero и fsolve.
» X1 =fzero (' ((sin(x)-cos(sqrt(x)) ', [0.0 6.0])
Результат решения
X 1 =
5.5072
Как видим, найден только один последний корень. Применим более мощную программу fsolve.
» Х2 = fsolve (' ((sin(x)-cos(sqrt(x))', 0.0 : 6.0)
Результат решения
X2=
0.7214 0.7214 3.4202 3.4202 3.4202 5.5072 5.5072
В этом случае найдены все три корня уравнения.
Порядок выполнения работы
1. По заданному варианту уравнений из таблиц 1.1 и 1.2 построить графики на предложенных интервалах.
2. Найти имеющиеся корни уравнений, применяя операторы roots, fzero и fsolve.
3. Исследовать предложенные уравнения на наличие корней, увеличивая заданный интервал слева и справа.
4. Скопировать результаты работы в файл формата *.doc для предъявления отчета и защиты работы.
Варианты заданий .
Таблица 1.1
| № п/п
| Функция
| Границы отрезка
|
| 1
| y=-2x5-4x3+4x2+5x+1
| [-1; 2]
|
| 2
| y=x5-4x3+4x2+5x+1
| [-2; 2]
|
| 3
| y=x 6 -x5-4x3+4x2+5x+1
| [-2; 1.5]
|
| 4
| y=x 6 -x5-4x3+2x2+5x+5
| [-2; 2]
|
| 5
| y=x 6 -x5-4x3+4x2+5x+3
| [-1; 1.3]
|
| 6
| y=-x 6 -x5-4x3+3x2+5x+4
| [-1; 2.5]
|
| 7
| y=-x 6 -4x5-4x3+4x2+5x+2
| [-1; 1.5]
|
| 8
| y=x 6 -3x5-x3+3x2+5x+6
| [-1.5; 2.5]
|
| 9
| y=x 6 -x5-3x3+2x2+5x+4
| [-1.2; 1.6]
|
| 10
| y=-x 6 -x5-4x3+4x2+5x+7
| [-1.3; 1.7]
|
| 11
| y=-x 6 -x5-2x3+3x2+5x+3
| [-1.2; 2.5]
|
| 12
| y=x 6 -x5-3x3+2x+4
| [-1.3; 2.5]
|
| 13
| y=x 6 -x5-4x3+4x2+5x+8
| [-1.2; 1.5]
|
| 14
| y=x 6 -4x3+2x2+3x+2
| [-1.4; 1.6]
|
| 15
| y=x 6 -x5-4x3+4x2+5x+4
| [-1; 2.5]
|
| 16
| y=-x 6 -3x5-4x3+4x2+5x+3
| [-1.3; 1.6]
|
| 17
| y=2x 6 -4x3+4x2+5x+5
| [-1.2; 1.7]
|
| 18
| y=x 6 –x5-4x3+4x2+5x+7
| [-1.1; 1.5]
|
| 19
| y=x 6 -2x5-5x3+4x2+5x+5
| [-1.5; 1.5]
|
| 20
| y=x 6 -4x5-3x3+4x2+5x+4
| [-1.2; 2.5]
|
| 21
| y=x 6 -5x5-4x3+4x2+5x+6
| [-1.3; 1.5]
|
| 22
| y=-x 6 -x5-4x3+4x2+5x+2
| [-1.5; 1.7]
|
| 23
| y=-5x 6 -x5-4x3+4x2+5x+4
| [-1.7; 2.5]
|
| 24
| y=-3x 6 -x5-4x3+4x2+5x+2
| [-1.2; 1.5]
|
| 25
| y=-2x 6 -x5-4x3+4x2+5x+3
| [-1.5; 2.5]
|
| 26
| y=-4x 6 -x5-4x3+4x2+5x+7
| [-1; 1.5]
|
Таблица 1.2
| 1
| 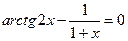
| [0.0; 1.0]
|
| 2
| ех-ln х-20 = 0
| [3.0; 3.21
|
| 3
| 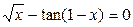
| [0.0; 1.0]
|
| 4
| 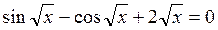
| [0.0; 0.2]
|
| 5
| x4 +2x3 –x -1=0
| [0.8; 1.0]
|
| 6
| x3 –e4x -5.5=0
| [2.6; 3.0]
|
| 7
| x6 -3x2 +x-1 = 0
| [1.0; 1.5]
|
| 8
| 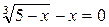
| [1.0; 2.0]
|
| 9
| x2 –ln x = 0
| [0.0; 1.0]
|
| 10
| x2 –cos x = 0
| [0.0; 1.0]
|
| 11
| ln x – arctg x = 0
| [3.0; 4.01
|
| 12
| x2 arctg x -1 = 0
| [1.0; 1.2]
|
| 13
| x2 +ln x – 4 = 0
| [1.0; 2.01
|
| 14
| x – arctg x = 0
| [0.0; 1.0]
|
| 15
| x2 – ex – 2 = 0
| [-0.2; -0.11]
|
| 16
| x2 – ln(x+1) = 0
| [0.1; 0.9]
|
| 17
| x5 – x -2 =0
| [1.0; 1.4]
|
| 18
| 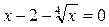
| [3.0; 4.0]
|
| 19
| x - tg x =0
| [0.0; 1.51
|
| 20
| x + ln x – 0.5 = 0
| [0.0; 1.0]
|
| 21
| 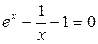
| [0.1; 1.0]
|
| 22
| arctg(x)-1 = 0
| [0.4; 0.6]
|
| 23
| 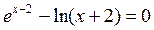
| [3.0; 4.0]
|
| 24
| х3-9х2+5х-6 = 0
| [4.0; 5.0]
|
| 25
| arcos 2x – x2 -0.35 =0
| [2.0; 3.0]
|
| 26
| x2 –ln(1+x2) -9.7 = 0
| [0.0; 0.48]
|
Содержание отчета:
1. График функции с четкой оцифровкой осей координат.
2. Значения найденных корней на интервале варианта.
3. График функции с изменённым интервалом.
4. Значения найденных корней на изменённом интервале.
Лабораторная работа №2.
Решение дифференциальных уравнений.
Цель работы: Изучить принципы численного решения нелинейных уравнений построения линейных моделей в программе MATLAB и получения переходных процессов с заданными характеристиками.
Задание:
а). по заданному преподавателем варианту (см. таблицу 1.1) построить график уравнения.
б) найти корни уравнения, пользуясь различными способами программы MATLAB.
в).провести исследование предложенной функции на предмет изменения числа корней при изменении пределов заданного отрезка.
Основные положения
Для решения обычных дифференциальных уравнений можно применить функцию dsolve. Это символьное решение уравнений.
По умолчанию независимая переменная - 't'. Символ 'D' обозначает дифференцирование относительно независимой переменной.
Символ 'D' сопровождается цифрой.
Первая производная d/dt обозначается "D".
Вторая производная d^2/dt^2 обозначается"D2" и т.д.
Например, D3y обозначает третью производную от y (t). Заметим, что имена символьных переменных не должны содержать 'D'.
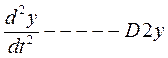
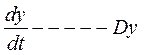
Решим следующее уравнение:
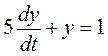
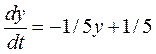 Выделим старшую производную:
Выделим старшую производную:
Применим функцию dsolve в командной строке Matlab, написав полученное уравнение в одинарных кавычках, а через запятую в кавычках укажем начальное значение переменной и имя аргумента. Для уравнения второго порядка нужно указать через запятую начальные значения переменной и её производной. Для уравнения третьего порядка указываются три начальных условия и т.д.
>> dsolve('Dy=-1/5*y+1/5','y(0)=0','t')
ans =
1-exp(-1/5*t)
>>
Полученную формулу можно использовать для построения графика функции.
Программа
clear
y(1)=0;
t=2:20;
y(t)=1-exp(-1/5*t);
plot (y),grid on

Поскольку в вышеприведенной программе индекс переменной (t) и аргумент функции совпадают, то шаг вычисления равен индексу, а это только целое число. График функции в большинстве случаев получается с изломами.
Чтобы уменьшить шаг вычисления, изменять его удобнее в цикле.
Обозначим индекс t1, а аргумент вычисления t.
Аргумент изменяется с шагом 0.1.
clear
y(1)=0;
t=0;
for t1=2:200;
y(t1)=1-exp(-1/5*t);
t=t+.1;
end
plot (y), grid on
После выполнения программы тот же график получается более гладким.
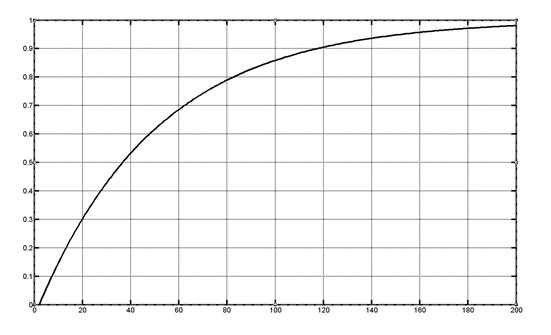
Шаг вычисления в этом случае можно изменять внутри цикла в зависимости от вида функции.
Таблица 2.1
| № вар.
|
Уравнение
| Начальные условия
[ Ý(0) ; Y(0) ]
|
| 1
| 2
| 3
|
| 1
| 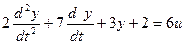
|
[ 1 ; 0 ]
|
| 2
| 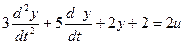
| [ 1 ; 1 ]
|
| 3
| 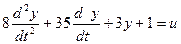
| [ 0 ; 1 ]
|
| 4
| 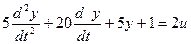
| [ 0.2 ; 0.5 ]
|
| 5
| 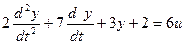
| [ 0.4 ; 0.8 ]
|
| 6
| 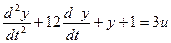
| [ 0.5 ; 0 ]
|
| 7
| 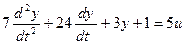
| [ 0 ; 0.5 ]
|
| 8
| 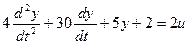
| [ 0.2 ; 0.5 ]
|
| 9
| 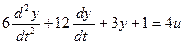
| [ 0 ; 1 ]
|
| 10
| 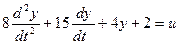
| [ 0.2 ; 0 ]
|
| 11
| 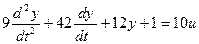
| [ 0 ; 2 ]
|
| 12
| 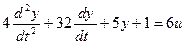
| [ 0.25 ; 1 ]
|
| 13
| 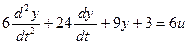
| [ 0.5 ; 0.5 ]
|
| 1
| 2
| 3
|
| 14
| 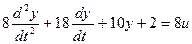
| [ 0 ; 1 ]
|
| 15
| 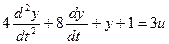
| [ 0.2 ; 0.5 ]
|
| 16
| 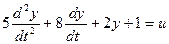
| [ 0.3 ; 0 ]
|
| 17
| 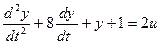
| [ 0 ; 0.5 ]
|
| 18
| 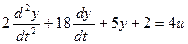
| [ 0.24 ; 1 ]
|
| 19
| 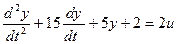
| [ 0.2 ; 0 ]
|
| 20
| 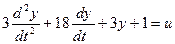
| [ 0.1 ; 0.25 ]
|
| 21
| 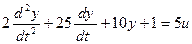
| [ 0.3 ; 2 ]
|
| 22
| 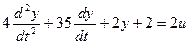
| [ 0 ; 0.25 ]
|
| 23
| 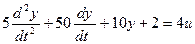
| [ 0.2 ; 0.3 ]
|
| 24
| 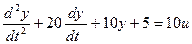
| [ 0 ; 0.5 ]
|
| 25
| 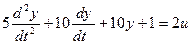
| [ 0.2 ; 0.3 ]
|
Порядок выполнения работы
1. По заданному варианту уравнений из таблицы 2.1 построить график с предложенными начальными условиями.
2. Выбрать шаг вычисления функции с цель получения гладкой кривой графика функции.
3. Выбрать необходимое количество точек вычисления для получения установившегося значения.
4. Установить нулевые начальные условия и получить график этой же функции.
5. Скопировать результаты работы в файл формата *.doc для предъявления отчета и защиты работы.
Содержание отчета:
1. Уравнение варианта.
2. Решение уравнения.
3. Программа построения графика.
4. График функции с четкой оцифровкой осей координат.
5. График функции с изменёнными начальными условиями.
ЛАБОРАТОРНАЯ РАБОТА №3
Решение дифференциальных уравнений программе Simulink .
Цель работы: Изучить принципы численного решения дифференциальных уравнений в программе Simulink и получения переходных процессов с заданными характеристиками.
Задание:
а) По заданному преподавателем варианту (см. таблицу 3.1) построить блок-схему решения уравнения при U=1.
б) Получить график уравнения в стандартном варианте Simulink на приёмнике сигналов Scope.
в) Отредактировать полученный график, установив следующие характеристики: Background – white, Axes line width – 3.0, Axes Color – Black, Font size – 14.0, Line style – Solid line (-), No marker (none), Line width – 3.0, Line Color – Black, (Фон – белый, Толщина линей осей – 3.0, Цвет осей – черный, Шрифт - 14.0, Стиль линии графика – сплошной, без маркеров, Толщина линии графика – 3.0, Цвет линии графика – черный.
Основные положения
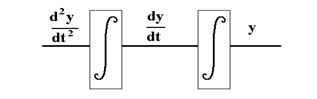
Дифференциальные уравнения решаются путем последовательного интегрирования. Первая производная интегрируется один раз, вторая - два и так далее, как показано на рисунке 3.1.
Решим следующее уравнение:
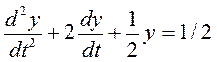
Выделим старшую производную:
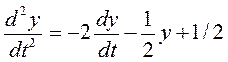
В соответствии с полученным уравнением составим схему набора, показанную на рисунке 3.2.
Начальные условия интегратора установим -2.
Начальные условия интегратора 1 установим 0.
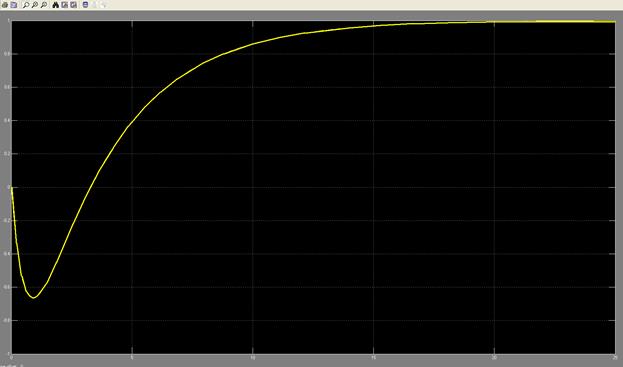
После выполнения получим график. Он показан на рисунке 3.3.
Линия графика на темном фоне не всегда удобна для печати или для вставки такого рисунка в файл формата Word(*.doc). Плохо различимы оказываются сетка и оцифровка осей. Чтобы изменить формат графика, после получения его в стандартном формате, необходимо ввести в строке команд следующий текст:
>>set(0,'ShowHiddenHandles','On')
>>set(gcf,'menubar','figure')
После выполнения этих команд ( Нажать <Enter>) в окне Scope, сверху строки кнопок команд, появится дополнительная строка команд, необходимая для форматирования графика.
После нажатия левой кнопкой мышки (ЛКМ) на Edit, всплывающее подменю позволяет изменять вид графика по усмотрению, пользуясь его командами: Figure Properties, Axes Properties и Current Object Properties.
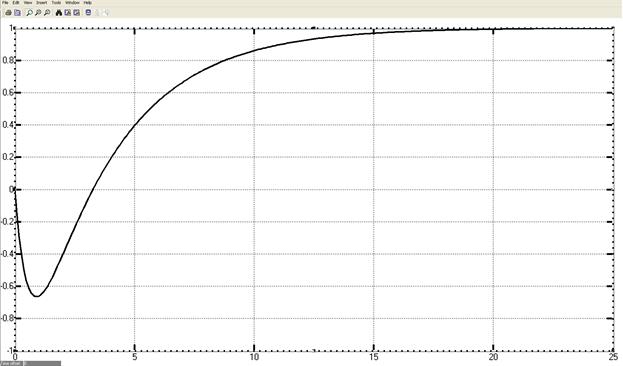
С помощью этих команд можно изменять фон, толщину линей осей, цвет, шрифт, стиль линии графика, толщину линии графика, цвет линии графика. Изменённый формат графика показан на рисунке 3.4.
Таблица 3.1
| № вар.
|
Уравнение
| Начальные условия
[ Ý(0) ; Y(0) ]
|
| 1
| 2
| 3
|
| 1
| 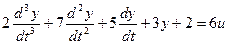
|
[ 1 ; 0 ]
|
| 2
| 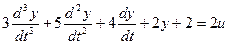
| [ 1 ; 1 ]
|
| 3
| 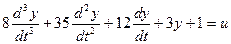
| [ 0 ; 1 ]
|
| 4
| 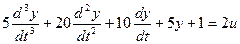
| [ 0.2 ; 0.5 ]
|
| 5
| 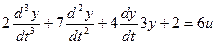
| [ 0.4 ; 0.8 ]
|
| 6
| 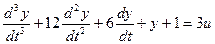
| [ 0.5 ; 0 ]
|
| 7
| 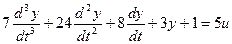
| [ 0 ; 0.5 ]
|
| 8
| 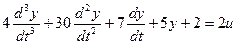
| [ 0.2 ; 0.5 ]
|
| 9
| 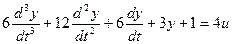
| [ 0 ; 1 ]
|
| 10
| 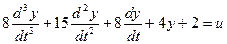
| [ 0.2 ; 0 ]
|
| 11
| 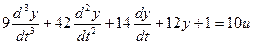
| [ 0 ; 2 ]
|
| 1
| 2
| 3
|
| 12
| 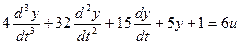
| [ 0.25 ; 1 ]
|
| 13
| 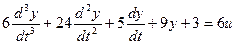
| [ 0.5 ; 0.5 ]
|
| 14
| 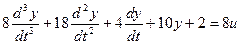
| [ 0 ; 1 ]
|
| 15
| 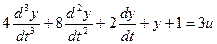
| [ 0.2 ; 0.5 ]
|
| 16
| 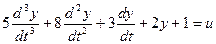
| [ 0.3 ; 0 ]
|
| 17
| 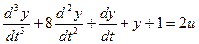
| [ 0 ; 0.5 ]
|
| 18
| 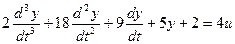
| [ 0.24 ; 1 ]
|
| 19
| 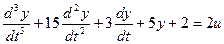
| [ 0.2 ; 0 ]
|
| 20
| 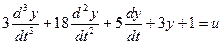
| [ 0.1 ; 0.25 ]
|
| 21
| 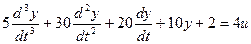
| [ 0.3 ; 2 ]
|
| 22
| 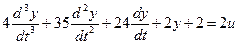
| [ 0 ; 0.25 ]
|
| 23
| 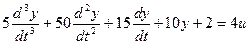
| [ 0.2 ; 0.3 ]
|
| 24
| 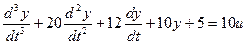
| [ 0 ; 0.5 ]
|
| 25
| 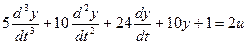
| [ 0.2 ; 0.3 ]
|
Порядок выполнения работы
1. По заданному преподавателем варианту (см. таблицу 3.1) построить блок-схему решения уравнения.
2. Получить график уравнения в стандартном варианте Simulink.
3. Отредактировать полученный график в соответствии с заданием.
4. Скопировать результаты работы в файл формата *.doc для предъявления отчета и защиты работы.
Содержание отчета:
1. Блок-схема решения уравнения по варианту в программе Simulink.
2. Графики решения дифференциальных уравнений с четкой оцифровкой осей координат при различных начальных условиях.
3. Выводы по работе.
ЛАБОРАТОРНАЯ РАБОТА №4



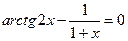
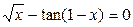
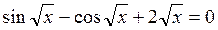
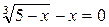
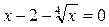
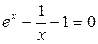
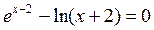
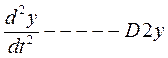
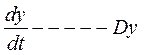
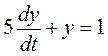
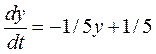 Выделим старшую производную:
Выделим старшую производную: