Цель:
- сформировать навыки вычисления определённых интегралов по формуле Ньютона-Лейбница;
- развить умение интегрировать методом замены переменной;
- закрепить знания о свойствах определённых интегралов;
Материально – техническое обеспечение: методические указания по выполнению работы, стенды «Таблица интегралов»;
Время выполнения: 2 академических часа;
Ход занятия:
1. Изучить краткие теоретические сведения;
2. Выполнить задания;
3. Сделать вывод по работе;
4. Подготовить защиту работы по контрольным вопросам.
Краткие теоретические сведения:
Интеграл, имеющий заданные пределы интегрирования, называют определённым. Непосредственное вычисление определенного интеграла производится по формуле Ньютона – Лейбница:
 где а - нижний предел, b - верхний предел, F ( x )- первообразная функции f ( x ), F ( b )и F ( a )-значения первообразной на концах промежутка.
где а - нижний предел, b - верхний предел, F ( x )- первообразная функции f ( x ), F ( b )и F ( a )-значения первообразной на концах промежутка.
Из этой формулы виден порядок вычисления определенного интеграла:
1) найти одну из первообразных F ( x ) данной функции;
2) вычислить значения F ( x ) при х=а и х= b ;
3) найти разность 
Пример 1. Вычислить интеграл: 
Решение. Используя формулы табличных интегралов 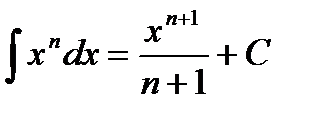 ,
, 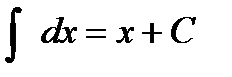 и их свойства получим:
и их свойства получим:

Пример 2. Вычислить интеграл  .
.
Решение. Воспользуемся свойствами степени с дробным отрицательным показателем  и вычислим определенный интеграл по формуле
и вычислим определенный интеграл по формуле  :
: 
Основные свойства определенного интеграла
1. При перестановке пределов интегрирования знак интеграла меняется на противоположный:
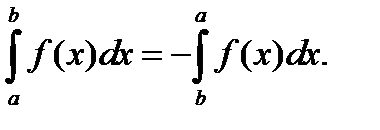
2. Отрезок интегрирования можно разбивать на части:

3. Постоянный множитель можно выносить за знак интеграла:
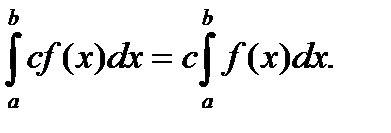
4. Интеграл от суммы функций равен сумме интегралов от всех слагаемых:
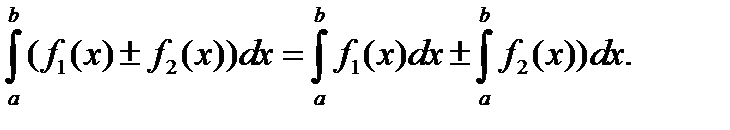
Пример 3. Вычислить интеграл 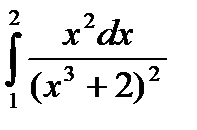 .
.
Решение.
1). Подынтегральная функция является сложной степенной, непосредственное вычисление по формуле Ньютона-Лейбница невозможно, применим интегрирование методом замены переменной. Произведем подстановку 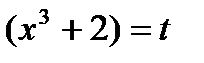 , тогда
, тогда  .
.
2). Определим пределы интегрирования для переменной  . При
. При 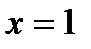 , получаем
, получаем  , при
, при  , находим
, находим 
3) Выразим подынтегральное выражение через  и dt и перейдём к новым пределам интегрирования, в результате получим:
и dt и перейдём к новым пределам интегрирования, в результате получим:

Пример 4. Вычислить интеграл  .
.
Решение. 1). Положим 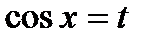 , тогда
, тогда 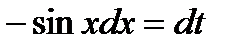 и
и 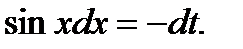
2). Определим новые пределы интегрирования:
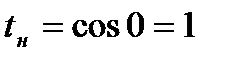 ,
, 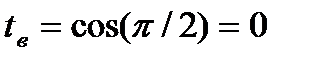 .
.
3). Выразим подынтегральное выражение через t и dt и, применяя свойства определённого интеграла, получим:

Пример 5. Вычислить интеграл  .
.
Решение. Сначала преобразуем подынтегральное выражение 
Затем вычислим интеграл от разности функций, заменив его разностью определенных интегралов от каждой функции:
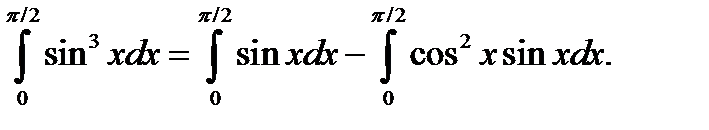
Вычислим каждый интеграл отдельно:


Пусть с os x = t, тогда - sinx dx = dt, откуда sinxdx = - dt, 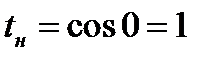 ,
, 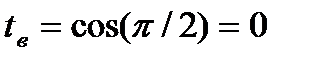 .
.
Тогда, 
Задания для самостоятельного выполнения:
1. Вычислить интеграл по формуле Ньютона - Лейбница.
2. Найти интеграл методом замены переменной.
Вариант 1.
1.  2. а)
2. а)  б)
б) 
Вариант 2.
1. 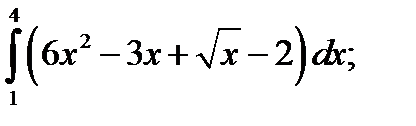 2. а)
2. а) 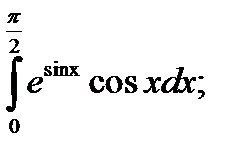 б)
б) 
Вариант 3.
1. 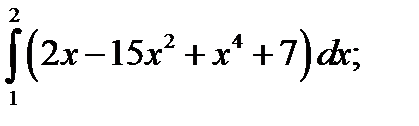 2. а)
2. а)  б)
б) 
Вариант 4.
1. 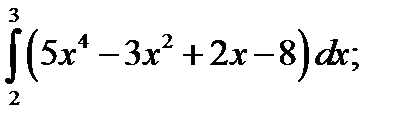 2. а)
2. а)  б)
б) 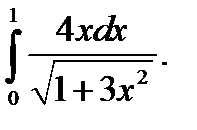
Вариант 5.
1. 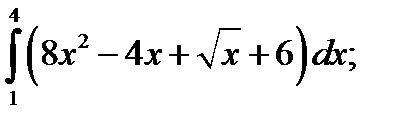 2. а)
2. а) 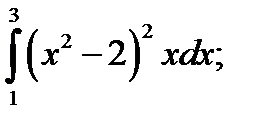 б)
б) 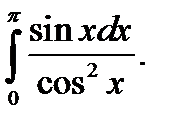
Вариант 6.
1. 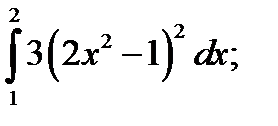 2. а)
2. а) 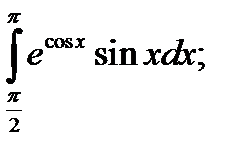 б)
б) 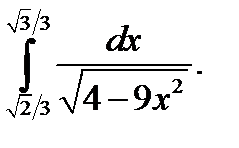
Вариант 7.
1. 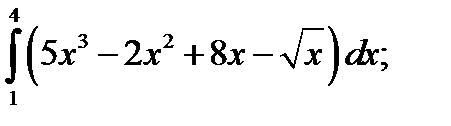 2. а)
2. а) 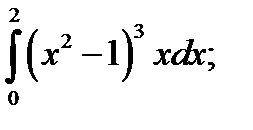 б)
б) 
Вариант 8.
1.  2. а)
2. а) 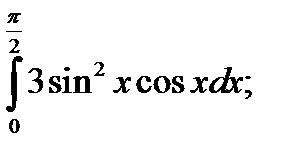 б)
б) 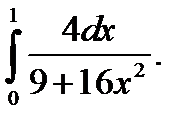
Вариант 9.
1.  2. а)
2. а)  б)
б) 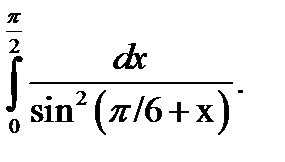
Вариант 10.
1. 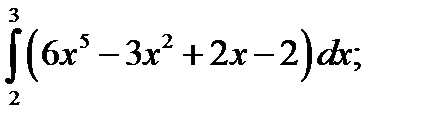 2. а)
2. а) 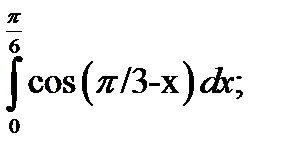 б)
б) 
Вариант 11.
1. 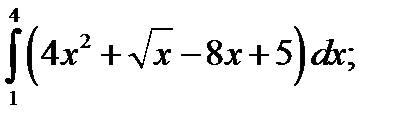 2. а)
2. а) 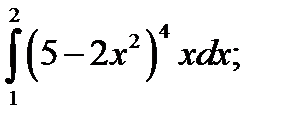 б)
б) 
Вариант 12.
1. 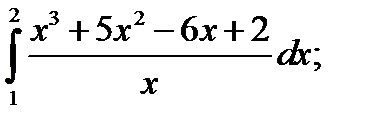 2. а)
2. а)  б)
б) 
Вариант 13.
1.  2. а)
2. а) 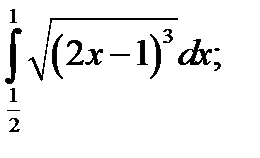 б)
б) 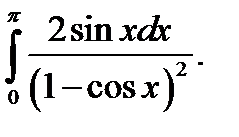
Вариант 14.
1.  2. а)
2. а)  б)
б) 
Вариант 15.
1.  2. а)
2. а) 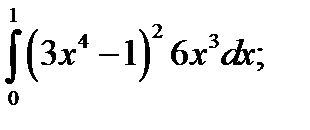 б)
б) 
Вопросы для самоконтроля:
1. Что называют определённым интегралом?
2. Сформулируйте свойства определенного интеграла.
3. Запишите формулу Ньютона - Лейбница.
4. Перечислите основные методы интегрирования.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 17



 где а - нижний предел, b - верхний предел, F ( x )- первообразная функции f ( x ), F ( b )и F ( a )-значения первообразной на концах промежутка.
где а - нижний предел, b - верхний предел, F ( x )- первообразная функции f ( x ), F ( b )и F ( a )-значения первообразной на концах промежутка. 

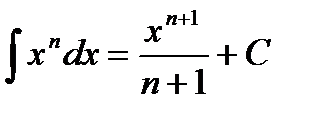 ,
, 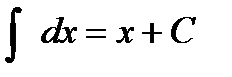 и их свойства получим:
и их свойства получим:
 .
. и вычислим определенный интеграл по формуле
и вычислим определенный интеграл по формуле  :
: 
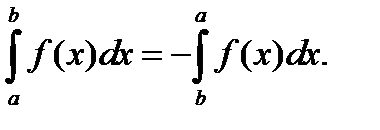

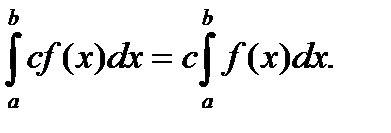
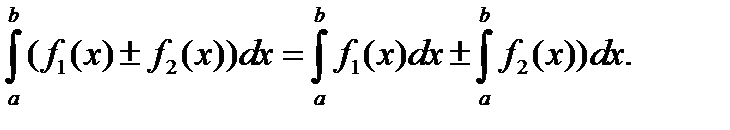
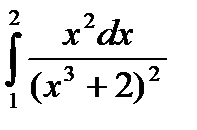 .
.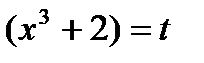 , тогда
, тогда  .
. . При
. При 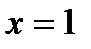 , получаем
, получаем  , при
, при  , находим
, находим 

 .
.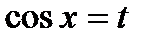 , тогда
, тогда 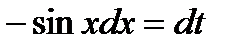 и
и 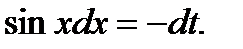
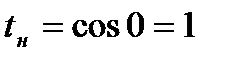 ,
, 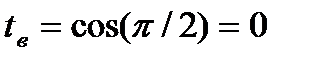 .
.
 .
.
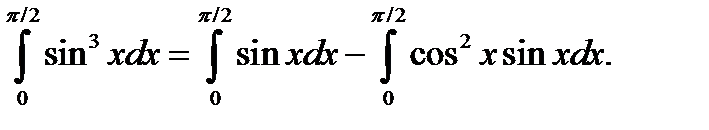


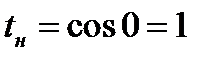 ,
, 
 2. а)
2. а)  б)
б) 
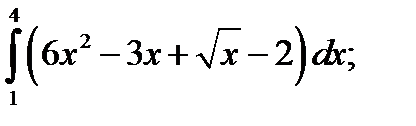 2. а)
2. а) 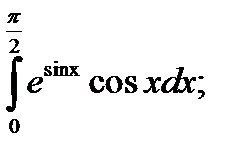 б)
б) 
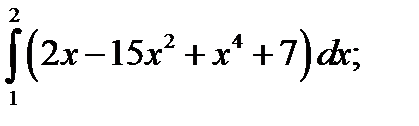 2. а)
2. а)  б)
б) 
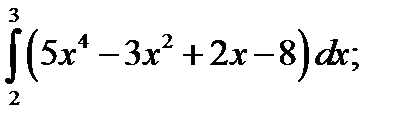 2. а)
2. а)  б)
б) 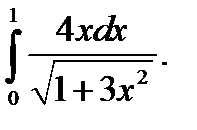
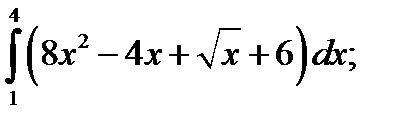 2. а)
2. а) 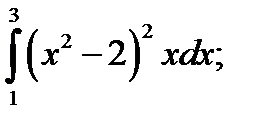 б)
б) 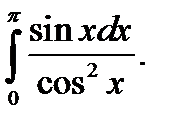
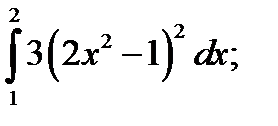 2. а)
2. а) 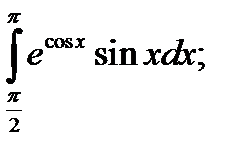 б)
б) 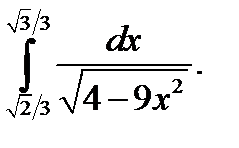
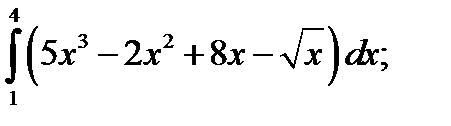 2. а)
2. а) 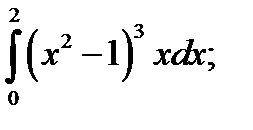 б)
б) 
 2. а)
2. а) 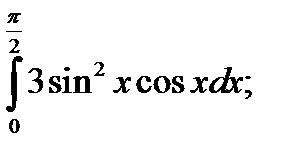 б)
б) 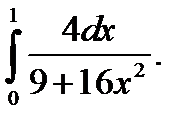
 2. а)
2. а)  б)
б) 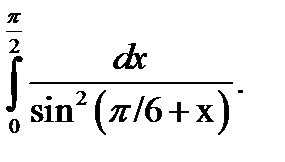
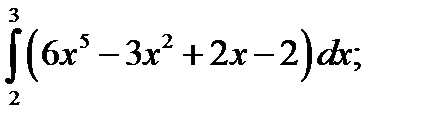 2. а)
2. а) 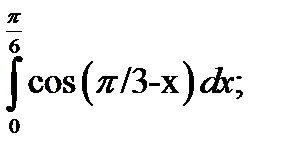 б)
б) 
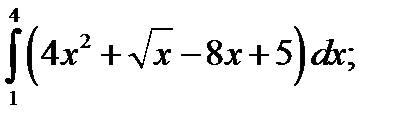 2. а)
2. а) 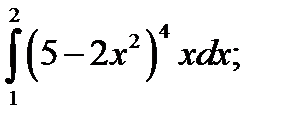 б)
б) 
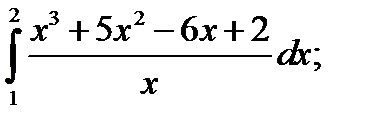 2. а)
2. а)  б)
б) 
 2. а)
2. а) 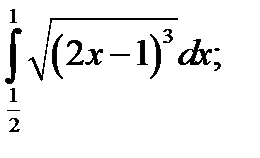 б)
б) 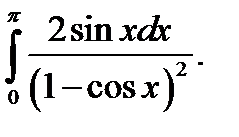
 2. а)
2. а)  б)
б) 
 2. а)
2. а) 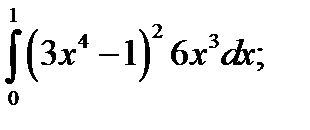 б)
б) 


