В соответствии с тезисом Черта. всякая вычисляемая методом алгоритмов частично рекурсивна.
Мы рассмотрели две модели: р.ф. и м.т.
Функция частично рекурсивна тогда т только тогда когда она может быть вычислена м.т. это математическое утверждение требует док-во.
Док-во рассмотрим в виде 2-х теорем.
Т.1/ Всякая частичная р.ф. вычисляется м.т.
док-во:
Используем определение частично р.ф. таким образом док – во разобьем на сл этапы.
1. Реализация простейшей функции на м.т.
2. Реализация оператора суперпозиций на м.т.
3. Реализация оператора прим. рекурс на м.т.
4. Реализация оператора минимизации на м.т.
1. а) 0(х) – путем стирания всех единиц кроме 1.
б) S(x) –к слову на ленте добавится одна единичка.
в) стираются все палочка и звездочки кроме группы xm подсчет номера группы xm выполняется при использовании соответствующего числа состояний.
2. 
Применяется композиция м.т. при этом 
3. Строится м.т. которая выполняется циклами.
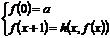
схема более общего вида реализуется аналогично. вычисления осуществляются циклами на ленте.
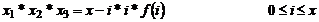
4. опишем реализацию оператора простейшего вида 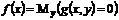 в общем случае реализация аналогична. после цикла i на ленте x*i, если вычисления еще не закончены, в течение (i+1) циклов вычисляется g(x,i) проверяется g(x,i)=0
в общем случае реализация аналогична. после цикла i на ленте x*i, если вычисления еще не закончены, в течение (i+1) циклов вычисляется g(x,i) проверяется g(x,i)=0
Если да то выдается значение i. Если нет то x*i преобразуется в x*i+1
таким образом установлено что простые функции вычислимы по Тьюрингу и если некоторые ф. получена получена из вычислимых ф применением оператора суперпозиций, п.р.ф. и минимизации, то она также вычислима.
Вывод: все частично р.ф. могут быть вычислены м.т.
чтд
Т.2/ Всякая функция вычисляемая на м.т. частично рекурсивна.
Док-во:
Т-м. т. вычисляемая любую функцию f(x) тогда начальная конфигурация.
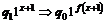
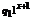 - не останавливается
- не останавливается
(m,j,a,n) – где m,a,n конфигурация на ленте j-обозревается
Для начальной конфигурации m=0; j=1; a=1; n=n(x) (0,1,1,n(x))
Выполним арифметизацию указанным ранее способом тогда n(x) – будет k-ичное слово имеющее следующий вид 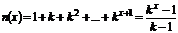
т.к. n(x) – целое число тогда k>1 стараемся перейти к пр. р.ф.
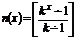 - рекурсивная функция т.к. является суперпозицией пр. р. а значит и рекусивных функций.
- рекурсивная функция т.к. является суперпозицией пр. р. а значит и рекусивных функций.
Обозначим через q(t,x) которая перейдет м. через t тактов используем результат арифмитизации тогда q(t,x) есть 
Аналогично запишем:

 - рекурсивная ф => a(t,x),q(t,x),m(t,x),n(t,x) – рекурсивные ф.
- рекурсивная ф => a(t,x),q(t,x),m(t,x),n(t,x) – рекурсивные ф.
q0=0
обозначим через t0(x) – момент остановки 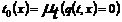
Если ф. вычисляема в м.т. тогда q=q0=0
Если м.т. не остановится. то t0(x) –не определено
таким образом с помощью оператора минимизации получаем частично рекурс ф. t0(x)
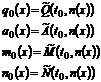
В закл конфигурации.

k>1 и 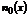 - целое число
- целое число
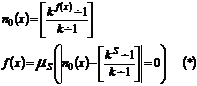
Если удастся вычислить t0(x) тогда определено знач  тогда с помощью (*) находим знач f(x)
тогда с помощью (*) находим знач f(x)
Если t0(x) неопределенна т.е. q0 – не достигается, машина не останавливается => знач f(x) – не определено => f(x) получаемая из (*) частично рекурсивна.
чтд







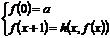
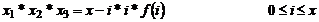
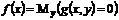 в общем случае реализация аналогична. после цикла i на ленте x*i, если вычисления еще не закончены, в течение (i+1) циклов вычисляется g(x,i) проверяется g(x,i)=0
в общем случае реализация аналогична. после цикла i на ленте x*i, если вычисления еще не закончены, в течение (i+1) циклов вычисляется g(x,i) проверяется g(x,i)=0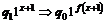
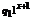 - не останавливается
- не останавливается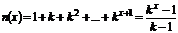
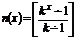 - рекурсивная функция т.к. является суперпозицией пр. р. а значит и рекусивных функций.
- рекурсивная функция т.к. является суперпозицией пр. р. а значит и рекусивных функций.

 - рекурсивная ф => a(t,x),q(t,x),m(t,x),n(t,x) – рекурсивные ф.
- рекурсивная ф => a(t,x),q(t,x),m(t,x),n(t,x) – рекурсивные ф.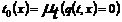
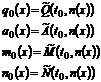

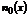 - целое число
- целое число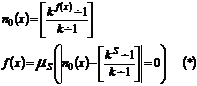
 тогда с помощью (*) находим знач f(x)
тогда с помощью (*) находим знач f(x)


