ТМО-12 ТЕПЛОПРОВОДНОСТЬ ПРИ НЕСТАЦИОНАРНОМ РЕЖИМЕ
Постановка задачи
Рассмотренные ранее процессы стационарной теплопроводности являются по сути дела предельными тепловыми состояниями тел, наступающими при постоянных граничных условиях через продолжительный промежуток времени. Стационарному состоянию предшествует период, в течение которого распределение температур в теле изменяется во времени. (Пример: включение системы отопления, прогрев ограждающей конструкции при tн = const, а затем стационарный процесс теплопередачи через ограждение при tн = const и tв = const).
Если температурное поле нестационарное (изменяется во времени), то тепловые процессы, протекающие в таких условиях, называются нестационарными.
В общем случае уравнение трехмерного нестационарного температурного поля:
t = f (x,y,z,t) (12.1)
Нахождение конкретного вида уравнения (12.1) и является основной задачей нестационарной теплопроводности – поскольку определить изменения теплового потока во времени и пространстве, возможно только зная закон изменения температурного поля.
Уметь определять закономерности изменения температурного поля и теплового потока во времени и пространстве при нестационарной теплопроводности необходимо для решения практических инженерных задач в самых различных отраслях техники:
- при нагреве и охлаждении металлических заготовок;
- при прокаливании твердых тел в производстве стекла, кирпича, керамических изделий;
- при вулканизации резины;
- в отоплении, вентиляции, кондиционировании воздуха, теплогенерирующих установках и т.д.
Пример: ограждения зданий испытывают, изменяющееся во времени (иногда резко), тепловое воздействие, как со стороны наружного воздуха, так и со стороны помещения. В массиве ограждения осуществляется процесс нестационарной теплопроводности.
Формулировка задачи нестационарной теплопроводности включает:
- основное уравнение теплопроводности

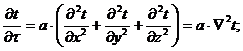 (12.2)
(12.2)
- краевые условия (условия однозначности)
1) начальные условия – задают значение искомой функции t в начальный момент времени, т.е. распределение температур в теле и температуру окружающей среды в начальный момент времени;
2) физические условия – теплофизические параметры тела:

3) геометрические – геометрические размеры тела;
4) граничные - граничные условия формулируют в виде граничных условий III рода, часто встречающихся на практике при постоянной температуре окружающей среды, и одинаковом коэффициенте теплоотдачи по всей поверхности рассматриваемого тела.
Для определенности рассмотрим в качестве тела, в котором необходимо найти температурное поле прямоугольный параллелепипед с размерами граней 2d; 2l
y; 2l
z.






























Рисунок 12.1 Формулировка задачи нестационарной теплопроводности для прямоугольного параллелепипеда
Если начало декартовой системы координат расположить в центре симметрии параллелепипеда, то:
1) начальные условия запишутся в виде:
при t = 0, t0 = f (x,y,z,); (12.3)
2) физические - заданы l, Ср, r тела; (12.4)
3) геометрические - - d £ х £ + d; - ly £ у £ +ly; - lz £ z £ +lz; (12.5)
4) граничные условия III рода при t > 0, одинаковом коэффициенте теплоотдачи a по всей поверхности тела и постоянной заданной величине температуры окружающей среды – tср можно записать в виде:

 (12.6)
(12.6)

Температура в каждом из трех приведенных уравнений берется на соответствующей грани параллелепипеда, (например: для первого уравнения на двух гранях нормальных к оси х и отстоящих от 0 на расстоянии d).
Задача процесса нестационарной теплопроводности в теле приведенного параллелепипеда сформулирована в уравнениях – 2, 3, 4, 5, 6.
Её можно решить аналитически, т.е. путем алгебраических преобразований, дифференцирования, интегрирования и т.д. В результате может быть получена формула для расчета температурного поля: t = f (x,y,z,t).
В большинстве практически важных случаев аналитического решения сформулированной системы уравнений получить нельзя, поэтому стараются упростить задачу и применяют численные методы, которые для задач теплопроводности проработаны весьма фундаментально.
Неограниченная пластина
Находится аналитическое решение сформулированной выше задачи в одномерном варианте, т.е. требуется найти уравнение температурного поля вида: t = f (x,t).








Рисунок 12.2 Плоскопараллельная пластина бесконечной длины и высоты
- Рассматривается охлаждение плоскопараллельной пластины, размеры которой в направлении осей 0Z и 0Y бесконечно велики, а толщина равна 2d.
- Пластина помещена в среду с постоянной температурой – tср (или ее обозначают tж);
- Коэффициент теплоотдачи с обеих сторон пластины имеет одинаковое и постоянное значение (a).
Так как ly >> 2d и lz >> 2d, то дифференциальное уравнение (12.2) принимает вид:
 ; (12.7)
; (12.7)
Условия однозначности для рассматриваемого случая:
1) Начальные условия
В начальный момент времени пластина имеет во всех точках постоянную температуру: при t = 0; tо = const, а превышение температуры пластины над температурой среды (в случае ее охлаждения): J1 = tо - tср, (начальная избыточная температура).
2) Физические условия
Задан коэффициент температуропроводности материала пластины: 
3) Геометрические условия
- d £ х £ +d;
4) Граничные условия III рода при t > 0
 (*)
(*)
Сформулируем поставленную задачу в безразмерных переменных:
Безразмерная температура:
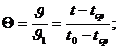 (12.8)
(12.8)
J1= t0 - tср – избыточная температура в начале процесса при t = 0;
J = t - tср – текущая избыточная температура при t > 0;
Безразмерная координата:
C= х /d: (12.9)
Подставив эти величины в уравнение (12.7), получим:
 (12.10)
(12.10)
где  - число Фурье – «безразмерное время».
- число Фурье – «безразмерное время».
Начальные условия при t = 0;
Fo = 0 Þ Q = 1, так как J = J1
Граничные условия: при t > 0; Fo > 0 и C = 1 уравнение (*) запишется в виде:
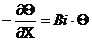 ; (12.11)
; (12.11)
где  Þ критерий Био.
Þ критерий Био.
Формулировка этой задачи в безразмерном виде содержит единственный параметр критерий Био.
Критерий – потому, что, составлен из величин, входящих в условия однозначности.
Формально критерий Био сходен с числом Нуссельта 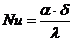 . Сходство именно формальное, т.к.:
. Сходство именно формальное, т.к.:
- использование критерия Био связано с нахождением температурного поля в твердом теле, поэтому в знаменателе – коэффициент теплопроводности твердого тела lст. Число Nu связано с температурным полем жидкости – в знаменателе коэффициент теплопроводности жидкости l.
- критерий Био – наперед заданный параметр. Число Nu – искомая величина.
В результате решения составленной в безразмерном виде системы уравнений (12.8, 12.9, 12.10, 12.11) температура поверхности стенки пластины (tст) и температура в центральной плоскости пластины (tц) определятся из соотношений:
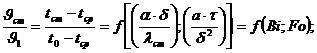 (12.12)
(12.12)
 (12.13)
(12.13)
Jст = tст – tcр, - текущая избыточная температура стенки пластины по сравнению с температурой среды, оС;
Jц = tц – tcр, - текущая избыточная температура центра пластины по сравнению с температурой среды, оС;
Эти выражения справедливы и при нагреве и при остывании пластины, т.е и при tо < tcр, и при tо > tcр.
Количество теплоты, которое отдает (или воспринимает) пластина в окружающую среду за время t, должно равняться изменению её внутренней энергии за период её охлаждения (или нагревания).
Начальная внутренняя энергия пластины, отсчитанная от её же внутренней энергии при температуре среды, окружающей стенку, как от нуля, равна:
Qo = 2d×F×cp×r×(t0 - tcp) = 2d×F×cp×r×J1, Дж (12.14)
F – площадь боковой поверхности пластины, м2;
Qо – «избыточная» внутренняя энергия пластины, (в случае охлаждения).
Введение этой величины необходимо для приведения теплового потока к безразмерному виду.
Количество теплоты, выделившееся в окружающую среду за время τ:
 Qτ = 2d×F×cp×r×(t0 - tcт), Дж (12.15)
Qτ = 2d×F×cp×r×(t0 - tcт), Дж (12.15)
 tcт – средняя температура стенки по истечении времени τ.
tcт – средняя температура стенки по истечении времени τ.
Количество теплоты, выделяющееся при охлаждении пластины за время τ, определится из выражения:
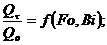 (12.16)
(12.16)
Зависимости 12.12, 12.13 и 12.16 даются в виде графиков (номограмм) и таблиц, причем последние точнее.
Как правило, начальная температура тела tо и температура среды tcр – заданы. Вначале вычисляют Fo и Bi, по которым определяют: 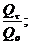

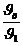 , а затем tcт, tц и Qτ.
, а затем tcт, tц и Qτ.
Как было показано выше уравнения (12.9), (12.10) и (12.11) формулируют задачу нестационарной теплопроводности в безразмерном виде.
Если рассматривать два процесса нестационарной теплопроводности с одинаковыми числами Bi, т.е Bi 1 = Bi 2 то, согласно третьей теореме подобия, эти процессы подобны. Это значит, что в сходственных точках, т.е. при C 1 = C 2; Fo 1 = Fo 2 безразмерные температуры будут численно равны Θ1 = Θ2.
Следовательно, произведя один расчет температурного поля в безразмерном виде, мы получим результат справедливый для всего класса подобных явлений, которые могут различаться размерными параметрами: а, α, λ, δ, t0, tcp.
Например, класс явлений нестационарной теплопроводности при охлаждении (нагревании) плоско-параллельной пластины:
Θ = f (Fo, Bi, C), т.к. Bi – задано, то: Θ = f (Fo, C).
Охлаждение параллелепипеда
Рассмотрим охлаждение параллелепипеда в среде с постоянной температурой (t
ср) и с постоянным коэффициентом теплоотдачи a на всех его гранях. В начальный момент времени (t=0) все точки параллелепипеда имеют одинаковую температуру (t
0).












Рисунок 12.7 К охлаждению параллелепипеда
Параллелепипед c размерами 2dx ´ 2dу ´ 2dz является однородным и изотропным.
Требуется найти распределение температуры в параллелепипеде для любого момента времени, а также среднюю температуру, необходимую для определения количества отведенной (подведенной) теплоты.
Поместим начало координат в центре параллелепипеда. При этом дифференциальное уравнение запишется следующим образом:

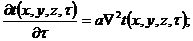 (12.40)
(12.40)
Нахождение аналитического решения этого уравнения, дополненного условиями однозначности, представляет собой довольно сложную задачу.
Параллелепипед конечных размеров можно рассматривать как тело, образованное пересечением соответственно трех взаимно перпендикулярных неограниченных пластин конечной толщины.
Доказано, что решение таких задач представляется произведением безразмерных температур для тел неограниченных размеров, в результате пересечения которых образовалось рассматриваемое тело.
Параллелепипед образован в результате пересечения трех взаимно перпендикулярных неограниченных пластин конечными толщинами 2dx, 2dу, 2dz. Следовательно, для него и решение можно представить как произведение безразмерных температур для трех безграничных пластин:
Q = Qx × Qy × Qz (12.41)
Множители в уравнении (12.41) могут быть рассчитаны по уравнению (12.20) или определены по номограммам.
Этот метод известен в теории теплопроводности под названием теоремы о перемножении решений.
Полученное решение справедливо и для нахождения средней температуры:
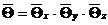 (12.42)
(12.42)
Множители в уравнении (12.42) находятся по формуле (12.27).
12.8.2 Охлаждение (нагревание) длинного прямоугольного стержня
Поперечное сечение стержня представляет собой прямоугольник с размерами 2δх × 2δу. Такое тело можно рассматривать как результат взаимного пересечения двух неограниченных пластин толщиной 2δх и 2δу, условия однозначности для которых такие же, как и для образовавшегося стержня. Безразмерное температурное поле для поставленной задачи:
Q = Qx × Qy (12.43)
Множители в уравнении (12.43) также могут быть рассчитаны по уравнению (12.20) или определены по номограммам.

Рисунок 12.8 К охлаждению полуограниченного прямоугольного стержня
12.8.3 Охлаждение цилиндра конечной длины

Рисунок 12.9 К охлаждению цилиндра конечной длины
Цилиндр конечной длины можно рассматривать как результат пересечения безграничного цилиндра радиусом r0 и пластины толщиной 2δZ. Следовательно, и безразмерную температуру для такого тела можно записать как:
Q = Qr × Qz (12.44)
Полученные решения для полуограниченного прямоугольного стержня и цилиндра конечной длины (формулы 12.43 и 12.44) справедливы и для нахождения средних температур.
Кроме того, следует подчеркнуть, что все решения, полученные выше справедливы как для охлаждения, так и для нагрева тел неограниченных и конечных размеров.
ТМО-12 ТЕПЛОПРОВОДНОСТЬ ПРИ НЕСТАЦИОНАРНОМ РЕЖИМЕ
Постановка задачи
Рассмотренные ранее процессы стационарной теплопроводности являются по сути дела предельными тепловыми состояниями тел, наступающими при постоянных граничных условиях через продолжительный промежуток времени. Стационарному состоянию предшествует период, в течение которого распределение температур в теле изменяется во времени. (Пример: включение системы отопления, прогрев ограждающей конструкции при tн = const, а затем стационарный процесс теплопередачи через ограждение при tн = const и tв = const).
Если температурное поле нестационарное (изменяется во времени), то тепловые процессы, протекающие в таких условиях, называются нестационарными.
В общем случае уравнение трехмерного нестационарного температурного поля:
t = f (x,y,z,t) (12.1)
Нахождение конкретного вида уравнения (12.1) и является основной задачей нестационарной теплопроводности – поскольку определить изменения теплового потока во времени и пространстве, возможно только зная закон изменения температурного поля.
Уметь определять закономерности изменения температурного поля и теплового потока во времени и пространстве при нестационарной теплопроводности необходимо для решения практических инженерных задач в самых различных отраслях техники:
- при нагреве и охлаждении металлических заготовок;
- при прокаливании твердых тел в производстве стекла, кирпича, керамических изделий;
- при вулканизации резины;
- в отоплении, вентиляции, кондиционировании воздуха, теплогенерирующих установках и т.д.
Пример: ограждения зданий испытывают, изменяющееся во времени (иногда резко), тепловое воздействие, как со стороны наружного воздуха, так и со стороны помещения. В массиве ограждения осуществляется процесс нестационарной теплопроводности.
Формулировка задачи нестационарной теплопроводности включает:
- основное уравнение теплопроводности

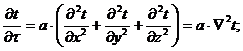 (12.2)
(12.2)
- краевые условия (условия однозначности)
1) начальные условия – задают значение искомой функции t в начальный момент времени, т.е. распределение температур в теле и температуру окружающей среды в начальный момент времени;
2) физические условия – теплофизические параметры тела:

3) геометрические – геометрические размеры тела;
4) граничные - граничные условия формулируют в виде граничных условий III рода, часто встречающихся на практике при постоянной температуре окружающей среды, и одинаковом коэффициенте теплоотдачи по всей поверхности рассматриваемого тела.
Для определенности рассмотрим в качестве тела, в котором необходимо найти температурное поле прямоугольный параллелепипед с размерами граней 2d; 2l
y; 2l
z.















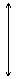





















Рисунок 12.1 Формулировка задачи нестационарной теплопроводности для прямоугольного параллелепипеда
Если начало декартовой системы координат расположить в центре симметрии параллелепипеда, то:
1) начальные условия запишутся в виде:
при t = 0, t0 = f (x,y,z,); (12.3)
2) физические - заданы l, Ср, r тела; (12.4)
3) геометрические - - d £ х £ + d; - ly £ у £ +ly; - lz £ z £ +lz; (12.5)
4) граничные условия III рода при t > 0, одинаковом коэффициенте теплоотдачи a по всей поверхности тела и постоянной заданной величине температуры окружающей среды – tср можно записать в виде:

 (12.6)
(12.6)

Температура в каждом из трех приведенных уравнений берется на соответствующей грани параллелепипеда, (например: для первого уравнения на двух гранях нормальных к оси х и отстоящих от 0 на расстоянии d).
Задача процесса нестационарной теплопроводности в теле приведенного параллелепипеда сформулирована в уравнениях – 2, 3, 4, 5, 6.
Её можно решить аналитически, т.е. путем алгебраических преобразований, дифференцирования, интегрирования и т.д. В результате может быть получена формула для расчета температурного поля: t = f (x,y,z,t).
В большинстве практически важных случаев аналитического решения сформулированной системы уравнений получить нельзя, поэтому стараются упростить задачу и применяют численные методы, которые для задач теплопроводности проработаны весьма фундаментально.
Неограниченная пластина
Находится аналитическое решение сформулированной выше задачи в одномерном варианте, т.е. требуется найти уравнение температурного поля вида: t = f (x,t).








Рисунок 12.2 Плоскопараллельная пластина бесконечной длины и высоты
- Рассматривается охлаждение плоскопараллельной пластины, размеры которой в направлении осей 0Z и 0Y бесконечно велики, а толщина равна 2d.
- Пластина помещена в среду с постоянной температурой – tср (или ее обозначают tж);
- Коэффициент теплоотдачи с обеих сторон пластины имеет одинаковое и постоянное значение (a).
Так как ly >> 2d и lz >> 2d, то дифференциальное уравнение (12.2) принимает вид:
 ; (12.7)
; (12.7)
Условия однозначности для рассматриваемого случая:
1) Начальные условия
В начальный момент времени пластина имеет во всех точках постоянную температуру: при t = 0; tо = const, а превышение температуры пластины над температурой среды (в случае ее охлаждения): J1 = tо - tср, (начальная избыточная температура).
2) Физические условия
Задан коэффициент температуропроводности материала пластины: 
3) Геометрические условия
- d £ х £ +d;
4) Граничные условия III рода при t > 0
 (*)
(*)
Сформулируем поставленную задачу в безразмерных переменных:
Безразмерная температура:
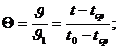 (12.8)
(12.8)
J1= t0 - tср – избыточная температура в начале процесса при t = 0;
J = t - tср – текущая избыточная температура при t > 0;
Безразмерная координата:
C= х /d: (12.9)
Подставив эти величины в уравнение (12.7), получим:
 (12.10)
(12.10)
где  - число Фурье – «безразмерное время».
- число Фурье – «безразмерное время».
Начальные условия при t = 0;
Fo = 0 Þ Q = 1, так как J = J1
Граничные условия: при t > 0; Fo > 0 и C = 1 уравнение (*) запишется в виде:
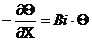 ; (12.11)
; (12.11)
где  Þ критерий Био.
Þ критерий Био.
Формулировка этой задачи в безразмерном виде содержит единственный параметр критерий Био.
Критерий – потому, что, составлен из величин, входящих в условия однозначности.
Формально критерий Био сходен с числом Нуссельта 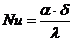 . Сходство именно формальное, т.к.:
. Сходство именно формальное, т.к.:
- использование критерия Био связано с нахождением температурного поля в твердом теле, поэтому в знаменателе – коэффициент теплопроводности твердого тела lст. Число Nu связано с температурным полем жидкости – в знаменателе коэффициент теплопроводности жидкости l.
- критерий Био – наперед заданный параметр. Число Nu – искомая величина.
В результате решения составленной в безразмерном виде системы уравнений (12.8, 12.9, 12.10, 12.11) температура поверхности стенки пластины (tст) и температура в центральной плоскости пластины (tц) определятся из соотн<




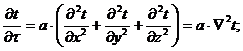 (12.2)
(12.2)
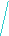




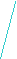
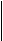

































 (12.6)
(12.6)








 ; (12.7)
; (12.7) (*)
(*)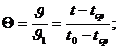 (12.8)
(12.8) (12.10)
(12.10) - число Фурье – «безразмерное время».
- число Фурье – «безразмерное время».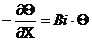 ; (12.11)
; (12.11) Þ критерий Био.
Þ критерий Био.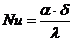 . Сходство именно формальное, т.к.:
. Сходство именно формальное, т.к.: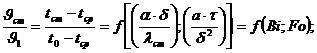 (12.12)
(12.12) (12.13)
(12.13) Qτ = 2d×F×cp×r×(t0 - tcт), Дж (12.15)
Qτ = 2d×F×cp×r×(t0 - tcт), Дж (12.15) tcт – средняя температура стенки по истечении времени τ.
tcт – средняя температура стенки по истечении времени τ.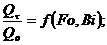 (12.16)
(12.16)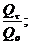

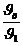 , а затем tcт, tц и Qτ.
, а затем tcт, tц и Qτ. Рассмотрим охлаждение параллелепипеда в среде с постоянной температурой (tср) и с постоянным коэффициентом теплоотдачи a на всех его гранях. В начальный момент времени (t=0) все точки параллелепипеда имеют одинаковую температуру (t0).
Рассмотрим охлаждение параллелепипеда в среде с постоянной температурой (tср) и с постоянным коэффициентом теплоотдачи a на всех его гранях. В начальный момент времени (t=0) все точки параллелепипеда имеют одинаковую температуру (t0).

















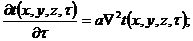 (12.40)
(12.40) (12.42)
(12.42)