Оценка неизвестной вероятности случайного события
Задачи математической статистики связаны с неизвестностью распределения наблюдений. Но распределение — это совокупность вероятностей, поэтому начнем с оценки неизвестной вероятности.
Пусть A — случайное событие, p = P(A) — его неизвестная вероятность. Пусть проведено n испытаний этого события, n — количество появления события А, т.е. количество успехов. Рассмотрим в качестве оценки для p статистику
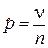 , (1)
, (1)
где 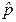 — относительная частота появления события А. случайная величина n распределена по биномиальному закону Bi (n, p), и потому
— относительная частота появления события А. случайная величина n распределена по биномиальному закону Bi (n, p), и потому
 .
.
Это означает, что оценка 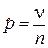 несмещённая. Проверим состоятельность оценки:
несмещённая. Проверим состоятельность оценки:
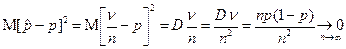 ,
,
где D — дисперсия. Т.е. оценка состоятельна.
Оценка неизвестной функции распределения. Основная теорема статистики
Пусть имеется выборка x1, ξ2…xn с неизвестной функцией распределения F (x). Построим оценку для F (x). Зафиксируем произвольное значение аргумента х. Значение F (x) в точке x есть вероятность события Ах= {x< х }, т.е. F (x) = P (A x). Несмещённой и состоятельной оценкой для вероятности P (A x) — она же и оценка 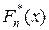 для F (x) — является относительная частота (см. пример в п. 2.1):
для F (x) — является относительная частота (см. пример в п. 2.1):

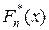 =
= 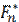 (x; x1, ξ2…xn), (2)
(x; x1, ξ2…xn), (2)
где nх — количество появления события Ах в n испытаниях, т. е. количество тех наблюдений x i в выборке, которые меньше х (xi < x). Случайная величина nх имеет биномиальное распределение Bi (n, F (x)) с параметрами n и F (x). Имеет место несмещённость:
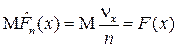
Также справедлива состоятельность:
 .
.
Итак, при любом х оценка (2) является несмещённой и состоятельной.
Функция 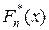 ≡
≡ 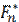 (x | x1, ξ2…xn) называется ФУНКЦИЕЙ ЭМПИРИЧЕСКОГО РАСПРЕДЕЛЕНИЯ (основное понятие семестра)
(x | x1, ξ2…xn) называется ФУНКЦИЕЙ ЭМПИРИЧЕСКОГО РАСПРЕДЕЛЕНИЯ (основное понятие семестра)
основная теорема статистики. Функция эмпирического распределения сходится (по вероятности) к истинной функции распределения:
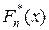 ≡
≡ 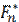 (x; x1, ξ2…xn)
(x; x1, ξ2…xn) 
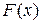 . (3)
. (3)
 Справедливость этого утверждения показана предыдущими соотношениями. График функции эмпирического распределения показан на рис. 1:
Справедливость этого утверждения показана предыдущими соотношениями. График функции эмпирического распределения показан на рис. 1: 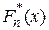 кусочно-постоянная, делает скачок величиной 1/ n, когда аргумент x при его возрастании переходит выборочное значение.
кусочно-постоянная, делает скачок величиной 1/ n, когда аргумент x при его возрастании переходит выборочное значение.
Рис. 1. Функция эмпирического Заметим, что если в n точках x1, ξ2…xn
распределения на оси х поместить равные вероятности 1/ n, то получится некоторое дискретное распределение, называемое эмпирическим, и 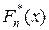 — его функция распределения. Ясно, что первые два момента этого распределения таковы:
— его функция распределения. Ясно, что первые два момента этого распределения таковы:
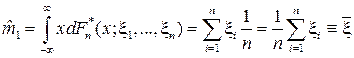 , (4)
, (4)
 .
.
В этих равенствах учтено, что при кусочно-постоянной интегрирующей функции интеграл Стильтьеса превращается в сумму. Второй центральный момент эмпирического распределения:
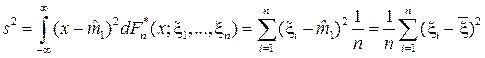 . (5)
. (5)
Статистика 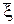 называется выборочным средним, а s2 — выборочной дисперсией.
называется выборочным средним, а s2 — выборочной дисперсией.
Простейшие оценки моментов
Пусть имеется выборка x1,ξ2…xn. Функция распределения F (x) наблюдений нам неизвестна.
А. оценка математического ожидания.
По определению математическое ожидание (первый момент) есть
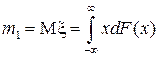 .
.
Подставим в интеграл вместо F (x) несмещенную и состоятельную оценку  (x | x1, ξ2…xn). Получим (4):
(x | x1, ξ2…xn). Получим (4):
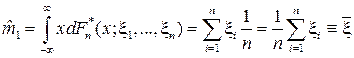
Получили (4)-дисперсию эмпирического распределения
 .
.
Рассмотрим эту статистику в качестве оценки для математического ожидания m 1. Проверим несмещённость:
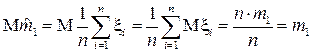 .
.
Проверим состоятельность:
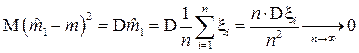 .
.
Таким образом, 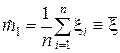 является несмещенной и состоятельной оценкой для математического ожидания.
является несмещенной и состоятельной оценкой для математического ожидания.
Заметим, что замена истинного неизвестного нам распределения эмпирическим (или выборочным) приводит к состоятельным оценкам.
Кроме того, заметим, что проверка на несмещенность и состоятельность являются стандартными действиями
Б. Оценка дисперсии.
Дисперсия случайной величины, согласно определению:
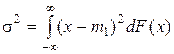 .
.
Вместо неизвестных m 1 и F (x) подставим состоятельные оценки 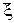 и
и 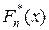 .
.
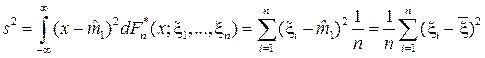
Получили оценку s 2 для s2 (формула (5) выше):
s 2 = 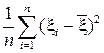 .
.
Проверим несмещённость, для чего сначала преобразуем выражение для s2:
s 2 =  =
=
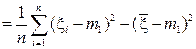 . (5а)
. (5а)
Здесь учтено, что 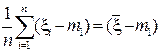 . Определим математическое ожидание:
. Определим математическое ожидание:
М s 2 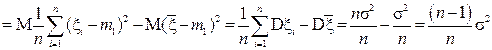 ¹s2.
¹s2.
Оно не равно s2, и потому оценка смещенная. Ясно, что ее можно исправить, умножив s 2 на константу, обратную к коэффициенту при s2. Рассмотрим исправленную оценку
s 12 =  s 2 =
s 2 = 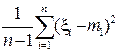 .
.
Эта оценка является несмещенной:
M s 12 =  M s 2 = s2.
M s 2 = s2.
Обе оценки s 2 и s 12 являются состоятельными, что видно из (5а), используя свойства сходимости по вероятности, аналогичные свойствам сходимости числовых последовательностей.
В. Оценка моментов порядка k > 2.
Для начального момента порядка k > 2
mk = Mx k = 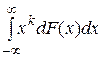 ,
,
рассмотрим оценку, полученную заменой F (x) на  (x | x1, ξ2…xn):
(x | x1, ξ2…xn):
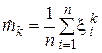 .
.
Она является несмещенной:
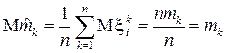 .
.
Можно показать, что оценка состоятельна, т.е.
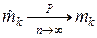 .
.
Для центрального момента порядка k > 2
m k = M(x - m1) k = 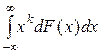 ,
,
рассмотрим оценку, полученную аналогично предыдущему:
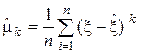 .
.
Можно показать, что данная оценка состоятельна, т.е.
 ,
,
но несмещенной она не является. И исправить ее, аналогично выборочной дисперсии, умножением на коэффициент, зависящий от n, невозможно.



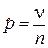 , (1)
, (1)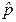 — относительная частота появления события А. случайная величина n распределена по биномиальному закону Bi (n, p), и потому
— относительная частота появления события А. случайная величина n распределена по биномиальному закону Bi (n, p), и потому .
.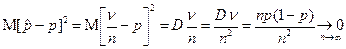 ,
,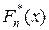 для F (x) — является относительная частота (см. пример в п. 2.1):
для F (x) — является относительная частота (см. пример в п. 2.1):
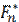 (x; x1, ξ2…xn), (2)
(x; x1, ξ2…xn), (2)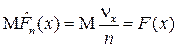
 .
. 
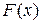 . (3)
. (3) Справедливость этого утверждения показана предыдущими соотношениями. График функции эмпирического распределения показан на рис. 1:
Справедливость этого утверждения показана предыдущими соотношениями. График функции эмпирического распределения показан на рис. 1: 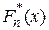 кусочно-постоянная, делает скачок величиной 1/ n, когда аргумент x при его возрастании переходит выборочное значение.
кусочно-постоянная, делает скачок величиной 1/ n, когда аргумент x при его возрастании переходит выборочное значение.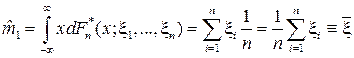 , (4)
, (4) .
.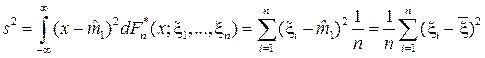 . (5)
. (5)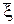 называется выборочным средним, а s2 — выборочной дисперсией.
называется выборочным средним, а s2 — выборочной дисперсией.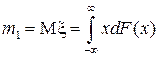 .
. (x | x1, ξ2…xn). Получим (4):
(x | x1, ξ2…xn). Получим (4): .
.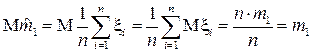 .
.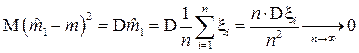 .
.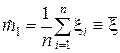 является несмещенной и состоятельной оценкой для математического ожидания.
является несмещенной и состоятельной оценкой для математического ожидания.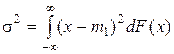 .
.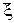 и
и 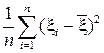 .
. =
=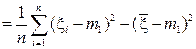 . (5а)
. (5а)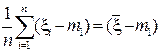 . Определим математическое ожидание:
. Определим математическое ожидание: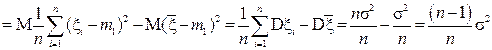 ¹s2.
¹s2. s 2 =
s 2 = 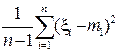 .
.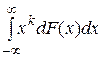 ,
,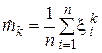 .
.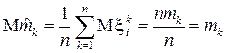 .
.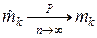 .
.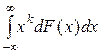 ,
,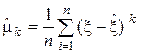 .
. ,
,

