МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
В ТВ (в прошлом семестре) мы определяли вероятности появления различных случайных событий; закон распределения случайных факторов считали известным. В МС решается обратная задача: по наблюдаемым случайным событиям нужно сделать какие либо выводы о неизвестном законе распределения действующих случайных факторов.
Рассуждения в МС основываются на знании теории вероятностей, без уверенного знания основ которой невозможно освоить методы МС. Поэтому необходимо иметь под рукой лекции по ТВ, записи практических занятий и учебные пособия по ТВ.
----------------------------------------
Литература по МС, которая потребуется:
1. Ивченко, Медведев. Математическая статистика (есть и интернете, любое издание годится)
2. Горицкий Ю.А. Основы математической статистики. – М.: МЭИ, 2018, 84с. (есть в библиотеке МЭИ, к киоске МЭИ тоже было; лекции по этому пособию)
3. Сборник задач по математике. Теория вероятностей и математическая статистика. Под редакцией А.В. Ефимова. М.: Физматлит, 1990. (уже знакомый задачник, для решения домашних задач, есть в интернете, в библиотеке МЭИ-тоже)
4. Ю.А. Горицкий, Е.Е. Перцов. Практикум по статистике с пакетами STATGRAPHICS, STATISTICA, SPSS. М. МЭИ, 1997. 85 с.
(для лаб работ, есть в библиотеке МЭИ, кроме того, есть в интернете на Exponenta.ru)
5. Ю.А. Горицкий. Практикум по статистике с пакетом STATISTICA. М. МЭИ, 2000. 79 с. (аналогично п.4)
Все занятия будем проводить в системе Webex.
Содержание занятий
1. Лекции (1 раз в неделю)
2. Практические занятия ( по первым неделям )
3. Лаб работы (7 ЛР) ( по вторым неделям, с пакетом STATISTICA, версия 5.5а). Просьба ко всем поставить этот пакет, он бесплатный.
По каждой работе будет отмечаться: «выполнено», «отчет сделан», «защита по теме ЛР»
4. Контрольная работа «Оценки и доверительные интервалы» (9 неделя)
Зачет
Экзамен за 2 семестра
Лекция 1
ВВЕДЕНИЕ
В МС предполагается:
имеются наблюдения x º (x1, x2 … x n) случайного характера, (не обязательно числовые, могут быть, например, синий, зеленый, ….)
закон распределения частично или полностью неизвестен.
По наблюдениям нужно сделать те или иные выводы относительно неизвестного распределения.
Примеры:
1. Совокупность изделий, доля дефектных неизвестна, наудачу выбрали n штук и проверили, получили результаты: хороший (0), дефектный (1), и т. д.; неизвестная доля дефектных определяет закон распределения наших наблюдений (вероятность 0 и 1), эту долю и нужно определить.
2. Радиолокатор n раз со случайными ошибками измеряет расстояние до движущегося объекта, скорость неизвестна; по наблюдениям нужно определить скорость. Скорость определяет закон распределения измерений.
3. Новое лекарство, есть две группы испытуемых: одной дали новое, другой-старое, посмотрели результаты. Вопрос: новое лучше старого или нет? Результаты случайны, закон распределения (выздоровление или нет, определяется неизвестной вероятностью успеха)
…и.т.д.………
Задачи МС можно условно разделить на три типа:
— оценить неизвестные параметры (теория точечного оценивания);
— указать интервалы, в которых находятся неизвестные параметры (теория интервального оценивания);
— ответить на вопрос: можно ли считать, что неизвестное распределение обладает тем или иным свойством (теория проверки статистических гипотез) примеры вопросов:
- находится ли неизвестный параметр в заданном диапазоне, или нет?
- принадлежит ли неизвестный закон распределения заданному классу или нет?
- зависимы ли два признака у наблюдаемых объектов или нет? (например,форма сбственности влияет на рентабельность производства или нет? есть n наблюдений)
При рассмотрении любой статистической задачи имеющиеся наблюдения x º (x 1, x 2… x n) являются конкретными значениями многомерной случайной величины x º (x1, x2…xn). Мы должны отвлечься от конкретных значений x º (x 1, x 2… x n), нужно считать, что имеем дело со случайной вечичиной x º (x1, x2…xn) (т.е. с совокупностью возможных значений),
и потому способ обработки, который мы конструируем, должен быть «хорошим» (в некотором смысле) для всей совокупности возможных значений, а не только для имеющихся наблюдений.
Глава 1. Оценивание неизвестных параметров
Основные понятия и характеристики качества оценок
В большинстве задач математической статистики предполагается, что наблюдения (x1, x2…xn) являются независимыми, одинаково распределенными случайными величинами с функцией распределения F (x), которая является частично или полностью неизвестной. Вэтом случае они называются ВЫБОРКОЙ объема n из совокупности, распределенной по F (x). Выборка — объект случайный.
Закон распределения выборки легко определяется. Например, для непрерывного случая, если 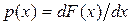 — плотность распределения одной компоненты, то плотность распределения выборки есть
— плотность распределения одной компоненты, то плотность распределения выборки есть
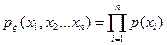 .
.
Любая функция наблюдений j(x1, ξ2…xn) (произвольной размерности) называется СТАТИСТИКОЙ. Примеры статистик:
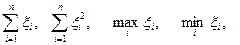
 .
.
Пусть x1, x2…xn — выборка из совокупности, распределённой по закону с функцией распределения F (x; a), зависящей от параметра а. Параметр а неизвестен, его необходимо оценить по выборке x1, ξ2…xn.
Функция наблюдений â = φ(ξ1, ξ2…ξn), с помощью которой оценивается неизвестный параметр, называется ОЦЕНКОЙ или ОЦЕНИВАЮЩЕЙ ФУНКЦИЕЙ. Заметим, что результат применения оценки â = φ(ξ1, ξ2…ξn) является случайной величиной.
Укажем те качества, которыми характеризуется оценка (оценивающая функция).
1. Несмещённость.
Оценка â = φ(ξ1, ξ2…ξn) называется несмещённой, если при любом значении параметра а
Мj = а,
где М — математическое ожидание. В противном случае оценка называется смещенной, и
Мφ – а ≡ b(а)
называется смещением.
Выпишем условие несмещённости в интегральном виде для случая непрерывного распределения:
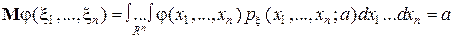 ,
,
где 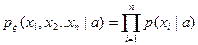 — плотность распределения выборки.
— плотность распределения выборки.
Обозначим ошибку оценки
δn = φ(ξ1, ξ2…ξn) – a.
В терминах ошибки несмещённость означает, что среднее значение ошибки равно нулю, т.е. при любом значении параметра а
Mδn = Мφ – а = 0.
2. Состоятельность.
Оценка â = φ(ξ1, ξ2…ξn) называется состоятельной, если
φ(ξ1, ξ2…ξn) ® a (по вероятности) при n ® ¥
при любом значении а.
В терминах ошибки d n состоятельность означает, что dn сходится к нулю по вероятности при любом значении а:
dn  0,
0,
т.е. для любого сколь угодно малого
e > 0 P{|dn| < e} ® 1.
Проверять состоятельность можно, используя признак состоятельности. Если
Mδn2® 0 при n ® ¥,
то оценка состоятельна.
Действительно, для любого e > 0
P{|dn| < e} = 1 - P{|dn| ≥ e} ≥1 -  ® 1.
® 1.
Здесь использовано обобщенное неравенство Чебышева:
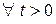 P{|x| ≥ t}
P{|x| ≥ t} 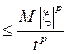 при любом p >0; здесь p = 2.
при любом p >0; здесь p = 2.
3. Оптимальность.
Критерием качества оценки j примем средний квадрат ошибки R j(a) = M[φ(ξ1, ξ2…ξn) – a ]2. Если оценка несмещённая, то критерий качества R j(a) — это дисперсия оценки.
Оценка j* называется оптимальной, если среди всех оценок j она даёт минимальное среднее значение квадрата ошибки:
 .
.
Если оценка несмещённая, то критерием качества является дисперсия.
Поскольку критерием качества оценки является не скаляр, а функция параметра, ясно, что оптимальной оценки может не существовать.
Используется и более общий подход к понятию оптимальности — критерием качества рассматривается
 ,
,
где 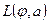 — потери (loss), которые несет статистик, если значение оценки — j, а истинное значение параметра — а.
— потери (loss), которые несет статистик, если значение оценки — j, а истинное значение параметра — а.
Например, 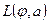 = 1, если
= 1, если 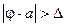 , и 0 иначе; нетрудно увидеть, что в этом случае оптимальной оценкой будет та, для которой вероятность события
, и 0 иначе; нетрудно увидеть, что в этом случае оптимальной оценкой будет та, для которой вероятность события 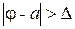 минимальна.
минимальна.
Простейшие оценки моментов
Пусть имеется выборка x1,ξ2…xn. Функция распределения F (x) наблюдений нам неизвестна.
А. оценка математического ожидания.
По определению математическое ожидание (первый момент) есть
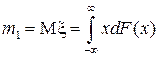 .
.
Подставим в интеграл вместо F (x) несмещенную и состоятельную оценку  (x | x1, ξ2…xn). Получим (4):
(x | x1, ξ2…xn). Получим (4):
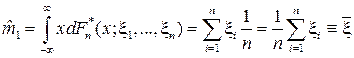
Получили (4)-дисперсию эмпирического распределения
 .
.
Рассмотрим эту статистику в качестве оценки для математического ожидания m 1. Проверим несмещённость:
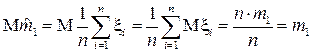 .
.
Проверим состоятельность:
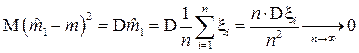 .
.
Таким образом, 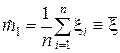 является несмещенной и состоятельной оценкой для математического ожидания.
является несмещенной и состоятельной оценкой для математического ожидания.
Заметим, что замена истинного неизвестного нам распределения эмпирическим (или выборочным) приводит к состоятельным оценкам.
Кроме того, заметим, что проверка на несмещенность и состоятельность являются стандартными действиями
Б. Оценка дисперсии.
Дисперсия случайной величины, согласно определению:
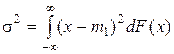 .
.
Вместо неизвестных m 1 и F (x) подставим состоятельные оценки 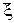 и
и 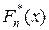 .
.
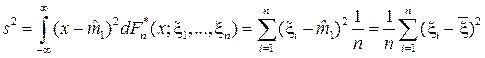
Получили оценку s 2 для s2 (формула (5) выше):
s 2 = 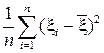 .
.
Проверим несмещённость, для чего сначала преобразуем выражение для s2:
s 2 =  =
=
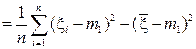 . (5а)
. (5а)
Здесь учтено, что 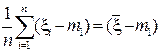 . Определим математическое ожидание:
. Определим математическое ожидание:
М s 2 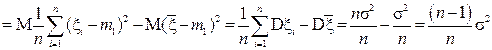 ¹s2.
¹s2.
Оно не равно s2, и потому оценка смещенная. Ясно, что ее можно исправить, умножив s 2 на константу, обратную к коэффициенту при s2. Рассмотрим исправленную оценку
s 12 =  s 2 =
s 2 = 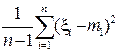 .
.
Эта оценка является несмещенной:
M s 12 =  M s 2 = s2.
M s 2 = s2.
Обе оценки s 2 и s 12 являются состоятельными, что видно из (5а), используя свойства сходимости по вероятности, аналогичные свойствам сходимости числовых последовательностей.
В. Оценка моментов порядка k > 2.
Для начального момента порядка k > 2
mk = Mx k = 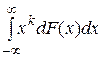 ,
,
рассмотрим оценку, полученную заменой F (x) на  (x | x1, ξ2…xn):
(x | x1, ξ2…xn):
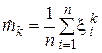 .
.
Она является несмещенной:
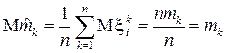 .
.
Можно показать, что оценка состоятельна, т.е.
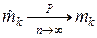 .
.
Для центрального момента порядка k > 2
m k = M(x - m1) k = 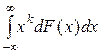 ,
,
рассмотрим оценку, полученную аналогично предыдущему:
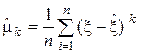 .
.
Можно показать, что данная оценка состоятельна, т.е.
 ,
,
но несмещенной она не является. И исправить ее, аналогично выборочной дисперсии, умножением на коэффициент, зависящий от n, невозможно.
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
В ТВ (в прошлом семестре) мы определяли вероятности появления различных случайных событий; закон распределения случайных факторов считали известным. В МС решается обратная задача: по наблюдаемым случайным событиям нужно сделать какие либо выводы о неизвестном законе распределения действующих случайных факторов.
Рассуждения в МС основываются на знании теории вероятностей, без уверенного знания основ которой невозможно освоить методы МС. Поэтому необходимо иметь под рукой лекции по ТВ, записи практических занятий и учебные пособия по ТВ.
----------------------------------------
Литература по МС, которая потребуется:
1. Ивченко, Медведев. Математическая статистика (есть и интернете, любое издание годится)
2. Горицкий Ю.А. Основы математической статистики. – М.: МЭИ, 2018, 84с. (есть в библиотеке МЭИ, к киоске МЭИ тоже было; лекции по этому пособию)
3. Сборник задач по математике. Теория вероятностей и математическая статистика. Под редакцией А.В. Ефимова. М.: Физматлит, 1990. (уже знакомый задачник, для решения домашних задач, есть в интернете, в библиотеке МЭИ-тоже)
4. Ю.А. Горицкий, Е.Е. Перцов. Практикум по статистике с пакетами STATGRAPHICS, STATISTICA, SPSS. М. МЭИ, 1997. 85 с.
(для лаб работ, есть в библиотеке МЭИ, кроме того, есть в интернете на Exponenta.ru)
5. Ю.А. Горицкий. Практикум по статистике с пакетом STATISTICA. М. МЭИ, 2000. 79 с. (аналогично п.4)
Все занятия будем проводить в системе Webex.
Содержание занятий
1. Лекции (1 раз в неделю)
2. Практические занятия ( по первым неделям )
3. Лаб работы (7 ЛР) ( по вторым неделям, с пакетом STATISTICA, версия 5.5а). Просьба ко всем поставить этот пакет, он бесплатный.
По каждой работе будет отмечаться: «выполнено», «отчет сделан», «защита по теме ЛР»
4. Контрольная работа «Оценки и доверительные интервалы» (9 неделя)
Зачет
Экзамен за 2 семестра
Лекция 1
ВВЕДЕНИЕ
В МС предполагается:
имеются наблюдения x º (x1, x2 … x n) случайного характера, (не обязательно числовые, могут быть, например, синий, зеленый, ….)
закон распределения частично или полностью неизвестен.
По наблюдениям нужно сделать те или иные выводы относительно неизвестного распределения.
Примеры:
1. Совокупность изделий, доля дефектных неизвестна, наудачу выбрали n штук и проверили, получили результаты: хороший (0), дефектный (1), и т. д.; неизвестная доля дефектных определяет закон распределения наших наблюдений (вероятность 0 и 1), эту долю и нужно определить.
2. Радиолокатор n раз со случайными ошибками измеряет расстояние до движущегося объекта, скорость неизвестна; по наблюдениям нужно определить скорость. Скорость определяет закон распределения измерений.
3. Новое лекарство, есть две группы испытуемых: одной дали новое, другой-старое, посмотрели результаты. Вопрос: новое лучше старого или нет? Результаты случайны, закон распределения (выздоровление или нет, определяется неизвестной вероятностью успеха)
…и.т.д.………
Задачи МС можно условно разделить на три типа:
— оценить неизвестные параметры (теория точечного оценивания);
— указать интервалы, в которых находятся неизвестные параметры (теория интервального оценивания);
— ответить на вопрос: можно ли считать, что неизвестное распределение обладает тем или иным свойством (теория проверки статистических гипотез) примеры вопросов:
- находится ли неизвестный параметр в заданном диапазоне, или нет?
- принадлежит ли неизвестный закон распределения заданному классу или нет?
- зависимы ли два признака у наблюдаемых объектов или нет? (например,форма сбственности влияет на рентабельность производства или нет? есть n наблюдений)
При рассмотрении любой статистической задачи имеющиеся наблюдения x º (x 1, x 2… x n) являются конкретными значениями многомерной случайной величины x º (x1, x2…xn). Мы должны отвлечься от конкретных значений x º (x 1, x 2… x n), нужно считать, что имеем дело со случайной вечичиной x º (x1, x2…xn) (т.е. с совокупностью возможных значений),
и потому способ обработки, который мы конструируем, должен быть «хорошим» (в некотором смысле) для всей совокупности возможных значений, а не только для имеющихся наблюдений.
Глава 1. Оценивание неизвестных параметров
Основные понятия и характеристики качества оценок
В большинстве задач математической статистики предполагается, что наблюдения (x1, x2…xn) являются независимыми, одинаково распределенными случайными величинами с функцией распределения F (x), которая является частично или полностью неизвестной. Вэтом случае они называются ВЫБОРКОЙ объема n из совокупности, распределенной по F (x). Выборка — объект случайный.
Закон распределения выборки легко определяется. Например, для непрерывного случая, если 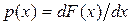 — плотность распределения одной компоненты, то плотность распределения выборки есть
— плотность распределения одной компоненты, то плотность распределения выборки есть
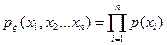 .
.
Любая функция наблюдений j(x1, ξ2…xn) (произвольной размерности) называется СТАТИСТИКОЙ. Примеры статистик:
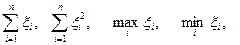
 .
.
Пусть x1, x2…xn — выборка из совокупности, распределённой по закону с функцией распределения F (x; a), зависящей от параметра а. Параметр а неизвестен, его необходимо оценить по выборке x1, ξ2…xn.
Функция наблюдений â = φ(ξ1, ξ2…ξn), с помощью которой оценивается неизвестный параметр, называется ОЦЕНКОЙ или ОЦЕНИВАЮЩЕЙ ФУНКЦИЕЙ. Заметим, что результат применения оценки â = φ(ξ1, ξ2…ξn) является случайной величиной.
Укажем те качества, которыми характеризуется оценка (оценивающая функция).
1. Несмещённость.
Оценка â = φ(ξ1, ξ2…ξn) называется несмещённой, если при любом значении параметра а
Мj = а,
где М — математическое ожидание. В противном случае оценка называется смещенной, и
Мφ – а ≡ b(а)
называется смещением.
Выпишем условие несмещённости в интегральном виде для случая непрерывного распределения:
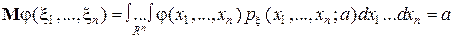 ,
,
где 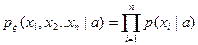 — плотность распределения выборки.
— плотность распределения выборки.
Обозначим ошибку оценки
δn = φ(ξ1, ξ2…ξn) – a.
В терминах ошибки несмещённость означает, что среднее значение ошибки равно нулю, т.е. при любом значении параметра а
Mδn = Мφ – а = 0.
2. Состоятельность.
Оценка â = φ(ξ1, ξ2…ξn) называется состоятельной, если
φ(ξ1, ξ2…ξn) ® a (по вероятности) при n ® ¥
при любом значении а.
В терминах ошибки d n состоятельность означает, что dn сходится к нулю по вероятности при любом значении а:
dn  0,
0,
т.е. для любого сколь угодно малого
e > 0 P{|dn| < e} ® 1.
Проверять состоятельность можно, используя признак состоятельности. Если
Mδn2® 0 при n ® ¥,
то оценка состоятельна.
Действительно, для любого e > 0
P{|dn| < e} = 1 - P{|dn| ≥ e} ≥1 -  ® 1.
® 1.
Здесь использовано обобщенное неравенство Чебышева:
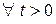 P{|x| ≥ t}
P{|x| ≥ t} 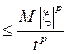 при любом p >0; здесь p = 2.
при любом p >0; здесь p = 2.
3. Оптимальность.
Критерием качества оценки j примем средний квадрат ошибки R j(a) = M[φ(ξ1, ξ2…ξn) – a ]2. Если оценка несмещённая, то критерий качества R j(a) — это дисперсия оценки.
Оценка j* называется оптимальной, если среди всех оценок j она даёт минимальное среднее значение квадрата ошибки:
 .
.
Если оценка несмещённая, то критерием качества является дисперсия.
Поскольку критерием качества оценки является не скаляр, а функция параметра, ясно, что оптимальной оценки может не существовать.
Используется и более общий подход к понятию оптимальности — критерием качества рассматривается
 ,
,
где 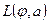 — потери (loss), которые несет статистик, если значение оценки — j, а истинное значение параметра — а.
— потери (loss), которые несет статистик, если значение оценки — j, а истинное значение параметра — а.
Например, 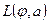 = 1, если
= 1, если 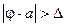 , и 0 иначе; нетрудно увидеть, что в этом случае оптимальной оценкой будет та, для которой вероятность события
, и 0 иначе; нетрудно увидеть, что в этом случае оптимальной оценкой будет та, для которой вероятность события 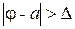 минимальна.
минимальна.



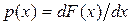 — плотность распределения одной компоненты, то плотность распределения выборки есть
— плотность распределения одной компоненты, то плотность распределения выборки есть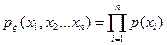 .
.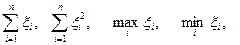
 .
.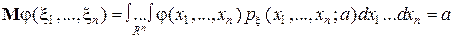 ,
,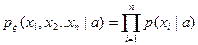 — плотность распределения выборки.
— плотность распределения выборки. 0,
0, ® 1.
® 1.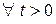 P{|x| ≥ t}
P{|x| ≥ t} 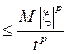 при любом p >0; здесь p = 2.
при любом p >0; здесь p = 2. .
. ,
,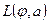 — потери (loss), которые несет статистик, если значение оценки — j, а истинное значение параметра — а.
— потери (loss), которые несет статистик, если значение оценки — j, а истинное значение параметра — а.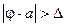 , и 0 иначе; нетрудно увидеть, что в этом случае оптимальной оценкой будет та, для которой вероятность события
, и 0 иначе; нетрудно увидеть, что в этом случае оптимальной оценкой будет та, для которой вероятность события 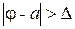 минимальна.
минимальна.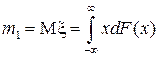 .
. (x | x1, ξ2…xn). Получим (4):
(x | x1, ξ2…xn). Получим (4):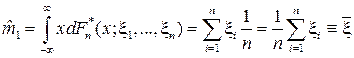
 .
.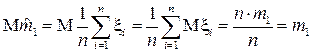 .
.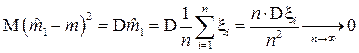 .
.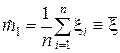 является несмещенной и состоятельной оценкой для математического ожидания.
является несмещенной и состоятельной оценкой для математического ожидания.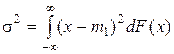 .
.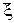 и
и 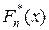 .
.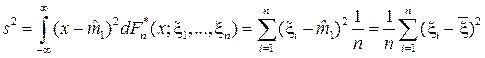
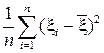 .
. =
=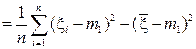 . (5а)
. (5а)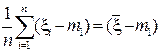 . Определим математическое ожидание:
. Определим математическое ожидание: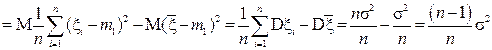 ¹s2.
¹s2. s 2 =
s 2 = 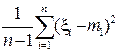 .
.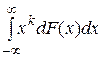 ,
,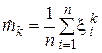 .
.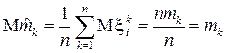 .
.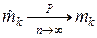 .
.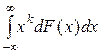 ,
,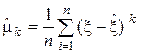 .
. ,
,

