Рассмотрим применение векторов при решении геометрических задач на примере треугольников.
Задание 1. Существует ли треугольник  , если:
, если: 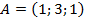 ,
, 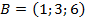 ,
, 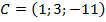 .
.
Утв. Сумма длин любых двух сторон треугольника больше длины третьей стороны.
Значит, треугольник существует, если длина большей стороны меньше суммы двух других его сторон.
Решение:
Вычислим длины сторон треугольника для этого вычислим координаты соответствующих векторов и воспользуемся формулой 7) §2:
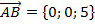 ,
, 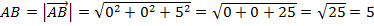 ;
;
 ,
, 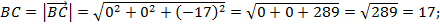
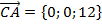 ,
,  .
.
Итак, 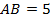 ,
, 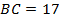 ,
, 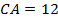 . Большая сторона
. Большая сторона 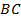 . Проверим условием существования треугольника:
. Проверим условием существования треугольника: 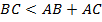 , то есть
, то есть 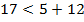 - неверно. Значит, треугольник
- неверно. Значит, треугольник  не существует.
не существует.
Ответ: не существует.
Треугольники классифицируют по 2 критериям: по стороне и по углу.
По стороне:
- равносторонний треугольник - треугольник, все 3 стороны которого равны;
- равнобедренный треугольник - треугольник, какие-либо 2 стороны которого равны;
- разносторонний треугольник - треугольник, все стороны которого различны.
По углу:
- тупоугольный треугольник - треугольник, какой либо угол которого больше  ;
;
- прямоугольный треугольник - треугольник, какой либо угол которого равен  ;
;
- остроугольный треугольник - треугольник, все углы которого меньше  .
.
Зам. Для определения вида треугольника по углу достаточно найти его больший угол. Тогда, если:
- больший угол больше  , то треугольник тупоугольный;
, то треугольник тупоугольный;
- больший угол равен  , то треугольник прямоугольный;
, то треугольник прямоугольный;
- больший угол меньше  , то треугольник остроугольный.
, то треугольник остроугольный.
Зам. Больший угол треугольника лежит против большей стороны.
Зам. При вычислении угла используют формулу 9) §2, по которой сначала вычисляется косинус данного угла, а потом определяется сам угол, значение которого может оказаться не табличным. Для определения типа треугольника по углу нахождение самого угла не требуется, достаточно определить лишь его вид. Полезно помнить, что:
- если 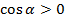 , то
, то 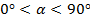 ;
;
- если  , то
, то  ;
;
- если 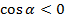 , то
, то 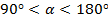 .
.
Задание 2. Определите вид треугольника  , если:
, если: 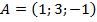 ,
, 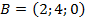 ,
,  .
.
Решение:
Вычислим длины сторон треугольника для этого составим соответствующие вектора и воспользуемся формулой 7) §2:
 ,
, 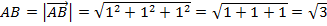 ;
;
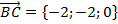 ,
, 
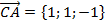 ,
,  .
.
Итак, 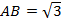 ,
,  ,
,  . Большая сторона
. Большая сторона 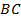 . Проверим условием существования треугольника:
. Проверим условием существования треугольника: 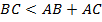 , то есть
, то есть  - верно. Значит, треугольник
- верно. Значит, треугольник  существует.
существует.
Так как 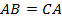 , то треугольник
, то треугольник  равнобедренный.
равнобедренный.
Большая сторона 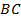 , следовательно, больший угол
, следовательно, больший угол 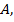 найдём его по формуле 9) §2:
найдём его по формуле 9) §2:
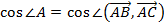 , где
, где  ,
, 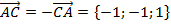

Итак, 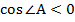 , значит угол
, значит угол 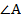 тупой и треугольник
тупой и треугольник  тупоугольный.
тупоугольный.
Ответ: треугольник  равнобедренный и тупоугольный.
равнобедренный и тупоугольный.
Задание 3. Найдите длины сторон треугольника  , длины его медиан, координаты центра и радиус описанной окружности около этого треугольника, если:
, длины его медиан, координаты центра и радиус описанной окружности около этого треугольника, если:
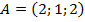 ,
, 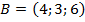 ,
, 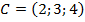 .
.
Решение:
Вычислим длины сторон треугольника для этого составим соответствующие вектора и воспользуемся формулой 7) §2:
 ,
, 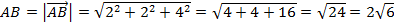 ;
;
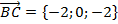 ,
, 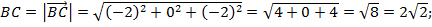

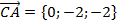 ,
, 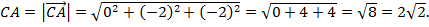
Итак,  ,
,  ,
,  . Большая сторона
. Большая сторона 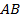 . Проверим условием существования треугольника:
. Проверим условием существования треугольника:  , то есть
, то есть 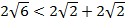 - верно. Значит, треугольник
- верно. Значит, треугольник  существует.
существует.
Так как 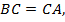 то треугольник
то треугольник  равнобедренный.
равнобедренный.
Медиана это отрезок, соединяющий вершину с серединой противоположной стороны. Пусть 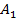 середина
середина 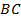 ,
, 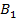 середина
середина 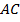 ,
,  середина
середина 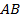 . Вычислим длины медиана
. Вычислим длины медиана  ,
, 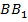 ,
,  , для этого найдем координаты точек
, для этого найдем координаты точек 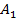 ,
, 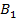 ,
,  по формуле 6) §2, составим соответствующие вектора и воспользуемся формулой 7) §2:
по формуле 6) §2, составим соответствующие вектора и воспользуемся формулой 7) §2:
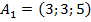 ,
, 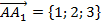 ,
, 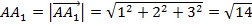 ;
;
 ,
, 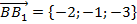 ,
, 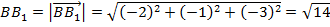 ;
;
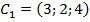 ,
,  ,
, 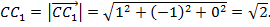
Радиус описанной около треугольника  окружности вычисляется по формуле:
окружности вычисляется по формуле:
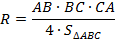
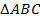 равнобедренный (
равнобедренный (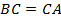 ), значит
), значит  - медиана, высота и биссектриса, поэтому
- медиана, высота и биссектриса, поэтому 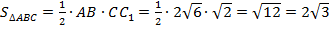 , тогда
, тогда 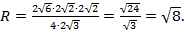
Итак, 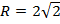 .
.
Центр описанной окружности около треугольника  совпадает с точкой
совпадает с точкой 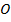 пересечения медиан. Пусть
пересечения медиан. Пусть 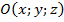 . Вычислим длины отрезков
. Вычислим длины отрезков 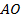 ,
,  ,
, 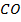 : составим соответствующие вектора и воспользуемся формулой 7) §2:
: составим соответствующие вектора и воспользуемся формулой 7) §2:
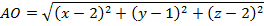
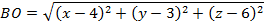

Учитывая, что 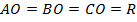 или
или  , получим
, получим
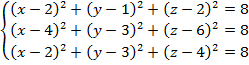
Правые части уравнений одинаковые, попарно приравняем левые (1 и 2, 1 и 3), одно (1) уравнение системы временно опустим. Получим
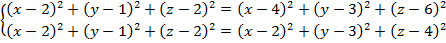 ,
,
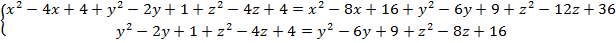 ,
,
 ,
,
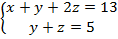 ,
,
 ,
,
 ,
,
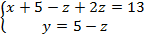 ,
,
 ,
,
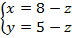 .
.
Подставим в 1 уравнение систем. Получим


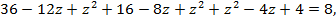
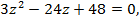

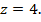
Тогда
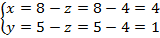 .
.
Итак,  .
.
Ответ:  ,
,  ,
,  - длины сторон треугольника;
- длины сторон треугольника;  ,
,  ,
,  - медианы треугольника; т.
- медианы треугольника; т.  ,
, 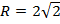 - центр и радиус описанной окружности около треугольника.
- центр и радиус описанной окружности около треугольника.



 , если:
, если: 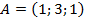 ,
, 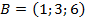 ,
, 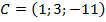 .
.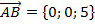 ,
, 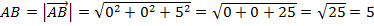 ;
; ,
, 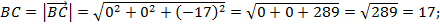
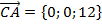 ,
,  .
.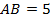 ,
, 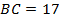 ,
, 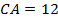 . Большая сторона
. Большая сторона 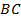 . Проверим условием существования треугольника:
. Проверим условием существования треугольника: 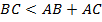 , то есть
, то есть 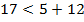 - неверно. Значит, треугольник
- неверно. Значит, треугольник  ;
;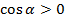 , то
, то 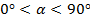 ;
; , то
, то  ;
;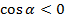 , то
, то 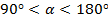 .
.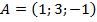 ,
, 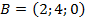 ,
,  .
. ,
, 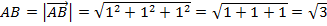 ;
;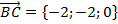 ,
, 
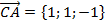 ,
,  .
.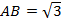 ,
,  ,
,  . Большая сторона
. Большая сторона  - верно. Значит, треугольник
- верно. Значит, треугольник 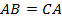 , то треугольник
, то треугольник 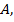 найдём его по формуле 9) §2:
найдём его по формуле 9) §2: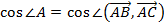 , где
, где  ,
, 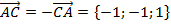

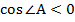 , значит угол
, значит угол 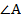 тупой и треугольник
тупой и треугольник  тупоугольный.
тупоугольный.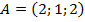 ,
, 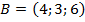 ,
, 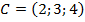 .
. ,
, 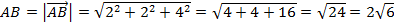 ;
;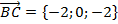 ,
, 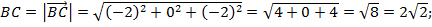

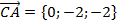 ,
, 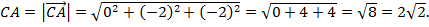
 ,
,  . Большая сторона
. Большая сторона 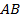 . Проверим условием существования треугольника:
. Проверим условием существования треугольника:  , то есть
, то есть 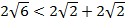 - верно. Значит, треугольник
- верно. Значит, треугольник 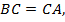 то треугольник
то треугольник  равнобедренный.
равнобедренный. середина
середина  середина
середина 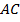 ,
,  середина
середина  ,
, 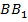 ,
,  , для этого найдем координаты точек
, для этого найдем координаты точек 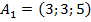 ,
, 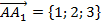 ,
, 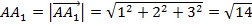 ;
; ,
, 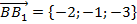 ,
, 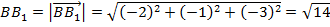 ;
;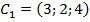 ,
,  ,
, 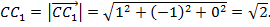
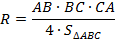
 равнобедренный (
равнобедренный ( ), значит
), значит 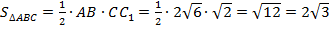 , тогда
, тогда 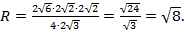
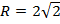 .
.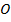 пересечения медиан. Пусть
пересечения медиан. Пусть 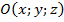 . Вычислим длины отрезков
. Вычислим длины отрезков 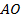 ,
,  ,
, 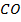 : составим соответствующие вектора и воспользуемся формулой 7) §2:
: составим соответствующие вектора и воспользуемся формулой 7) §2: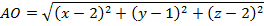
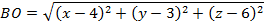

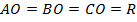 или
или  , получим
, получим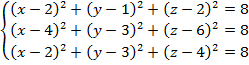
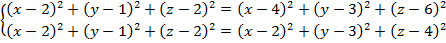 ,
,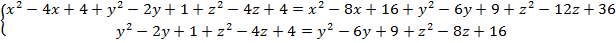 ,
, ,
,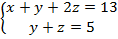 ,
, ,
,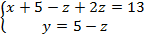 ,
, ,
,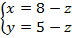 .
.

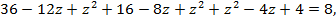
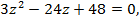

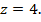
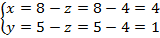 .
. .
. ,
,  ,
,  - медианы треугольника; т.
- медианы треугольника; т. 


