Рассмотрим линейную цепочку атомов, образованную рядом одинаковых рассеивающих центров а вдоль линии АВ. Пусть она рассеивает монохроматическое излучение l.
Разность хода между соседними лучами (рис. 2.8)
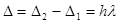 (максимум интерференции), h – целое
(максимум интерференции), h – целое
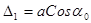
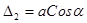
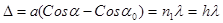 (2.12)
(2.12)
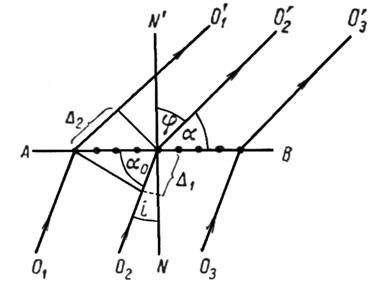
Рис. 2.8. Дифракция на линейной цепочке атомов
Постоянному значению угла a соответствуют лучи, расположенные вдоль образующих конуса с осью АВ и углом раствора 2 a.
При дифракции на линейной решетке условия максимума образуют гиперболы на плоскости(рис. 2.9).

Рис. 2.9. Возникновение светлых линий P’PP’’ при дифракции от линейной решётки
При дифракции на двумерной решетке максимумы получатся только в тех направлениях, у которых оба угла a и b одновременно удовлетворяют условиям:
 (2.13)
(2.13)
Пересечения системы двух гипербол дадут систему светлых пятен (рис.2.10).
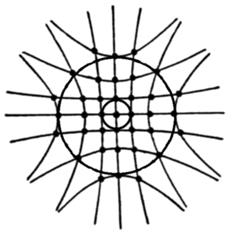
Рис. 2.10. Дифракция на двумерной и трехмерной решетках
Дифракция на трехмерной решетке (кристалл) дает максимумы при одновременном удовлетворении трех условий:
 (2.14)
(2.14)
Это три уравнения Лауэ, которые дополняются двумя геометрическими условиями:
 (2.15)
(2.15)
Уравнение Лауэ можно заменить одним интерференционным уравнением, позволяющим интерпретировать условия интерференции геометрически с помощью обратной решетки.
Обратное пространство и обратная решетка
Распространение рентгеновского излучения характеризуется длиной волны l и направлением в пространстве – углы a 0, b 0 и др.
В некоторых случаях распространение рентгеновских лучей удобнее рассматривать в  или
или  пространстве. Так как k = (2 p)/ l, т.е. обратно пропорционально длине волны, то это пространство называется обратным. В обратном пространстве вводится понятие обратной решетки, которая связана с прямой решеткой соотношениями (а *, b *, c * – параметры обратной решетки):
пространстве. Так как k = (2 p)/ l, т.е. обратно пропорционально длине волны, то это пространство называется обратным. В обратном пространстве вводится понятие обратной решетки, которая связана с прямой решеткой соотношениями (а *, b *, c * – параметры обратной решетки):
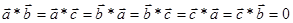 (2.16)
(2.16)
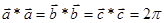
Обратное преобразование
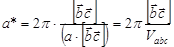
 (2.17)
(2.17)
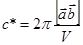
Множитель 2 p часто опускают.
При сохранении 2 p единичная трансляция в обратной решетке соответствует изменению волнового вектора на единицу: D k = ±1.
Решетка, обратная обратной решетке, есть прямая решетка.
Векторы обратной решетки 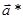 ,
, 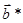 ,
, 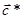 могут быть не параллельны, соответственно
могут быть не параллельны, соответственно 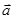 ,
, 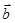 ,
,  , кроме кубической решетки. Обратная к ГЦК есть ОЦК, а к ОЦК есть ГЦК решетка.
, кроме кубической решетки. Обратная к ГЦК есть ОЦК, а к ОЦК есть ГЦК решетка.
Вектору трансляции 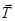 в прямой решетке
в прямой решетке
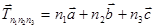 (2.18)
(2.18)
можно сопоставить трансляции в обратной решетке:
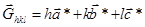 (2.19)
(2.19)
Вектор обратной решетки, задаваемый тройкой чисел h, k, l, перпендикулярен (в обратном пространстве) плоскости (hkl) в реальном пространстве. Плоскость (hkl) проходит через точки (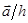 ), (
), (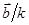 ), (
), (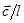 ), т.е. точке [(hkl)] в обратном пространстве соответствует плоскость (hkl) в прямом пространстве.
), т.е. точке [(hkl)] в обратном пространстве соответствует плоскость (hkl) в прямом пространстве.
В соответствии с рис. 2.11
 , (2.20)
, (2.20)
так как единичное изменение 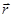 , (
, (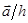 ) и dhkl соответствует 2 p.
) и dhkl соответствует 2 p.
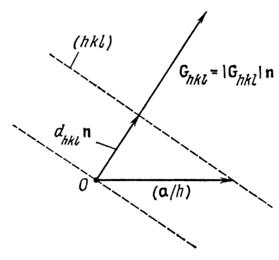
Рис. 2.11. Соотношение между прямой и обратной решетками
Выразим условие дифракции через параметры обратной решетки.
При упругом рассеянии длина вектора  не меняется, а изменяется только его направление (рис. 2.12)
не меняется, а изменяется только его направление (рис. 2.12)
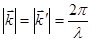 (2.21)
(2.21)
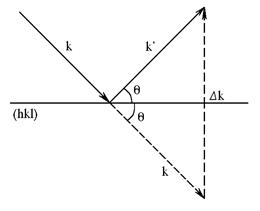
Рис. 2.12. Упругое рассеивание в обратной решетке
Вектор  перпендикулярен (hkl), т.е. совпадает с
перпендикулярен (hkl), т.е. совпадает с 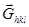 , или единичным вектором нормали
, или единичным вектором нормали  . Таким образом (рис. 2.14),
. Таким образом (рис. 2.14),

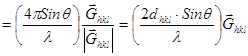 (2.22)
(2.22)
При выполнении условия Брегга 2 d × Sin q = n l получим:
 (2.23)
(2.23)
Тогда
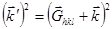 (2.24)
(2.24)
С учетом  получим условие максимума дифракции или условие Лауэ:
получим условие максимума дифракции или условие Лауэ:
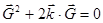 (2.25)
(2.25)
Исходя из соотношения (2.23), Эвальд в 1921 г. предложил геометрическую интерпретацию условия дифракции (2.22) с помощью сферы, построенной в обратном пространстве (рис.2.13).
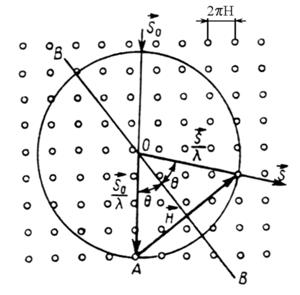
Рис. 2.13. Сфера Эвальда и условие дифракции
Сфера Эвальда образуется вектором  на узлах обратной решетки
на узлах обратной решетки  и иллюстрирует дифракцию во взаимодействии с обратной решеткой. Условие Брэгга выполняется для всех узлов обратной решетки, которые лежат на поверхности сферы. Из положения узлов обратной решетки можно вычислить прямую решетку.
и иллюстрирует дифракцию во взаимодействии с обратной решеткой. Условие Брэгга выполняется для всех узлов обратной решетки, которые лежат на поверхности сферы. Из положения узлов обратной решетки можно вычислить прямую решетку.
Практически при падении луча под одним углом для удовлетворения условия Брегга используется “белый” рентгеновский свет с длиной волны от l min до l ¥. Тогда дифракция возможна на всех узлах обратной решетки внутри сферы Эвальда с радиусом 2 p / l min.



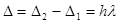 (максимум интерференции), h – целое
(максимум интерференции), h – целое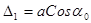
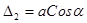
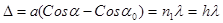 (2.12)
(2.12)

 (2.13)
(2.13)
 (2.14)
(2.14) (2.15)
(2.15) или
или  пространстве. Так как k = (2 p)/ l, т.е. обратно пропорционально длине волны, то это пространство называется обратным. В обратном пространстве вводится понятие обратной решетки, которая связана с прямой решеткой соотношениями (а *, b *, c * – параметры обратной решетки):
пространстве. Так как k = (2 p)/ l, т.е. обратно пропорционально длине волны, то это пространство называется обратным. В обратном пространстве вводится понятие обратной решетки, которая связана с прямой решеткой соотношениями (а *, b *, c * – параметры обратной решетки):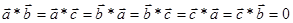 (2.16)
(2.16)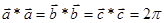
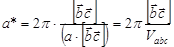
 (2.17)
(2.17)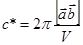
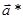 ,
, 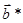 ,
, 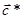 могут быть не параллельны, соответственно
могут быть не параллельны, соответственно 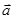 ,
, 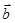 ,
,  , кроме кубической решетки. Обратная к ГЦК есть ОЦК, а к ОЦК есть ГЦК решетка.
, кроме кубической решетки. Обратная к ГЦК есть ОЦК, а к ОЦК есть ГЦК решетка.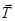 в прямой решетке
в прямой решетке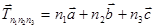 (2.18)
(2.18)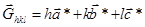 (2.19)
(2.19)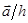 ), (
), (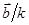 ), (
), (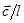 ), т.е. точке [(hkl)] в обратном пространстве соответствует плоскость (hkl) в прямом пространстве.
), т.е. точке [(hkl)] в обратном пространстве соответствует плоскость (hkl) в прямом пространстве. , (2.20)
, (2.20)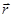 , (
, (
 не меняется, а изменяется только его направление (рис. 2.12)
не меняется, а изменяется только его направление (рис. 2.12) 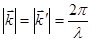 (2.21)
(2.21)
 перпендикулярен (hkl), т.е. совпадает с
перпендикулярен (hkl), т.е. совпадает с 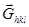 , или единичным вектором нормали
, или единичным вектором нормали  . Таким образом (рис. 2.14),
. Таким образом (рис. 2.14),
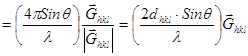 (2.22)
(2.22) (2.23)
(2.23)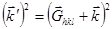 (2.24)
(2.24) получим условие максимума дифракции или условие Лауэ:
получим условие максимума дифракции или условие Лауэ: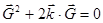 (2.25)
(2.25)
 на узлах обратной решетки
на узлах обратной решетки  и иллюстрирует дифракцию во взаимодействии с обратной решеткой. Условие Брэгга выполняется для всех узлов обратной решетки, которые лежат на поверхности сферы. Из положения узлов обратной решетки можно вычислить прямую решетку.
и иллюстрирует дифракцию во взаимодействии с обратной решеткой. Условие Брэгга выполняется для всех узлов обратной решетки, которые лежат на поверхности сферы. Из положения узлов обратной решетки можно вычислить прямую решетку.

