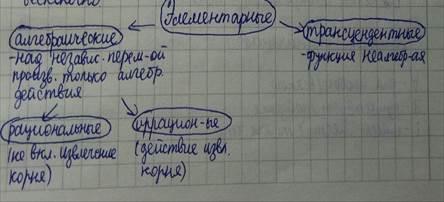
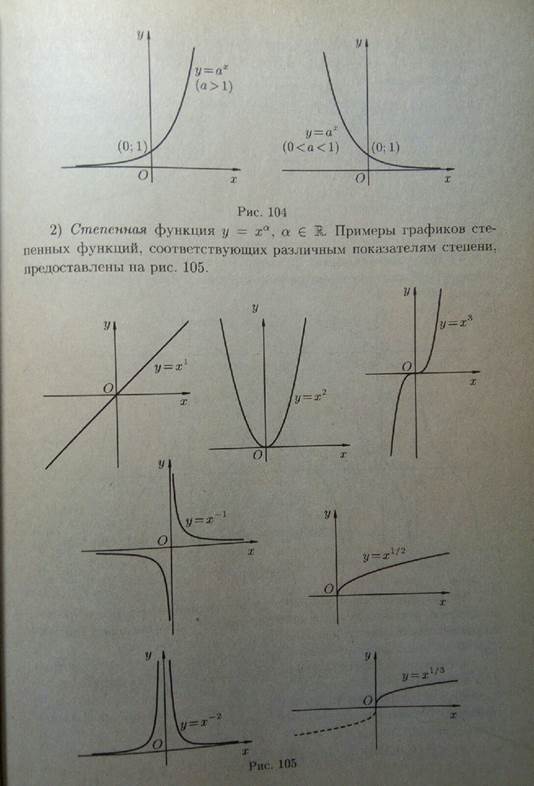
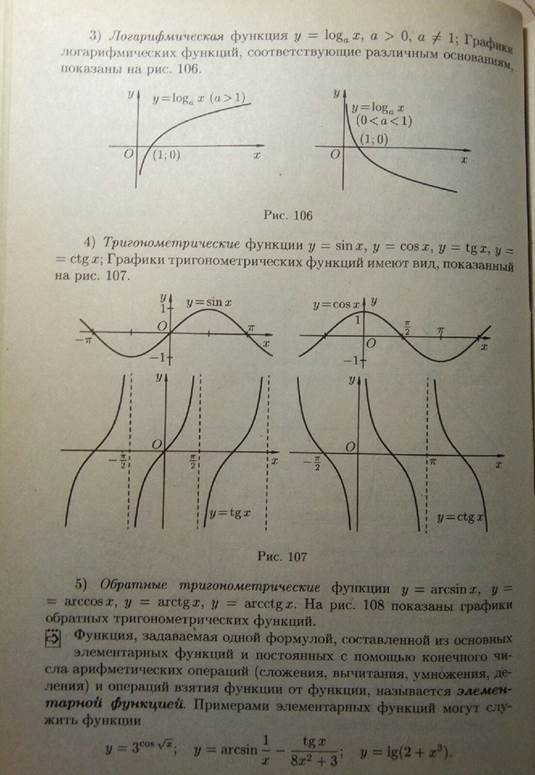
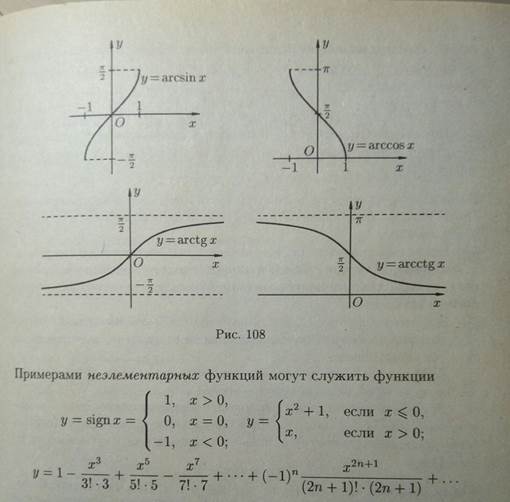
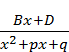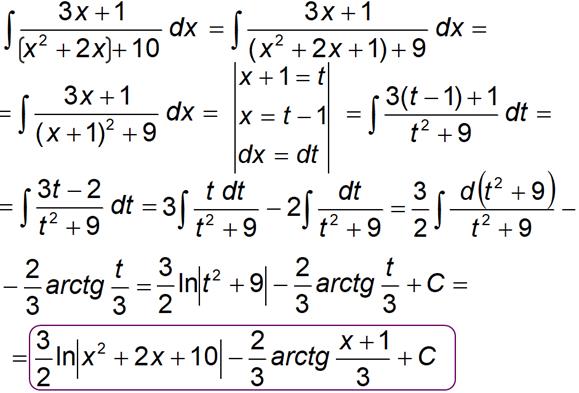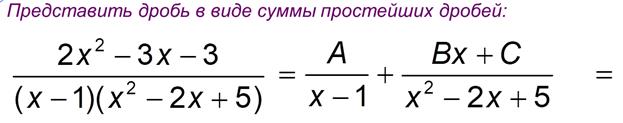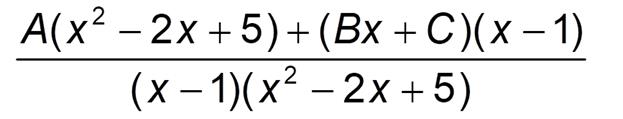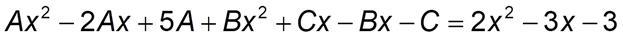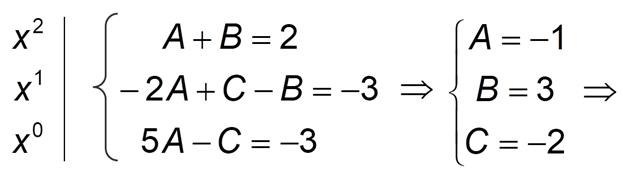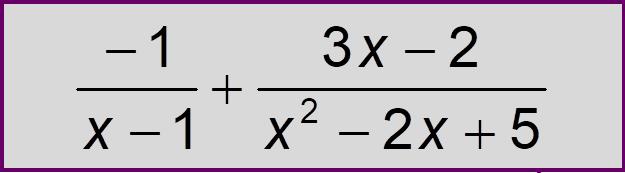Классификация функций
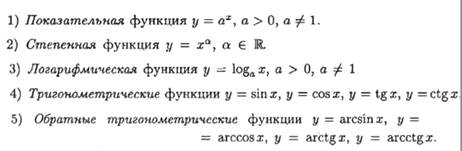




3. Основные определения, касающиеся последовательности и ее предела. Теорема о единственности предела последовательности








Теорема о единственности предела (доказательство в двух вариантах)


Необходимые и достаточные условия существования предела последовательности. Понятие о числе е


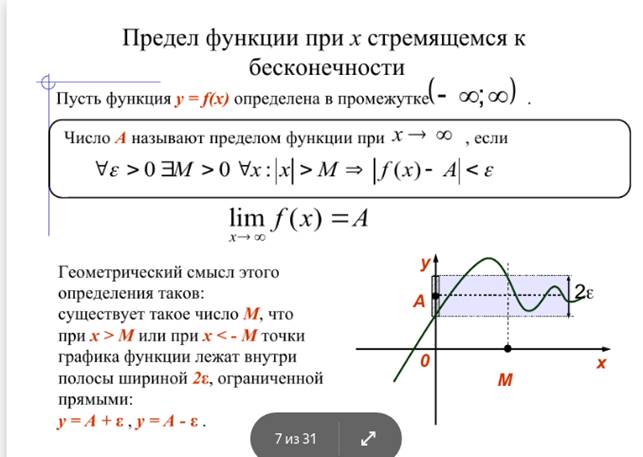
Предел функции и его геометрическая инерпретация


Понятие об односторонних пределах функции. Связь с обыкновенным пределом



Функции бесконечно малая, бесконечно большая, ограниченная и неограниченная и их свойства
Функцией называется соответствие f, которое каждому элементу xϵX сопоставляет один и только один элемент yϵY. Существуют бесконечно малые, бесконечно большие, ограниченные и неограниченные функции. (X и Y - непустые множества)
Бесконечно малые и бесконечно большие функции
Функция F(x) называется бесконечно малой в точке x0, если 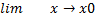 f(x) = 0. Функция F(x) называется бесконечно большой в точке х0, если
f(x) = 0. Функция F(x) называется бесконечно большой в точке х0, если 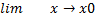 f(x) = ∞. Так Функция
f(x) = ∞. Так Функция 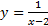 является б.б.ф. при
является б.б.ф. при 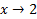 и б.м.ф. при
и б.м.ф. при 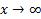 .
.
Связь б.м.ф. с б.б.ф.
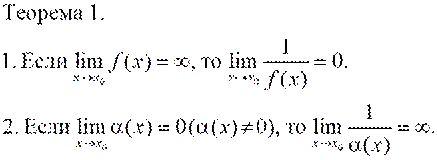
Свойства б.м.ф.



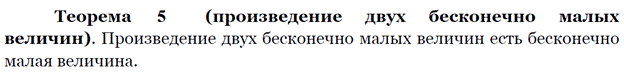

Свойства б.б.ф.(В лекциях нет)
1. С * б.б.ф. = б.б.ф. – где С- константа
2. б.б.ф. * б.б.ф. = б.б.ф.
3. б.б.ф. + б.б.ф. = б.б.ф.
Ограниченная и неограниченная функции
Обозначим буквой X некоторое множество чисел, входящих в область определения D (f) функции y = f (x).
Определение 1. Функцию y = f (x) называют ограниченной сверху на множестве X, если существует такое число a, что для любого x из множества X выполнено неравенство
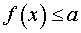
Определение 2. Функцию y = f (x) называют ограниченной снизу на множестве X, если существует такое число b, что для любого x из множества X выполнено неравенство
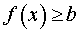
Определение 3. Функцию y = f (x) называют ограниченной на множестве X, если существуют такие числа a и b, что для любого x из множества X выполнено неравенство
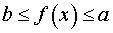
Определение 4. Функцию y = f (x) называют неограниченной сверху на множестве X, если для любого числа a существует такой x из множества X, для которого выполнено неравенство
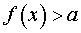
Определение 5. Функцию y = f (x) называют неограниченной снизу на множестве X, если для любого числа b существует такой x из множества X, для которого выполнено неравенство
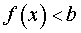
Определение 6. Функцию y = f (x) называют неограниченной на множестве X, если эта функция или неограничена сверху, или неограничена снизу, или неограничена и сверху, и снизу.
Пример 1. Функция y = x 2 (рис. 1) является ограниченной снизу и неограниченной сверху на множестве 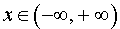
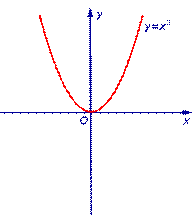
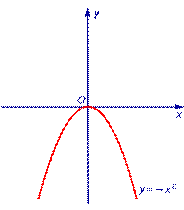
Пример 2. Функция y = – x 2 (рис. 2) является ограниченной сверху и неограниченной снизу на множестве 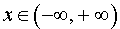
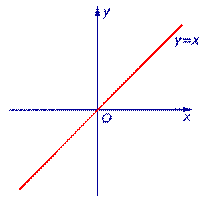
Пример 3. Функция y = x (рис. 3) неограничена сверху и неограничена снизу на множестве 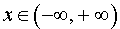
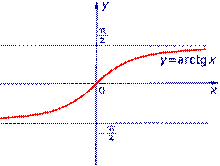
Пример 4. Функция y = arctg x (рис. 4) ограничена на множестве 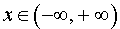
Непрерывные функции и их свойства. Классификация точек разрыва.
Непрерывность в точке

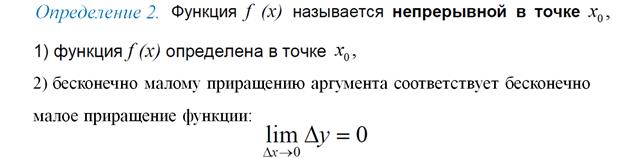






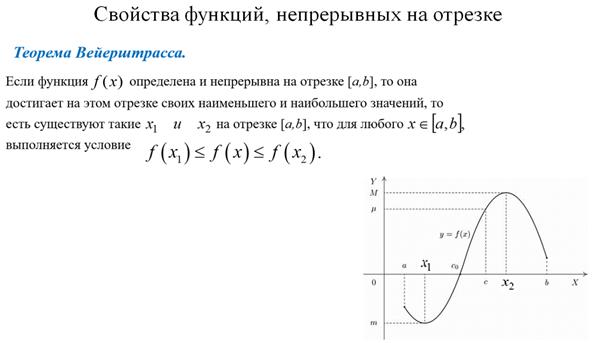
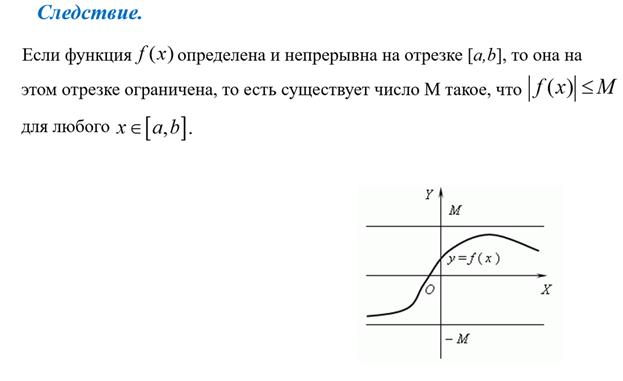
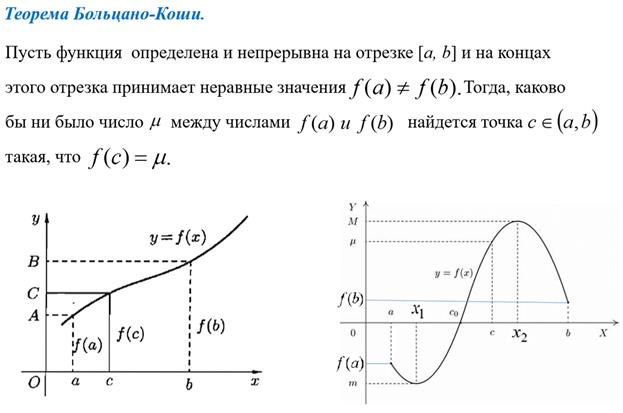
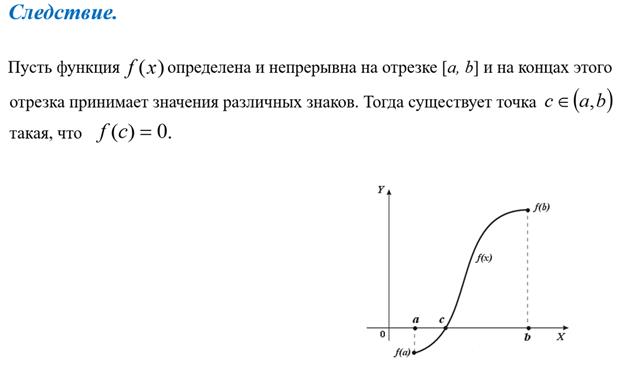


10. Первый замечательный предел и его применение

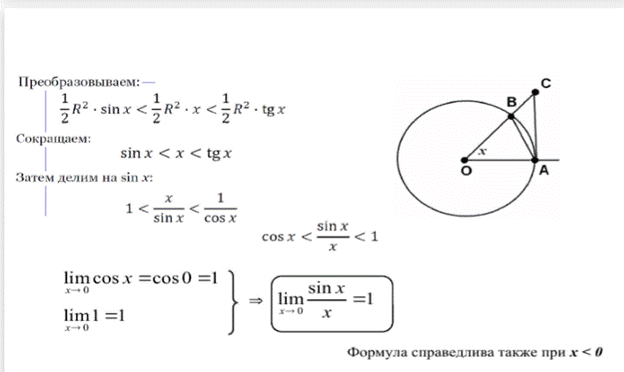

Второй замечательный предел и его основные следствия
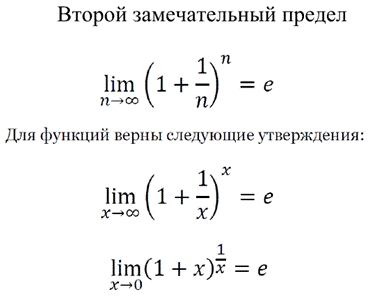
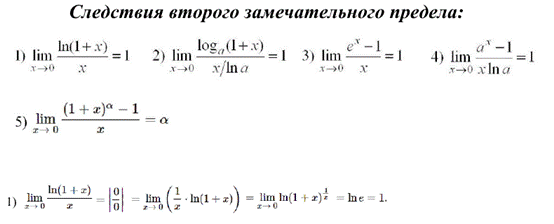
Производная сложной функции

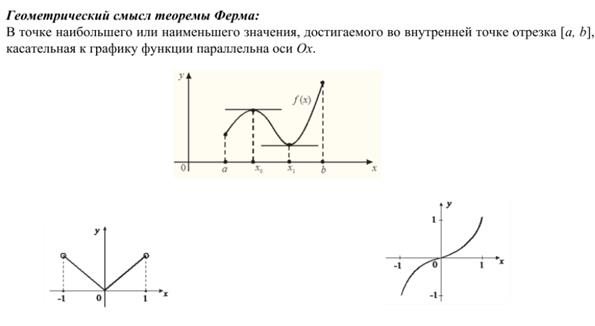
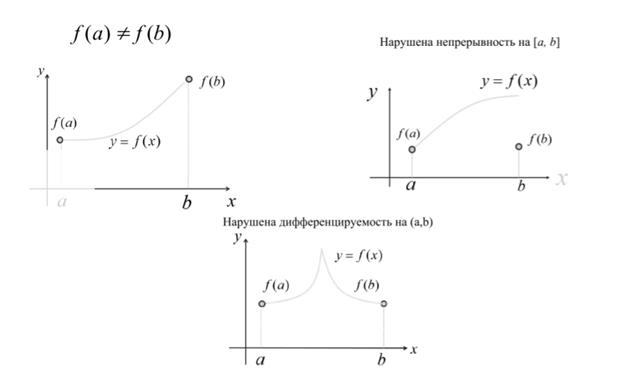
Теорема Ферма

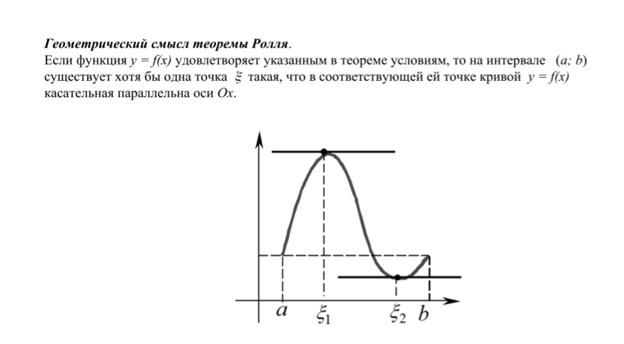
Теорема Ролля

Признак монотонности
Функция называется монотонной на промежутке, если она на этом промежутке или возрастает, или убывает.
Вертикальные асимптоты

Невертикальные асимптоты
Асимптоты бывают вертикальные, НАКЛОННЫЕ и ГОРИЗОНТАЛЬНЫЕ.
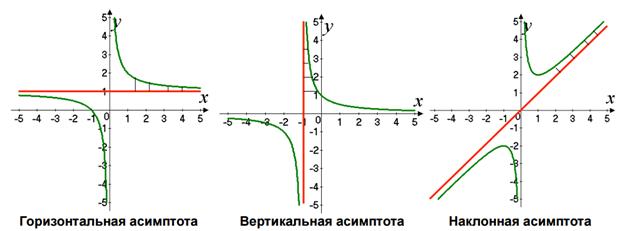
Прямая y = kx+b является наклонной асимптотой, если 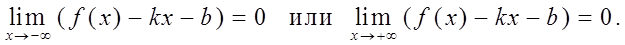
Найдём k и b.
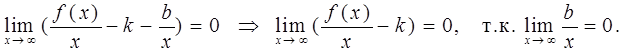
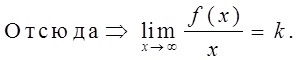 - важно.
- важно.
Итак, k и b находятся по формулам
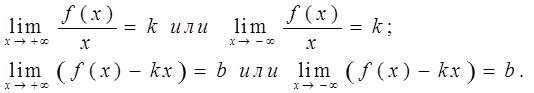
Если хотя бы один из этих пределов не существует или бесконечен, то не существует соответствующая наклонная асимптота.
У графика функции может существовать не более двух наклонных асимптот.
При k = 0 из 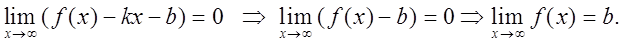
Таким образом, получаем уравнение горизонтальной асимптоты: y = b.
Теорема.
Если функция непрерывна на интервале (a, b), то она имеет на этом интервале первообразную.
Таблица основных интегралов
1. 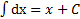 . 6.
. 6. 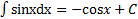 .
.
2. 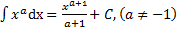 . 7.
. 7. 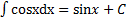 .
.
3. 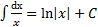 . 8.
. 8. 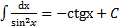 .
.
4. 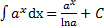 . 9.
. 9. 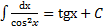 .
.
5. 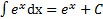 . 10.
. 10. 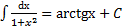 .
.
11. 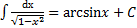
12. 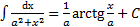
13. 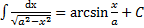
14. 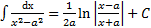
15. 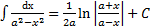
16. 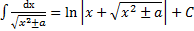
Свойства линейности неопределенного интеграла. Примеры.
№1. (Константу можно выносить за знак интеграла)

Доказательство:
1)Найдём производную левой части
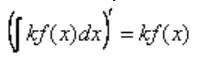
2)Найдем производную правой части
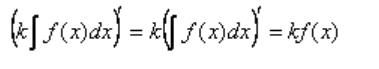
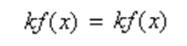
№2 (Неопределённый интеграл от алгебраической суммы функций равен алгебраической сумме интегралов)
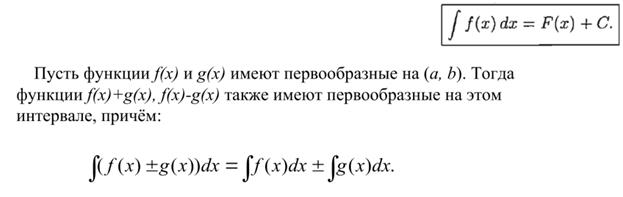
Док-во аналогично 1 (нужно продифференцировать левую и правую часть)

38) Свойства инвариантности неопределенного интеграла. Примеры.

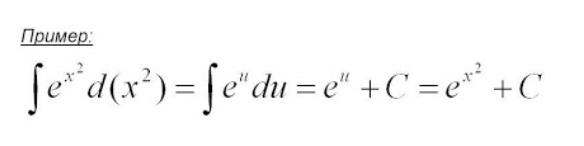
Интегрирование путем замены переменной. Примеры.

Пример:
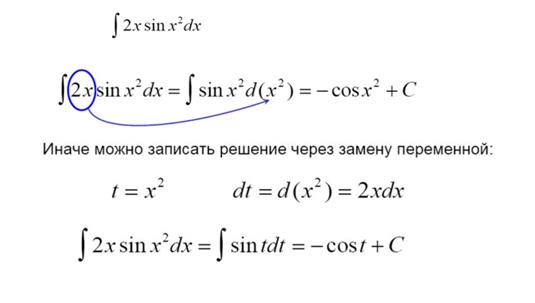
Интегрирование по частям. Примеры
Пусть u = u (x) и v = v (x) – непрерывно дифференцируемые функции.
Тогда по свойствам дифференциалов d (uv) = u ∙ dv + v ∙ du.
Проинтегрируем это равенство 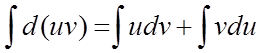
или 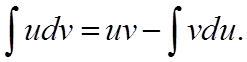
Эта формула называется формулой интегрирования по частям.
ПРИМЕР
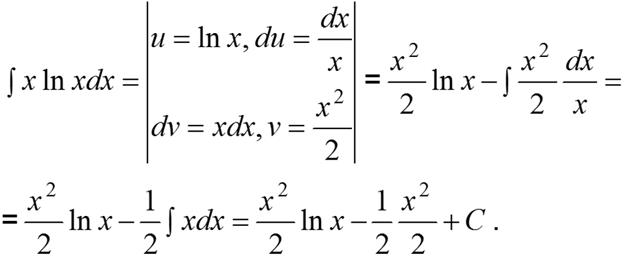
ПРИМЕР
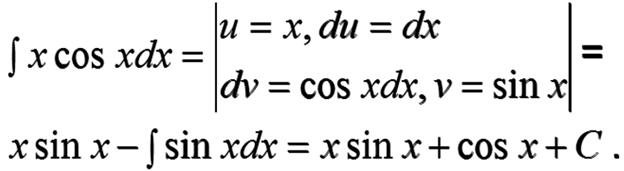
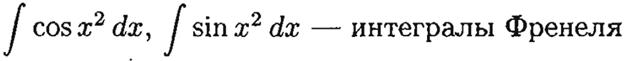
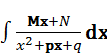 41 Интегрирование выражений вида
41 Интегрирование выражений вида 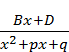
Пример 1

Пример 2
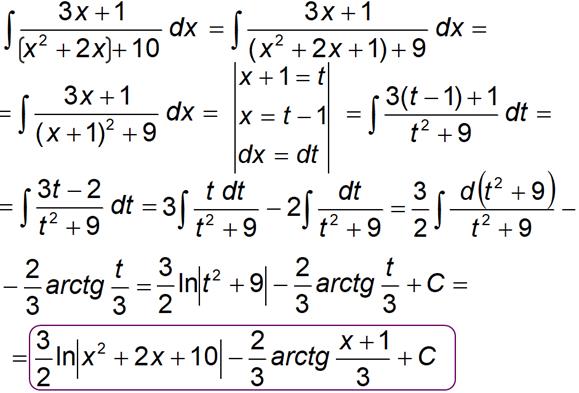
Теорема о представлении правильной алгебраической дроби в виде суммы простых дробей. Порядок действий. Пример


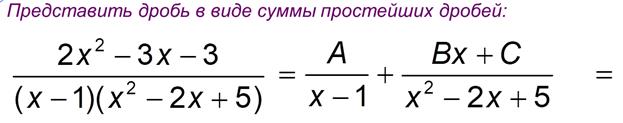
Приведем простейшие дроби к общему знаменателю
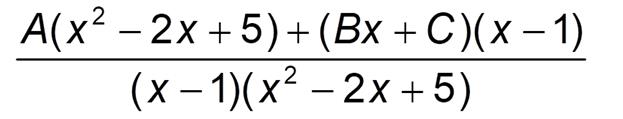
Приравняем числители получившейся и исходной дроби
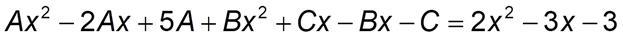
Приравняем коэффициенты при одинаковых степенях X
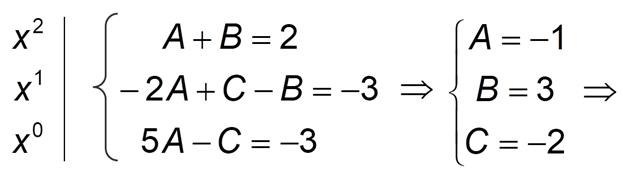
Подставляем в верхний пример (конец первой строчки)
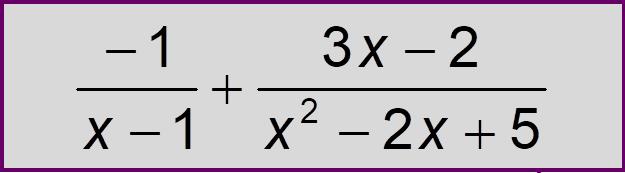
43. Алгоритм интегрирования рациональных функций
Шаг 1. Определить вид многочлена в знаменателе дроби (он может иметь действительные, кратные действительные, комплексные и кратные комплексные корни) и в зависимости от вида разложить дробь на простые дроби, в числителях которых - неопределённые коэффициенты, число которых равно степени знаменателя.
Шаг 2. Определить значения неопределённых коэффициентов. Для этого потребуется решить систему уравнений, сводящуюся к системе линейных уравнений.
Шаг 3. Найти интеграл исходной рациональной функции (дроби) как сумму интегралов полученных простых дробей, к которым применяются табличные интегралы.
Формула Ньютона-Лейбница


Классификация функций
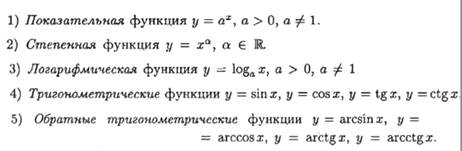








3. Основные определения, касающиеся последовательности и ее предела. Теорема о единственности предела последовательности








Теорема о единственности предела (доказательство в двух вариантах)


Необходимые и достаточные условия существования предела последовательности. Понятие о числе е





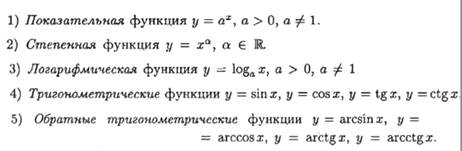


























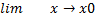 f(x) = 0. Функция F(x) называется бесконечно большой в точке х0, если
f(x) = 0. Функция F(x) называется бесконечно большой в точке х0, если 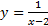 является б.б.ф. при
является б.б.ф. при 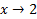 и б.м.ф. при
и б.м.ф. при 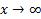 .
.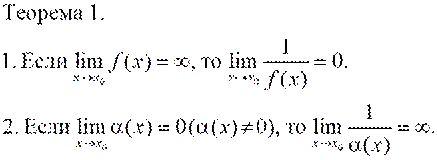



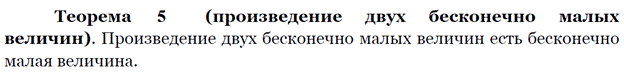

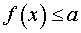
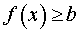
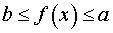
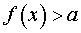
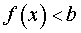
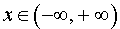





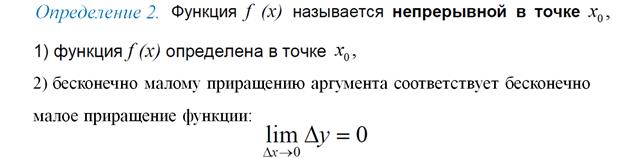















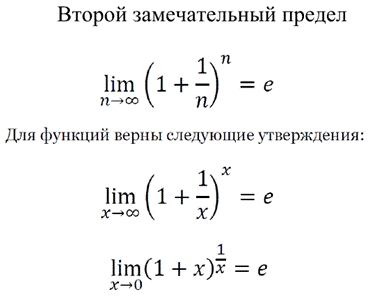
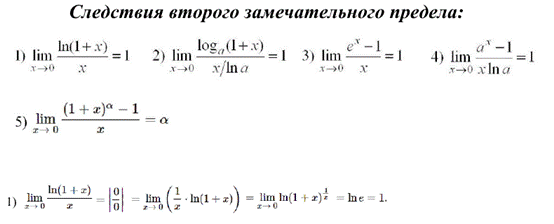








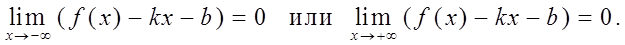
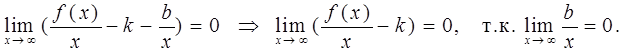
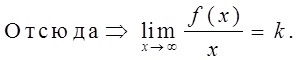 - важно.
- важно.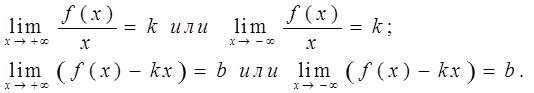
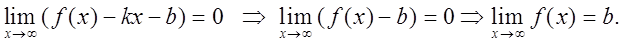
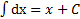 . 6.
. 6. 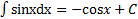 .
. 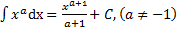 . 7.
. 7. 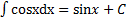 .
. 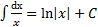 . 8.
. 8. 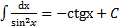 .
. 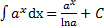 . 9.
. 9. 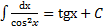 .
. 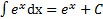 . 10.
. 10. 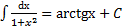 .
. 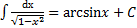
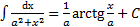
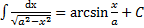
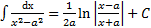
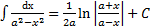
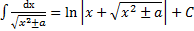

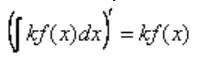
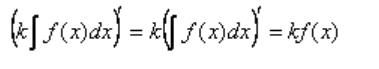
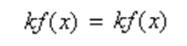
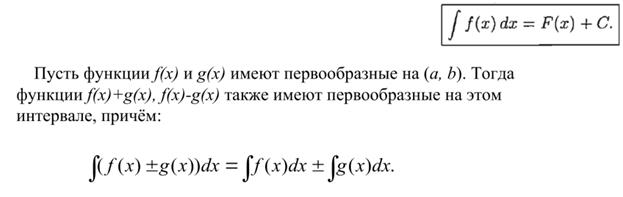


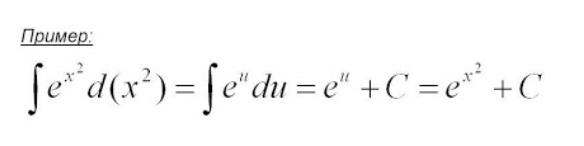

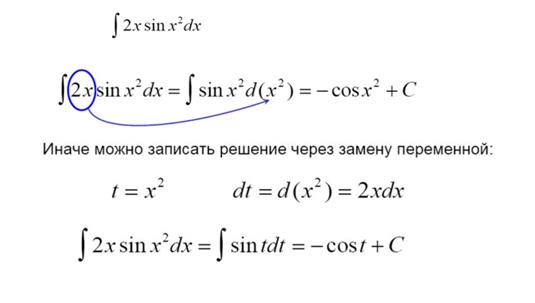
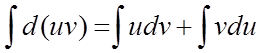
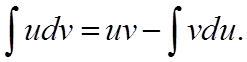
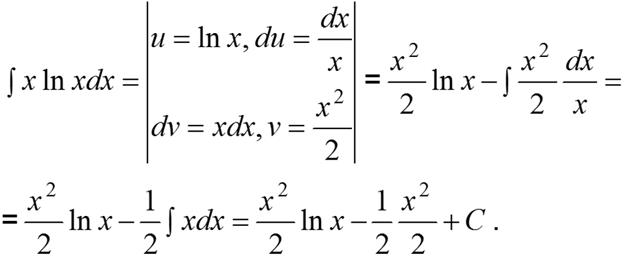
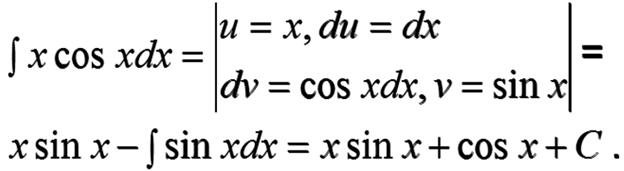
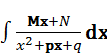 41 Интегрирование выражений вида
41 Интегрирование выражений вида