Рассмотрим метод Эйлера - линейное приближение, использующее первые два члена ряда  Тейлора. Здесь искомая интегральная кривая аппроксимируется ломаной линией. Если шаг h достаточно мал, то интеграл в формуле
Тейлора. Здесь искомая интегральная кривая аппроксимируется ломаной линией. Если шаг h достаточно мал, то интеграл в формуле  можно вычислить используя теорему о среднем, т.е. вынося подынтегральную функцию из- под знака интеграла средним значением.
можно вычислить используя теорему о среднем, т.е. вынося подынтегральную функцию из- под знака интеграла средним значением.
В методе Эйлера подынтегральная функция выносится при нижнем пределе интегрирования: 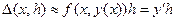 . Это приближение геометрически соответствует движению от точки x к точке х+h по касательной к кривой y(x) в точке х. Запишем расчетные формулы метода Эйлера:
. Это приближение геометрически соответствует движению от точки x к точке х+h по касательной к кривой y(x) в точке х. Запишем расчетные формулы метода Эйлера:
yk+1=yk+f(xk,yk)h, xk=xk-1+h
y(x0)=y0, yk=y(xk)
В усовершенствованном методе Эйлера- Коши в первом приближении полагается:
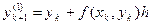
а во втором 
Погрешность метода Эйлера определяется остаточным членом ряда Тейлора


т.е. R~h2 на каждом шаге вычислений. Для обеспечения сходимости шаг h следует выбирать достаточно малым. Для метода Эйлера- Коши погрешность имеет порядок h2.
Рассмотрим метод Рунге и Кутта. В основе получения вычислительных схем этого метода лежит разложение функции y(x) в ряд Тейлора с последующим преобразованием отрезка ряда к виду, не содержащему производных. На шаге h производная dy/dx=f(x,y) аппроксимируется параболой второго порядка. Здесь функция D(x,h) определяется формулой парабол Симпсона (формула Ньютона - Котеса для трех узлов):
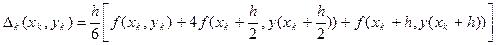
Рассмотрим дифференциальное уравнение 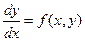 при начальном условии (хА,уА). Выполним следующие операции:
при начальном условии (хА,уА). Выполним следующие операции:
1) По известным начальным условиям (хА,уА) определим значение производной в начальной точке А: 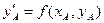 .
.
Из начальной точки А проведем прямую 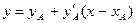 (рис 1.2.)
(рис 1.2.)
и отметим значение ее ординаты в середине шага интегрирования h (точка В с координатами
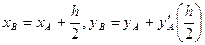 ).
).
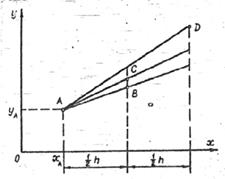
Рис 1.2.
2) Найдем значение производной по формуле 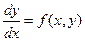 в точке В:
в точке В:  и проведем из точки А прямую
и проведем из точки А прямую 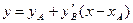 . Отметим значение ординаты этой прямой в середине шага интегрирования h (точка С с координатами
. Отметим значение ординаты этой прямой в середине шага интегрирования h (точка С с координатами  ).
).
3) По уравнению 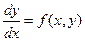 найдем значение производной в точке С:
найдем значение производной в точке С: 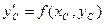 и проведем из точки А прямую
и проведем из точки А прямую 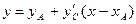 . Отметим значение ординаты этой прямой в конце шага интегрирования h (точка D с координатами
. Отметим значение ординаты этой прямой в конце шага интегрирования h (точка D с координатами 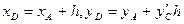 ).
).
4) По уравнению 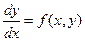 найдем значение производной в точке D:
найдем значение производной в точке D:  .
.
В результате построений найдем значение производных  в точках А, В,С и D. Отложим эти значения на графике рис 1.3. Как видно из графика, в точке с абсциссой
в точках А, В,С и D. Отложим эти значения на графике рис 1.3. Как видно из графика, в точке с абсциссой  получены два значения производной вместо одного. Это следствие приближенности метода. Примем в этой точке среднее значение производной:
получены два значения производной вместо одного. Это следствие приближенности метода. Примем в этой точке среднее значение производной:  . Отложив на графике (рис 1.3.) ординату
. Отложив на графике (рис 1.3.) ординату  , получим точку М.
, получим точку М.

Рис 1.3.
Будем считать, что кривая, изображающая зависимость  должна проходить через точки A,M и D. Проведем через эти три точки параболу, уравнение которой:
должна проходить через точки A,M и D. Проведем через эти три точки параболу, уравнение которой:
 .
.
Значения коэффициентов a,b и с выбираются из условия прохождения параболы через точки А, М, и D. Коэффициент 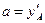 . Из уравнения параболы
. Из уравнения параболы  имеем систему:
имеем систему:
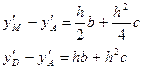
Решив эти уравнения, найдем:
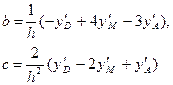
Проинтегрируем теперь уравнение параболы  в пределах от x=xA до x=xA+h. Значение этого интеграла является приращением искомой функции y при изменении х на величину h. Таким образом
в пределах от x=xA до x=xA+h. Значение этого интеграла является приращением искомой функции y при изменении х на величину h. Таким образом  Подставив сюда полученные выше выражения для a,b,c, после приведения подобных членов для общего случая (
Подставив сюда полученные выше выражения для a,b,c, после приведения подобных членов для общего случая (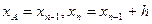 ) получим:
) получим:
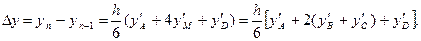
Как видно, приращение искомой функции на шаге h при помощи описанных построений удалось представить через значения первых производных функции в четырех точках, лежащих в пределах шага интегрирования h.
Запишем расчетные формулы метода Рунге- Кутта:
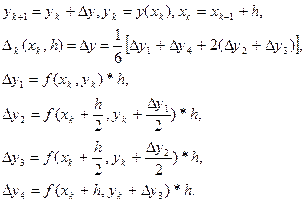
При условии существования у функции  производных четвертого порядка погрешность метода является величиной порядка h5.
производных четвертого порядка погрешность метода является величиной порядка h5.
Для системы дифференциальных уравнений первого порядка данный алгоритм выполняется для каждого уравнения системы параллельно.



 Тейлора. Здесь искомая интегральная кривая аппроксимируется ломаной линией. Если шаг h достаточно мал, то интеграл в формуле
Тейлора. Здесь искомая интегральная кривая аппроксимируется ломаной линией. Если шаг h достаточно мал, то интеграл в формуле  можно вычислить используя теорему о среднем, т.е. вынося подынтегральную функцию из- под знака интеграла средним значением.
можно вычислить используя теорему о среднем, т.е. вынося подынтегральную функцию из- под знака интеграла средним значением.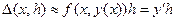 . Это приближение геометрически соответствует движению от точки x к точке х+h по касательной к кривой y(x) в точке х. Запишем расчетные формулы метода Эйлера:
. Это приближение геометрически соответствует движению от точки x к точке х+h по касательной к кривой y(x) в точке х. Запишем расчетные формулы метода Эйлера: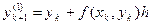


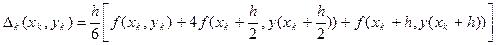
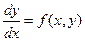 при начальном условии (хА,уА). Выполним следующие операции:
при начальном условии (хА,уА). Выполним следующие операции: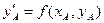 .
.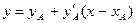 (рис 1.2.)
(рис 1.2.)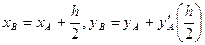 ).
).
 и проведем из точки А прямую
и проведем из точки А прямую 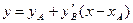 . Отметим значение ординаты этой прямой в середине шага интегрирования h (точка С с координатами
. Отметим значение ординаты этой прямой в середине шага интегрирования h (точка С с координатами  ).
).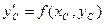 и проведем из точки А прямую
и проведем из точки А прямую 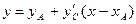 . Отметим значение ординаты этой прямой в конце шага интегрирования h (точка D с координатами
. Отметим значение ординаты этой прямой в конце шага интегрирования h (точка D с координатами 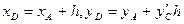 ).
). .
. в точках А, В,С и D. Отложим эти значения на графике рис 1.3. Как видно из графика, в точке с абсциссой
в точках А, В,С и D. Отложим эти значения на графике рис 1.3. Как видно из графика, в точке с абсциссой  получены два значения производной вместо одного. Это следствие приближенности метода. Примем в этой точке среднее значение производной:
получены два значения производной вместо одного. Это следствие приближенности метода. Примем в этой точке среднее значение производной:  . Отложив на графике (рис 1.3.) ординату
. Отложив на графике (рис 1.3.) ординату  , получим точку М.
, получим точку М.
 должна проходить через точки A,M и D. Проведем через эти три точки параболу, уравнение которой:
должна проходить через точки A,M и D. Проведем через эти три точки параболу, уравнение которой: .
.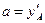 . Из уравнения параболы
. Из уравнения параболы 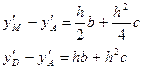
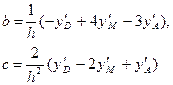
 Подставив сюда полученные выше выражения для a,b,c, после приведения подобных членов для общего случая (
Подставив сюда полученные выше выражения для a,b,c, после приведения подобных членов для общего случая (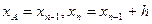 ) получим:
) получим: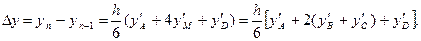
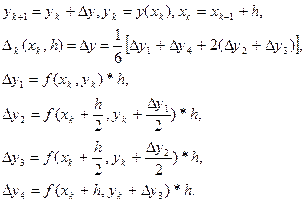
 производных четвертого порядка погрешность метода является величиной порядка h5.
производных четвертого порядка погрешность метода является величиной порядка h5.


