Перевозок.
Очень часто на практике при решение Т.З либо какой-то производитель или потребитель закладывает “запрет“ на продукцию.
Если это производитель – то он может запретить перевозку своего товара любому потребителю своей продукции.
Если это потребитель – то он может запретить перевозку товара к себе любому производителю с которым нехочет иметь дело.
В этом случае клетка с номером i, j должна быть заблокирована. И осуществляется это следующим образом. В клетку с номером i, j место Cij записываем число m (очень большое положительное число).
Задачи о назначении.
Пусть имеются m исполнителей которые должны быть назначены на выполнение n работ.
Известна матрица C. С – затраты при назначении i – исполнителя на выполнение j – вида работ C = Cij
Произвести назначение таким образом, чтобы каждый исполнитель выполнял только 1 работу, и каждая работа выполнялась только 1 исполнителем. При этом затраты должны быть минимальными.
Возможные постановки:
Ai – Экономисты. (i = 1,m) Bj – Работа. (j = 1,n) Cij – Затраты.
Ai – Строительные механизмы. Bj –Площади. Cij – производительность.
Математическая модель.
Предположим m=n. Введем целочисленное обозначение пусть Xij 1- i-ый на j—ю, 0 в противном случае. Получим матрицу из элементов 0 и 1. Так как исполнитель может быть назначен на одну работу и одна работа может быть выполнена только одним исполнителем в каждой строке и столбце только одна 1. Система ограничение все = 1 (по строкам и столбцам) Х –(0;1) Z=двойная сумма СijXij ->min =>Задача о назначениях является частной Т.З., где ai и bj=1 причем r=m+n-1=2n-1>n –решение всегда выраждена.
Теоремы на которых основаны решения задачи о Назначениях.
Т. Кенинга Если элементы матрицы С, разделить на два класса, на основании свойства R, то минимальное число линий содержащих все элементы со свойством R = максимальному числу таких элементов со свойством R, не какие два из которых не лежат на одной прямой.
Теорема: Решения задачи о назначениях не изменится если к матрице прибавить или отнять из каждого столбца иил каждой строки одно и тоже число.
С=¦Сij¦
C1=¦Cij-Ui+Vj¦ - док-ть что Х не изменится.
Z1(X)= 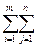 (Cij-Ui+Vj)Xij=
(Cij-Ui+Vj)Xij= 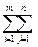 CijXij-
CijXij-  UiXij+
UiXij+ 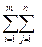 VjXij=Z(x)-
VjXij=Z(x)- 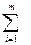 Ui
Ui  Xij +
Xij +  Vj
Vj 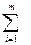 Xij = > Z1(x)=Z(x)-
Xij = > Z1(x)=Z(x)- 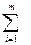 Ui+
Ui+  Vj – очевидно что решение не изменилось
Vj – очевидно что решение не изменилось  Xij=1
Xij=1
Изменилось только значение функции
3) Если можно найти такую матрицу назначений функции Х, для которой значение функции Z будет равно=0 то Х является оптимальным решением данной задачи. Если Xij>=0; Сij>=0, то произведение их Сij*Xij>=0 сумма их тоже >=0. Очевидно что самое минимальное число 0, Х – будет являться решением задачи. => назначение производится по 0.
Алгоритм решения.
1. Все действия выполняются с матрицей С
2. Из каждой строки матрицы вычитается минимальный элемент этой строки
3. Так же и столбец
4. Минимальным числом линий вычеркиваем все 0, если число линий = n то произодим назначение.
5. Если число линий меньше n, то выбираем минимальный элемент из не вычеркнутых и вычитаем его из не вычеркнутых, а перечеркнутым дважды прибавляем.
Задача коммивояжера.
Постановка задачи:
Известно что комиваяжер выезжает из города и должен посетить A1, A2, A3,…, AK городов и вернутся в город A1. Известно расстояние Cij между городами Ai – Bj причем известно Cij ¹ Cji.
Cij = Cjj = ¥. Спланировать маршрут таким образом, чтобы расстояние L для этого маршрута (I1, I2 , I3,…, Ik) было кротчайшим.
Математическая модель этой задачи:
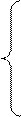
х11+х12+…+х1k =1
x21+x22+…+x2k =1
xk1+xk2+…+xkk = 1
x11+ +x21 +xk1 = 1
x12+ x22+ xk2 = 1
x1k+ x2k+ +xkk = 1
Z = 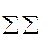 CijXij ® min
CijXij ® min
Маршрут – это цикл.
Метод ветвей и границ.
1. Допустимые множества в задачи коммивояжера
F(x) ® min (1,2,3,…,K,1)
XÎД (1,3,2,…,K,1)
Для задачи допустимым планом является маршрут от 1 города, 2, 3. О.Д.Р. – есть множество маршрутов (перестановки).
2. Нижняя оценка (граница).

Д
Нижней оценкой к x где Д* множество – называется такое число x* = d(Д*) удовлетворяет условию x* £ f(x) где XÎД*.
Ветвлениею
Ветвление на множестве Д такое разбиение множества Д на k ³ 2 подмножеств. Дi (i =1,k) для которых справедливы следующие 2 условия.
1. Пересечение 2 подмножеств Дi1 Ç Дi2 = Æ есть пустое множество, а
2. Обьединение всех подмножеств È Дi = Д
В результате ветвей получим дерево решений.
Вершина от которой нет ответвлений называется висячей вершиной. Если выходит две стрелки, то дерево называется диадическое дерево
Перспективное ветвление.
Пусть на каком то шаге дерево возможных вариантов, каждый из которых имеет нижнюю оценку, на очередном шаге выбирается для ветвления вершина с наименьшей минимальной оценкой. и та вершина становится перспективной.
Признак оптимальности.
F(x)=min оценки Д (последней) Пусть есть матрица Х* принадлеж Дк, такой что f(x*)= сигма (Дк) => Х* оптимальное решение.



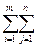 (Cij-Ui+Vj)Xij=
(Cij-Ui+Vj)Xij= 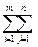 CijXij-
CijXij-  UiXij+
UiXij+ 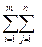 VjXij=Z(x)-
VjXij=Z(x)- 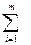 Ui
Ui  Xij +
Xij + 
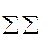 CijXij ® min
CijXij ® min 




