Типовые задачи, используемые при формировании

вариантов текущего контроля

Домашнее задание №1  (часть 1) «Линейные и евклидовы пространства»

Задача 1.       Исследуйте на линейную зависимость систему векторов ,                                  , .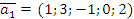

Задача 2.       Рассматривая векторы 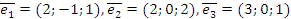 как новый базис в 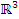, вычислите

а) координаты вектора 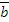 в исходном базисе, зная его координаты в новом базисе ;

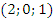б) координаты вектора 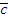 в новом базисе, зная его координаты в исходном базисе .

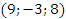Задача 3.       Даны координаты векторов в некотором ортонормированном базисе:

, , .

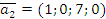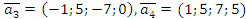Применяя процесс ортогонализации, ортонормируйте эту систему векторов.

Домашнее задание №1 (часть 2) «Линейные операторы и квадратичные формы»

Задача 4. Найдите собственные значения и собственные векторы линейного оператора, заданного в некотором базисе матрицей .

Задача 5. Приведите матрицу  к диагональному виду и укажите матрицу перехода.

 Задача 6. Приведите квадратичную форму 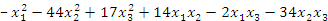 к каноническому виду методом Лагранжа.

Задача 7. Приведите квадратичную форму  к каноническому виду ортогональным преобразованием.

 

Задача 8. Уравнение (а) кривой  второго порядка на плоскости Oxy и уравнение (б) поверхности второго порядка в пространстве Oxyz приведите к каноническому виду, указав:

1) одно из преобразований перехода от заданной прямоугольной декартовой системы координат к канонической системе координат (собственные числа матрицы квадратичной формы расположите в порядке возрастания),

2) канонический вид уравнения кривой (а) и поверхности (б), значения всех параметров, характеризующих кривую и поверхность,

3) на плоскости Oxy постройте каноническую систему координат, кривую (а) и найдите в системе Oxy для центральной кривой координаты центра, вершин, фокусов, уравнения асимптот (для гиперболы), а для параболы – координаты вершины, фокуса, уравнения директрисы,

4) в канонической системе координат постройте поверхность (б), используя метод сечений.

      

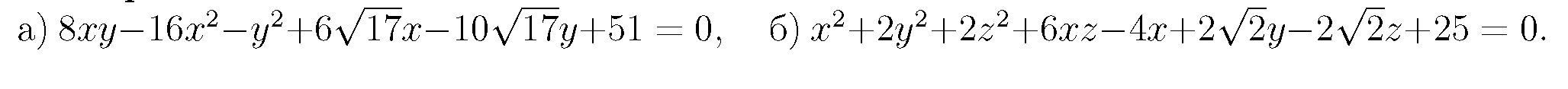
Домашнее задание №2 «Функции нескольких переменных»

Задача 1. Для заданной функции выполните следующие задания.

1. Найдите и изобразите на пл. ХОУ область определения (границы, принадлежащие области определения, стройте сплошной чертой, не принадлежащие - пунктиром.)

2. Составьте уравнения линий уровня и изобразите в области определения. Выделите уравнение той из них, которая проходит через заданную точку , изобразите её (другим цветом) на общем рисунке.

3. В заданной точке М вычислите производную функции по направлению вектора 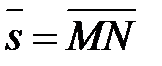, где 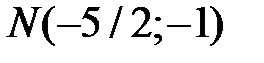. Найдите вектор градиента, постройте его на общем рисунке.

4. Вычислите наибольшее значение производной функции по направлению в точке М и укажите, в каком направлении 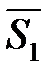она достигается.

Задача 2. Найдите первый дифференциал:

а) для функции ;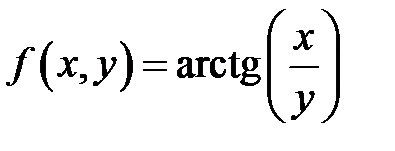

б) для сложной функции ;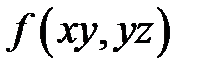

в) для неявной функции ;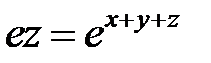

г) для неявной функции .

В пункте а) найдите второй дифференциал.

Задача 3. Убедитесь, что выражение    является полным дифференциалом некоторой функции, найдите эту функцию.

Задача 4. Покажите, что заданная функция   удовлетворяет уравнению .

Задача 5. На поверхности, заданной уравнением 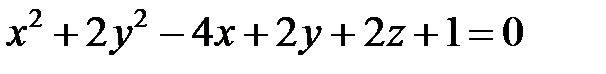найдите точки, в которых касательная плоскость к поверхности перпендикулярна заданному вектору . Составьте уравнения касательной плоскости и нормали к поверхности, проходящие через найденные точки.

Задача 6. Исследуйте функцию 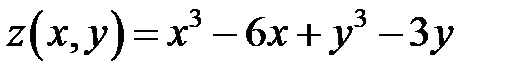 на локальные экстремумы.

 

  Контрольная работа

Задача 1. Для  функции 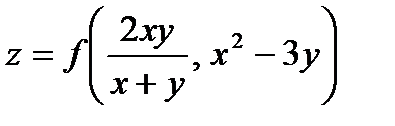найдите .

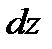Задача 2. Вычислите  для функции , заданной неявно уравнением .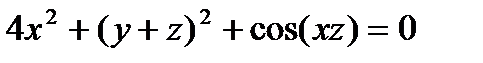

Задача 3. Для функции 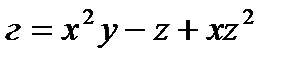 и точке  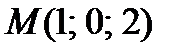найдите наибольшее значение производной по направлению.

Задача 4. Составьте уравнения касательной плоскости и нормали к поверхности 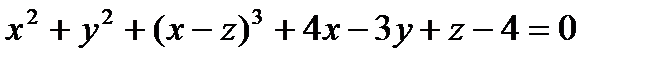 в точке .

 

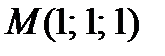Контроль по модулю №1

Задача 1. Дайте определение линейного пространства и докажите следствия из аксиом.

Задача 2. Приведение матрицы самосопряженного оператора к диагональному виду ортогональным преобразованием. Приведите пример.

Задача 3. Докажите, что оператор поворота на угол 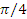 вокруг оси  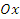в 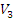 является линейным. Выпишите матрицу этого оператора и найдите образ вектора 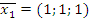. Ответ проверьте геометрически.

Задача 4. Исследуйте знакоопределенность квадратичной формы  в зависимости от значения параметра .

Задача 5. Докажите, что векторы 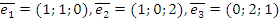 образуют базис в  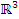и найдите координаты вектора  в этом базисе.

Задача 6.    Квадратичная форма в некотором ортонормированном базисе имеет вид . Найдите ортогональное преобразование, приводящее квадратичную форму к каноническому виду. Напишите этот канонический вид.

Контроль по модулю №2

Задача 1. Дайте определение предела ФНП и сформулируйте его свойства. Бесконечно малые и бесконечно большие ФНП

Задача 2. Дайте определение точки локального экстремума ФНП. Выведите необходимые условия экстремума ФНП. Сформулируйте достаточные условия.

 Задача 3. В точке М (2; 1; 1;) найдите градиент и производную по направлению  функции 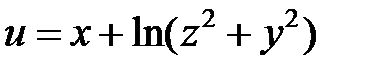, если N (0; 2; -1), а также максимальное значение производной по направлению в точке M.

Задача 4. Найдите  и  для функции 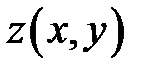, заданной уравнением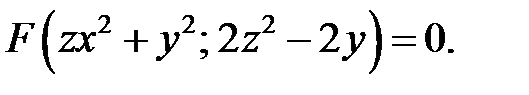

 Задача 5. Найдите условные экстремумы функции 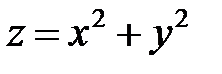 при условии .

 

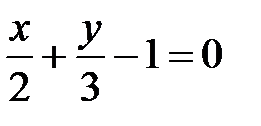Вопросы для подготовки к контролям по модулям

Модуль 1 Линейная алгебра

1. Дайте определение линейного пространства, сформулируйте следствия из его аксиом и приведите примеры.

2. Дайте определение линейно зависимой и линейно независимой систем векторов линейного пространства. Сформулируйте критерий линейной зависимости. Свойства линейно зависимых и линейно независимых систем векторов.

3. Дайте определение базиса и размерности линейного пространства. Связь между этими понятиями. Приведите примеры. Сформулируйте теорему о единственности разложения по базису вектора линейного пространства. Линейные операции с векторами в координатной форме.

4. Дайте определение подпространства линейного пространства. Приведите пример. Дайте определение линейной оболочки системы векторов и сформулируйте её основное свойство.

5. Дайте определение ранга системы векторов линейного пространства. Сформулируйте теорему о ранге системы векторов и её следствие.

6. Линейное преобразование линейного пространства (переход к новому базису). Матрица перехода. Изменение координат вектора при переходе к новому базису (вывод).

7. Дайте определение евклидова пространства. Приведите примеры. Напишите формулы для вычисления скалярного произведения двух векторов и нормы вектора в ортонормированном базисе.

8. Дайте определение ортонормированной системы векторов евклидова пространства и докажите ее линейную независимость.

9. Процесс ортогонализации Грама-Шмидта в евклидовом пространстве (без док-ва). Приведите пример.

10. Дайте определение нормы вектора в евклидовом пространстве. Неравенство Коши-Буняковского и неравенство треугольника (с выводом).

11. Дайте определение линейного оператора и действий с линейными операторами.

Матрица линейного оператора, определение и примеры. Сформулируйте теоремы о связи между действиями с линейными операторами и действиями с соответствующими им матрицами.

12. Докажите теорему о связи между матрицами одного и того же линейного оператора в различных базисах. Инвариантность определителя. Подобные матрицы.

13. Дайте определение собственных значений и собственных векторов линейного оператора. Приведите примеры. Докажите инвариантность характеристического многочлена и спектра собственных значений линейного оператора относительно выбора базиса.

14. Докажите теорему о линейной независимости собственных векторов линейного оператора, соответствующих попарно различным собственным значениям.

15. Докажите теорему о матрице линейного оператора в базисе из собственных векторов.

16.  Дайте определение оператора, сопряженного данному линейному оператору, и сформулируйте его свойства. Теорема о матрице сопряженного оператора в ортонормированном базисе (без док-ва).

17. Дайте определение самосопряженного линейного оператора, докажите теорему о симметричности его матрицы в ортонормированном базисе. Теорема о корнях характеристического уравнения самосопряженного линейного оператора и ее следствия (формулировки). Случай кратных корней (формулировка).

18. Докажите теорему об ортогональности собственных векторов самосопряженного линейного оператора, соответствующих различным собственным значениям.

19. Дайте определение ортогональной матрицы. Сформулируйте ее свойства.

20. Ортогональные преобразования и их матрицы в ортонормированном базисе. Примеры. Приведение матрицы самосопряженного линейного оператора к диагональному виду ортогональным преобразованием.

21. Дайте определение симметричной билинейной формы и ее матрицы. Координатная, матричная и векторная форма записи этой формы. Сформулируйте теорему о её матрице.

22. Дайте определение квадратичной формы и докажите теорему о связи между матрицами одной и той же квадратичной (билинейной) формы в различных базисах.

23. Дайте определение ранга квадратичной формы. Сформулируйте закон инерции квадратичных форм.

24. Дайте определение канонического вида и канонического базиса квадратичной формы. Сформулируйте теорему о возможности приведения квадратичной формы к каноническому виду.

25. Метод Лагранжа приведения квадратичной формы к каноническому виду. Приведите пример.

26. Приведение квадратичной формы к каноническому виду ортогональным преобразованием. Приведите пример.

27. Знакоопределенные квадратичные формы: определение, критерий Сильвестра (без док-ва). Приведите примеры.

28. Приведение линий и поверхностей второго порядка к каноническому виду.

Вопросы с доказательством, включенные в контроль по модулю № 1

 

1.Переход к новому базису линейного пространства. Изменение координат вектора при переходе к новому базису.

2.Норма вектора. Неравенства Коши-Буняковского и треугольника.

3.Теорема о связи между матрицами одного и того же линейного оператора в различных базисах линейного пространства.

4.Теорема о линейной независимости ортогональной системы векторов евклидова пространства.

5.Теорема об инвариантности характеристического многочлена линейного оператора относительно замены базиса.

6. Теорема о линейной независимости собственных векторов линейного оператора, соответствующих попарно различным собственным значениям.

7.Теорема о матрице линейного оператора в базисе из собственных векторов.

8.Теорема о матрице самосопряженного линейного оператора в ортонормированном базисе.

9.Теорема об ортогональности собственных векторов самосопряженного линейного оператора, соответствующих различным собственным значениям.

10.Теорема о связи между матрицами одной и той же билинейной (квадратичной) формы в различных базисах.