Последовательности
Определение 1. Числовой последовательностью ( в дальнейшем просто последовательностью) называется упорядоченное счетное множество чисел
{ x 1, x 2, x 3,... }.
Обратите внимание на два момента.
1. В последовательности бесконечно много чисел. Если чисел конечное число – это не последовательность!
2. Все числа упорядочены, то есть расположены в определенном порядке.
В дальнейшем для последовательности часто будем использовать сокращенное обозначение { xn }.
Над последовательностями можно производить определенные операции. Рассмотрим некоторые из них.
Определение. Если каждому числу n натурального ряда чисел 1, 2,..., n,... ставится в соответствие по определенному закону некоторое вещественное число xn, то множество вещественных чисел x1, x2, x3,..., xn мы назовем числовой последовательностью или просто последовательностью. Сокращенно последовательность обозначается - {xn}.
]Задание последовательностей
Чтобы понять смысл слов: „по определенному закону“ ниже на примерах показано, как могут задаваться последовательности ("законы" выделены жирным шрифтом):
1, 2, 3, 4, 5, 6,..., n,... - последовательность натуральных чисел.
2, 4, 6, 8, 10,..., 2n,... - последовательность чётных чисел.
1, 3, 5, 7, 9,..., 2n+1,... - последовательность нечётных чисел.
3,14; 3,141; 3,1415; 3,14159;...; 3,1415926535897932384626433832;...; 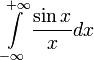 ;... - последовательность приближённых значений числа π с увеличивающейся точностью.
;... - последовательность приближённых значений числа π с увеличивающейся точностью.
В общем виде последовательности задаются в виде функции, являясь результатом их вычисления.
Связь с функцией
Определение. Числовая последовательность — функция от одного натурального аргумента.
xn - члены числовой последовательности. n - номер члена числовой последовательности. { xn } или 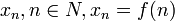 - общий член.
- общий член.
Таким образом, числовая последовательность это частный вид функции, в котором элементу из множества натуральных чисел по определенному закону однозначно ставится в соответствие элемент из множества вещественных чисел.
1. Умножение последовательности на число.
Последовательность c ×{ xn } – это последовательность с элементами { c × xn }, то есть
c × { x 1, x 2, x 3,... }={ c × x 1, c × x 2, c × x 3,... }.
2. Сложение и вычитание последовательностей.
{ xn }±{ yn }={ xn ± yn },
или, более подробно,
{ x 1, x 2, x 3,... }±{ y 1, y 2, y 3,... }={ x 1± y 1, x 2± y 2, x 3± y 3,... }.
3. Умножение последовательностей.
{ xn }×{ yn }={ xn × yn }.
4. Деление последовательностей.
{ xn }/{ yn }={ xn / yn }.
Естественно, предполагается, что в этом случае все yn ¹0.
Определение 2.
Последовательность { xn } называется ограниченной сверху, если 

 .
.
Последовательность { xn } называется ограниченной снизу, если 

 .
.
Последовательность { xn } называется ограниченной, если она одновременно ограничена и сверху и снизу.
Предел последовательности.
Основное определение. Число a называется пределом последовательности { xn } при n стремящимся к бесконечности, если
 .
.
Для этого факта используют следующие обозначения:
 или
или 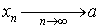 .
.
Подчеркнем, что N зависит от e.
Варианты определения.
Говорят, что 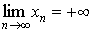 , если
, если  .
.
Говорят, что  , если
, если  .
.
Последовательность { xn } называется бесконечно большой, если 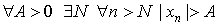 (то есть, если
(то есть, если  ).
).
Теорема.
Если последовательность { xn } сходится и ее предел равен a, то любая ее подпоследовательность также сходится и имеет тот же самый предел.
Если { xn } – бесконечно большая последовательность, то любая ее подпоследовательность есть также бесконечно большая.
Последовательности
Определение 1. Числовой последовательностью ( в дальнейшем просто последовательностью) называется упорядоченное счетное множество чисел
{ x 1, x 2, x 3,... }.
Обратите внимание на два момента.
1. В последовательности бесконечно много чисел. Если чисел конечное число – это не последовательность!
2. Все числа упорядочены, то есть расположены в определенном порядке.
В дальнейшем для последовательности часто будем использовать сокращенное обозначение { xn }.
Над последовательностями можно производить определенные операции. Рассмотрим некоторые из них.
Определение. Если каждому числу n натурального ряда чисел 1, 2,..., n,... ставится в соответствие по определенному закону некоторое вещественное число xn, то множество вещественных чисел x1, x2, x3,..., xn мы назовем числовой последовательностью или просто последовательностью. Сокращенно последовательность обозначается - {xn}.
]Задание последовательностей
Чтобы понять смысл слов: „по определенному закону“ ниже на примерах показано, как могут задаваться последовательности ("законы" выделены жирным шрифтом):
1, 2, 3, 4, 5, 6,..., n,... - последовательность натуральных чисел.
2, 4, 6, 8, 10,..., 2n,... - последовательность чётных чисел.
1, 3, 5, 7, 9,..., 2n+1,... - последовательность нечётных чисел.
3,14; 3,141; 3,1415; 3,14159;...; 3,1415926535897932384626433832;...; 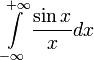 ;... - последовательность приближённых значений числа π с увеличивающейся точностью.
;... - последовательность приближённых значений числа π с увеличивающейся точностью.
В общем виде последовательности задаются в виде функции, являясь результатом их вычисления.
Связь с функцией
Определение. Числовая последовательность — функция от одного натурального аргумента.
xn - члены числовой последовательности. n - номер члена числовой последовательности. { xn } или 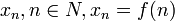 - общий член.
- общий член.
Таким образом, числовая последовательность это частный вид функции, в котором элементу из множества натуральных чисел по определенному закону однозначно ставится в соответствие элемент из множества вещественных чисел.
1. Умножение последовательности на число.
Последовательность c ×{ xn } – это последовательность с элементами { c × xn }, то есть
c × { x 1, x 2, x 3,... }={ c × x 1, c × x 2, c × x 3,... }.
2. Сложение и вычитание последовательностей.
{ xn }±{ yn }={ xn ± yn },
или, более подробно,
{ x 1, x 2, x 3,... }±{ y 1, y 2, y 3,... }={ x 1± y 1, x 2± y 2, x 3± y 3,... }.
3. Умножение последовательностей.
{ xn }×{ yn }={ xn × yn }.
4. Деление последовательностей.
{ xn }/{ yn }={ xn / yn }.
Естественно, предполагается, что в этом случае все yn ¹0.
Определение 2.
Последовательность { xn } называется ограниченной сверху, если 

 .
.
Последовательность { xn } называется ограниченной снизу, если 

 .
.
Последовательность { xn } называется ограниченной, если она одновременно ограничена и сверху и снизу.
Предел последовательности.
Основное определение. Число a называется пределом последовательности { xn } при n стремящимся к бесконечности, если
 .
.
Для этого факта используют следующие обозначения:
 или
или 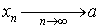 .
.
Подчеркнем, что N зависит от e.
Варианты определения.
Говорят, что 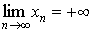 , если
, если  .
.
Говорят, что  , если
, если  .
.
Последовательность { xn } называется бесконечно большой, если 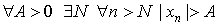 (то есть, если
(то есть, если  ).
).
Бесконечно малые последовательности.
Оределение. Последовательность { xn } называется бесконечно малой, если  , то есть если
, то есть если  .
.
Бесконечно малые последовательности имеют следующие свойства.
1. Сумма и разность бесконечно малых последовательностей есть также бесконечно малая последовательность.
2. Бесконечно малая последовательность ограничена.
3. Произведение бесконечно малой последовательности на ограниченную последовательность есть бесконечно малая последовательность.
4. Если { xn } – бесконечно большая последовательность, то, начиная с некоторого N, определена последовательность {1/ xn }, и она есть бесконечно малая последовательность. Наоборот, если { xn } – бесконечно малая последовательность и все xn отличны от нуля, то {1/ xn } есть бесконечно большая последовательность.



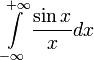 ;... - последовательность приближённых значений числа π с увеличивающейся точностью.
;... - последовательность приближённых значений числа π с увеличивающейся точностью.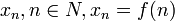 - общий член.
- общий член.

 .
.
 .
. .
. или
или 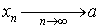 .
.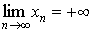 , если
, если  .
. , если
, если  .
.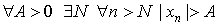 (то есть, если
(то есть, если  ).
). , то есть если
, то есть если  .
.


