Постановка задачи динамического программирования

Реферат

По математическим основам теории систем

На тему

Динамическое программирование и вариационное исчисление

 

Выполнил:

Группа: ПС-263

Проверил: Разнополов О. А.

 

Челябинск

2003

Динамические задачи оптимизации управления

Многошаговые процессы управления

Оптимальное управление как вариационная задача

Постановка вариационной задачи

 

Обычно задачи, требующие минимизации функционала, подчиненного дифференциальному соот­ношению, при наличии интегрального ограничения заменяются минимизацией нового функционала

J(u)= 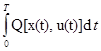+ λ ,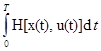

подчиненного только дифференциальному соотношению. Параметр λ, в функционале, получивший название множителя Лагранжа, в задачах оптимизации управления играет роль «цены» ограниченных ресурсов. Его значение находится из граничных условий вариационной задачи.

Возможность упрощения вариационной задачи с интегральными ограничениями посредством введения множителей Лагранжа вытекает из следующей теоремы.

Теорема 1. Если u(t)-оптимальное управление, при котором функционал J(u)= 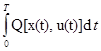+λ 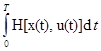достигает абсолютного минимума и выполняется ограничение 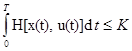, тогда при u(t) достигается абсолютный минимум функционала J(u)= 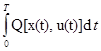, подчиненного ограничению .

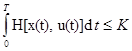Доказательство: следует от противного. Пусть v(t)-другое управление, отличное от u(t), причем такое, что <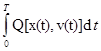

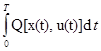
и выполнено условие .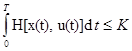

Тогда 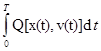+λ ≤ +λ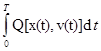K< +λK=

= +λ , что противоречит предположению, что u(t) обращает J(u)= 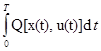+λ 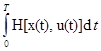в минимум.

Важнейшим понятием вариационного исчисления является понятие вариации функции, которое при исследовании функционалов играет такую же роль, как дифференциал при исследовании функций.

Пусть f(x) – функция, непрерывная на интервале [a,b]. Рассмотрим внутреннюю точку х этого интервала и некоторое фиксированное значение дифференциала аргумента функции ∆x=dx. Разность f(x+∆x)-f(x)=df(x)=f(x)∆x называется дифференциалом функции f(x) в точке х. Как известно, условие df(x)=0 является необходимым условием минимума (максимума) функции f(x) в точ­ке х.

Получим аналогичные соотношения в вариационноми исчислении.

Рассмотрим задачу с закреплёнными концами при фиксированном времени.

Пусть задана некоторая целевая функция

J= 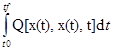à min, при условиях x(t0)=x0, x(tf)=xf, t 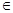[t0,tf], x(t) 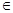Rn, причём x(t) непрерывна, и дифференцируема.

Пусть у нас имеется оптимальное решение x(t)=x*(t).

Проведём сдвиг от этого решения: выберем произвольную функцию η(t), такую, что η(t0)=η(tf)=0, η(t) 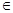Rn,причём η(t) непрерывна, и дифференцируема.

Метод динамического программирования

Реферат

По математическим основам теории систем

На тему

Динамическое программирование и вариационное исчисление

 

Выполнил:

Группа: ПС-263

Проверил: Разнополов О. А.

 

Челябинск

2003

Динамические задачи оптимизации управления

Постановка задачи динамического программирования

Среди разнообразных задач кибернетики значительное место занимают задачи, в которых объект управления находится в состоянии непрерывного движения и изменения под воздействием различных внешних и внутренних факторов. Задачи управления такими объектами относятся к классу динамических задач управления.

Объект называется управляемым, если среди действующих на него разнообразных факторов имеются такие, распоряжаясь которыми, можно изменять характер его движения. Такие целенаправленные воздействия называются управлениями и обозначаются u(t).

Характер движения объекта управления определяется системой дифференциальных уравнений, которую удобно сокращенно записывать в векторной форме в виде одного дифференциального уравнения:

x(t)=g(x,u), x(0)=c.

Управление u(t) входит в уравнение, так что это уравнение определяет не просто конкретное движение объекта, а лишь его технические возможности, которые могут быть реализованы путем использования того или иного управления из пространства допустимых управлений U.

Оценить, насколько при том или ином способе управления достигаются поставленные цели, можно, как и раньше, путем введения целевой функции, которую в данном случае удобно записать в виде

J=J[x(t),x(t),u(t),t].

Так, если u(t) - мгновенный расход топлива, а x(t) - мгновенная скорость самолета, то с точки зрения расхода топлива качество управления в любой момент времени может быть охарактеризовано величиной J(t)=u(t)/x(t) (мгновенный расход топлива на едини­цу пути), которая, естественно, будет зависеть от состояния природы, т.е. от совокупности внешних факторов, определяющих условия полета.

Целевая функция в виде, записанном выше, используется редко, так как она дает оценку лишь мгновенных значений управляемого процесса, тогда как в большинстве задач бывает необходимо оценить процессы в объекте управления на протяжении всего времени управления от 0 до Т.

Во многих случаях целевую функцию удается подобрать так, что оценку процесса в объекте управления можно произвести путем интегрирования целевой функции за все время управления, т.е. за критерий качества управления принять функционал J(u)= .

Так, если целевая функция имеет физический смысл потерь, то можно определяет суммарные потери за весь процесс управления.

Иногда в качестве цели управления удается задать желаемый ход процесса z(t). При этом в качестве целевой функции можно взять квадрат или абсолютное значение отклонения процесса x(t) от желаемого:

J=[x(t)-z(t)]2, J=| x(t)-z(t)|.

В этих случаях критерий качества управления будет определять полную квадратичную или абсолютную ошибку.

В динамических задачах управления наряду с ограничениями, определяющими пространство допусхидшх. управлений U, приходится иметь дело с интегральными ограничениями вида

.

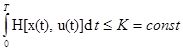Весьма часто, например, приходится сталкиваться с необходимостью ограничения пределов изменения мгновенного значения некоторого параметра а(х,u) в процессе управления. Обозначим через a0 то значение параметра а, превышение которого является нежелательным. Если подынтегральную функцию H(х, u), называемую в данном случае функцией штрафа, определить из соотношения

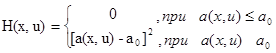
то интегральное ограничение будет выражать требование, чтобы мгновенное параметра а могло превышать а0 лишь кратковременно и на незначительную величину. Это условие будет выполняться тем жестче, чем меньше К. так, при К=0 ограничение вообще не будет допускать превышениен а над а0.

Такие ограничения возникают также тогда, когда приходится иметь дело с ограниченными ресурсами: может быть ограничено находящееся в распоряже­нии количество энергии, топлива,если речь идет о траекториях, и т.п.

Приведенные соотношения позволяют дать следующее определение оптимального управления в динамических системах. Оптимальным называется управление u*(t), выбираемое из прастранства допустимых управлений U, такое, которое для объекта, описываемого дифференциальным уравнением, минимизирует критерий качества при заданных ограничениях на используемые ресурсы.