Частотные характеристики цепей

КОМПЛЕКСНЫЕ ФУНКЦИИ ЦЕПИ

 

Основным методом расчета цепей синусоидального тока является метод комплексных амплитуд. В его основе лежит пред­ставление синусоидальных функций через экспоненциальные функции мнимой частоты ƒω:

Применение экспоненциальной функции делает возможным ввести понятие комплексной функции цепи, имеющей исключи­тельно большое значение в теории цепей. Понятие комплексной функции используется для описани линейных цепей, не содержа­щих независимые источники энергии.

В самом общем случае сигнал на выходе (реакция) такой цепи х_вых и сигнал на ее входе (воздействие) х_вх связаны линей­ным дифференциальным уравнением вида

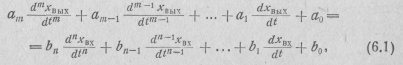
где 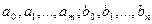— вещественные коэффициенты, за­висящие лишь от параметров цепи и ее схемы. Представим воздействие в виде экспоненты

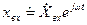.                        (6.2)

Реакция линейной цепи в установившемся режиме, т. е. спустя достаточно большой промежуток времени после появления воздей­ствия, имеет всегда тот же вид, что и воздействие, т. е.

                                     (6.3)

Эти величины представляют токи или напряжения, действую­щие на участках цепи.

Так как дифференцирование экспоненты эквивалентно ее умно­жению на ƒω, после подстановки выражений (6.2) и (6.3) в фор­мулу (6.1) получим

Комплексной функцией цепи называется отношение реакции цепи к воздействию, заданному в виде экспоненциальной функции мнимой частоты ƒω:

Порядок цепи и ее комплексной функции определяется наи­высшей степенью при ƒω в знаменателе выражения (6.5).

С помощью комплексной функции легко найти изображение выходного сигнала как произведение

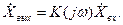
В зависимости от того, рассматривается реакция цепи со сто­роны точек приложения воздействия или же на других ее уча­стках, комплексные функции цепи разделяют на две группы: входные и передаточные.

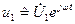Пусть на входных зажимах  пассивной линейной цепи (рис. 6.1) действуют напряжение и ток 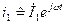.. Выделим в схеме элемент Z₂, на зажимах которого 2 — 2' дей­ствуют напряжение  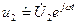и ток .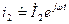

Входной функцией цепи называется отношение изображений тока и напряжения, действующих на входных зажимах. В зави­симости от того, какая величина является воздействием, разли­чают входное сопротивление и входную проводимость:

.           (6.7)
Передаточной функцией цепи называется отношение изобра­жений токов и напряжений, действующих на разных парах зажи­мов. Взависимости от того, что является воздействием, различают:

комплексные передаточные функции или коэффициенты пере­дачи по напряжению и по току:                     

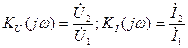;     (6.8)

передаточные сопротивления:

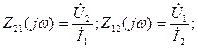   (6.9)

передаточные проводимости:

СВЯЗЬ МЕЖДУ ПАРАМЕТРАМИ ЦЕПИ

И ЕЕ КОМПЛЕКСНЫМИ ФУНКЦИЯМИ

 

Чтобы установить связь между параметрами цепи и ее вход­ными и передаточными комплексными функциями, рассмотрим схему (рис. 6.2).

Пусть к входным зажимам k — k ' пассивной линейной цепи, не содержащей внутренние независимые источники энергии, подклю­чен источник сигнала с э.д. с. I⅛ и внутренним сопротивлением Z_BH. При этом на входе цепи действуют напряжение U⅛ и ток I ⅛, а на выходе, т. е. на любом интересующем нас ее элементе Z \, — напряжение U; и ток I /. Найдем соотношения между этими напря­жениями и токами. Для этого запишем систему уравнений по ме-тоду контурных токов, выбирая ⅛-й и 1-й контуры внешними:

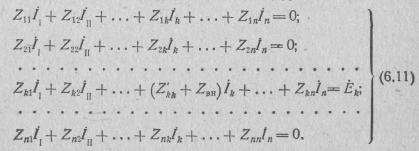
Здесь Z_jj и Z_jk — контурные сопротивления; Z´_kk — сумма со­противлений элементов той части k-го контура, которая входит в состав рассматриваемой цепи и не включает внутреннее conpo-

тивление Z_BH источника;   Z ' _kk + Z_BH = Z_kk — контурное сопро­тивление k-го контура;  

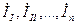 — контурные токи.

Исключим параметры источника сигнала из системы уравне­ний (6.11).

Так как

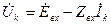, (6.12)

эту систему перепишем в виде:

Ее решение по правилу Крамера относительно выходного тока с последующим разложением определителя Δ _l по l -му столбцу дает

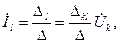  (6.14)

где Δ — определитель системы;

Δ _l — определитель, получающийся из Δ заменой столбца, со­ставленного из коэффициентов Z _kl при неизвестном , столбцом, составленным из свободных членов;

Δ_{k l} — алгебраическое дополнение элемента Z _kl. Аналогично получим решение системы относительно тока на входе

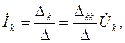 (6.15)

Входные и передаточные функции цепи находим в виде отно­шения определителей системы (6.13), составленной по методу кон­турных токов:

Чтобы выяснить особенности полученных функций, рассмотрим более подробно определители Δ, Δ _kl, Δ _kk.

Общее выражение для определителя п-го порядка системы уравнений (6.13) имеет вид¹

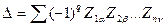
Определитель Δ, таким образом, представляет сумму n! про­изведений. Каждое из этих произведений содержит п множите­лей. Каждый из множителей является элементом определителя и есть не что иное, как соответствующее контурное сопротивление рассматриваемой цепи.

Любое контурное сопротивление, как и сопротивление любой ветви в линейной цепи с конечным числом элементов, в общем случае является рациональной функцией мнимой частоты ƒω:

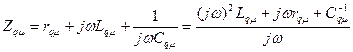 . (6.19)

где .

Так как произведения, суммы, разности и отношения рацио­нальных функций есть также рациональные функции, то и опре­делитель Δ — рациональная функция. То же самое можно сказать и об определителях Δ _kl, Δ _kk, которые отличаются от Δ лишь на единицу меньшим порядком.

Таким образом, убеждаемся, что как входные, так и переда­точные комплексные функции цепи являются рациональными функциями переменной ƒω и в общем виде могут быть представ­лены в виде рациональной дроби (6.5) с вещественными коэффи­циентами. Важно отметить, что все коэффициенты числителя и знаменателя этой дроби вещественные, так как они зависят лишь от схемы цепи и определяются параметрами ее элементов:

Системные функции цепи полностью определяются схемой и параметрами цепи и совершенно не зависят от параметров и схемы источника входного сигнала.

 

¹ Здесь α, ß,..., υ пробегают все возможные n! переста н овок из чисел 1, 2,..., п; знак перед каждым членом определителя (т. е. перед каждым сла­гаемым) определяется числом q инверсий в каждой перестановке.

 

Соотношения (6.11) —(6.18) получены методом контурных то­ков. К аналогичным выражениям и сделанным выводам можно прийти, используя также дуальный метод — метод узловых напря­жений.

Действительно, пусть в схеме (см. рис. 6.2) независимые узлы

выбраны так, что Ù _k и Ù _l — узловые напряжения. Тогда можно записать систему узловых уравнений:

Здесь Y_jj и Y_jk — узловые проводимости; Y ' _kk — сумма прово-димостей ветвей, подходящих k-му узлу ипринадлежащих рас­сматриваемой цепи, взятая без учета источника входного сигнала; (Y ' _{kk +} Y _вн) = Y_kk узловая проводимость k -гoузла;   — узловые напряжения.

Учитывая, что

,                        (6.21)

исключаем параметры источника сигнала из системы уравне­ний (6.20):

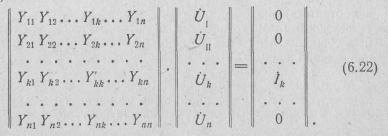
Решая полученную систему относительно Ù _l и Ù _k, спомощью соотношений (6.7) — (6.10) находим функции цепи через опреде­лители системы (6.22), составленной по методу узловых напря­жений:

Так как узловые проводимости

(6.26)

имеют те же свойства, что и контурные сопротивления (6.19), можно прийти к уже сформулированным выше выводам относи­тельно свойств системных функций цепи.

Сравнивая полученные для системных функций выражения (6.16) — (6.18) и (6.23) — (6.26), нужно отметить, что входящие в них определители соответствуют уравнениям, составленным по разным методам. В первом случае они соответствуют матрице контурных сопротивлений (МКС), а во втором — матрице узло­вых проводимостей (МУП).

Важно заметить, что в любых случаях для входных функций

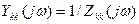(6.27)

а для передаточных функций

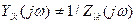,               (6.28)

так как

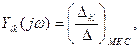но     (6.29)

Для описания цепи, например, системой контурных или узло­вых уравнений используются такие ее параметры, как контурные сопротивления или узловые проводимости. Они определяются зна­чениями сопротивлений элементов, входящих в состав цепи. Эти параметры зависят и от выбора независимых переменных, взятых в качестве определяющих (контурные токи, узловые напряжения), и соответствующих им основных топологических элементов цепи (независимые контуры, узлы), а также от того, какая из возмож­ных совокупностей этих величин и элементов принята для описа­ния данной цепи. Учитывая это обстоятельство, такие параметры называют первичными.

Комплексные функции цепи относятся к числу ее вторичных параметров. Вторичные параметры не зависят от выбора опреде­ляющих величин, выбора независимых контуров или узлов,

КОМПЛЕКСНЫЕ ФУНКЦИИ