Наихудший случай получается, когда при каждом разбиении получаются наиболее неравные части – один элемент и оставшиеся. При выполнении рекурсивных вызовов получается последовательность разбиений из n, n-1, n-2 и т.д. элементов. Поскольку одно разбиение выполняется за линейное время, то вся сортировка выполняется за Θ(n2).
Среднее время работы алгоритма составляет O(n×logn). Поскольку точный анализ несколько трудоёмок, мы его не приводим, найти его можно, например, в [9]. Однако, данную оценку можно пояснить следующими нестрогими соображениями. Предположим, при каждом разбиении исходная последовательность длины n делится на две части длиной (1/K)×n и, соответственно, ((1-K)/K)×n, где K – некоторая константа. В результате получается следующее рекуррентное соотношение:
T(n) = T((1/K)×n) + T(((1-K)/K)×n) + O(n)
Решением данного соотношения будет T(n)=O(n×logn) (см. [9]). При этом данная оценка справедлива, какой бы маленькой не была константа K, то есть как бы сильно не отличались размеры частей разбиений.
Следует сказать, что худший или близкий к нему случай для алгоритма быстрой сортировки очень маловероятен, и на практике данный алгоритм является, пожалуй, самым быстрым алгоритмом сортировки, основанным на сравнениях элементов. При этом он не требует дополнительной памяти за исключением значений, помещаемых в стек при рекурсивных вызовах.
На самом деле худший случай маловероятен, если мы сортируем действительно случайные последовательности. Реальные же данные зачастую такими не являются – они могут быть уже отсортированы, идти в арифметической или геометрической прогрессии и т.п. Наконец, можно даже предположить, что некий злоумышленник (например, автор олимпиадной задачи по программированию) может специально расположить входные данные так, чтобы произошел как раз худший случай и сортировка «вылетела» с переполнением стека или работала за квадратичное время.
Чтобы обезопаситься от этого, используется рандомизированный вариант данного алгоритма: например, перемешиваются случайным образом все элементы в массиве перед выполнением сортировки либо опорный элемент выбирается не каждый раз одинаково, а случайным образом.
Сортировка Шелла
Алгоритм сортировки Шелла представляет собой усовершенствование метода простых вставок, но обеспечивает существенно более высокую скорость работы. Алгоритм работает следующим образом. Вначале выполняется сортировка простыми вставками подпоследовательностей элементов, отстоящих друг от друга на некоторое расстояние hs. Далее аналогичная операция выполняется для hs-1, hs-2, … h1. При этом h1 должен быть равен 1 - это гарантирует корректность сортировки, поскольку на последнем проходе она превращается в обычную сортировку вставками.
Рассмотрим пример. Пусть приращения выглядят следующим образом: h1=1, h2=5, исходная последовательность:
<3,6,2,8,4,2,9,1,5,7,11,0,10,14,8,12>. На первом проходе мы выполняем сортировку подпоследовательностей, элементы которых расположены с шагом 5: <3,2,11,12>, <6,9,0>, <2,1,10>, <8,5,14> и <4,7,8>. В результате исходная последовательность преобразуется к следующей:
<2,0,1,5,4,3,6,2,8,7,11,9,10,14,8,12>.
На втором проходе h1=1, т.е. мы выполняем сортировку вставками всей оставшейся последовательности и получаем окончательный результат:
<0,1,2,2,3,4,5,6,7,8,8,9,10,11,12,14>
На первый взгляд может показаться, что алгоритм Шелла должен работает ещё медленнее, чем обычная сортировка вставками, так как последний проход алгоритма как раз к ней и сводится. На самом деле это не так. Высокую эффективность алгоритма неформально можно пояснить следующим образом. На начальных проходах сортируемые группы сравнительно невелики, но в результате этих проходов значительная часть элементов оказывается вблизи нужных позиций. При росте же длины подпоследовательностей для их сортировки требуется уже сравнительно небольшое число перестановок, так как они тому времени становятся довольно хорошо упорядочены.
При анализе данного алгоритма возникают сложные математические задачи, многие из которых ещё не решены. В частности, неизвестно, какая последовательность приращений даёт наилучшие результаты. Кнут показал, что для большинства случаев хорошим выбором является последовательность h1=1, h2=3h1+1, …, hs=3hs-1+1. Величина s - наименьшее число, такое что hs+2³N, где N – число элементов массива.
Например, для N=1000 нужно взять следующую последовательность приращений (в обратном порядке): 1, 4, 13, 40, 121.
При таком выборе среднее время сортировки составит O(n1.25), время сортировки в наихудшем случае – O(n1.5).
Седжвиком была предложена следующая последовательность приращений:
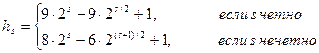
здесь s – наименьшее число, такое что 3×hs+1³N.
При таком выборе время сортировки в худшем случае составляет O(n4/3), в среднем – O(n7/6) [Кнут, том 3].
Пример сортировки Шелла с использованием последовательности Седжвика:
void shellsort(int a[], int n)
{ //заранее просчитанная последовательность приращений Седжвика
const unsigned long h[] =
{1,5,19,41,109,209,505,929,2161,3905,8929,16001,36289,64769,146305,260609,
587521,1045505,2354689,4188161,9427969,16764929,37730305,67084289,150958081,
268386305,603906049,1073643521,2415771649,4294770689};
//определяем начальное приращение
int s;
for(s=0; h[s+1]<n/3; s++);
//цикл по приращениям
for(; s>=0; s--)
{ //выполняем сортировку вставками с шагом h[s].
//Внешний цикл проходит по всем элементам, внутренний цикл
//вставляет элемент на соответствующее место в его группе
int step = h[s];
for(int i=step; i<n; i++)
{ int t = a[i];
int j;
for(j=i-step; (j>=0) && (a[j]>t); j=j-step)
a[j+step] = a[j];
a[j+step]=t;
}
}
}
Хотя асимптотически время работы данного алгоритма и превышает n×logn, но для реальных входных данных (помещающихся в оперативную память современных машин) он вполне способен конкурировать с описанными выше быстрыми способами сортировки.