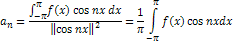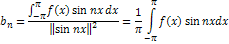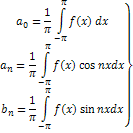Ортогональные и ортонормированные системы функций.
Говорят, что функции 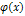 и
и 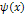 ортогональны на
ортогональны на  , если интеграл
, если интеграл 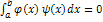 .
.
Система функций 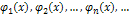 конечная или бесконечная называется ортогональной на
конечная или бесконечная называется ортогональной на  , если функции этой системы попарно ортогональны
, если функции этой системы попарно ортогональны 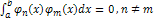 ; при этом будет предполагать, что интеграл
; при этом будет предполагать, что интеграл 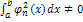 , для всех n-1,2,…
, для всех n-1,2,…
Система функций называется ортонормированной на g w:val="EN-US"/></w:rPr><m:t>b</m:t></m:r></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 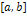 , если
, если 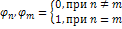 . Если ортогональная система функций
. Если ортогональная система функций 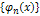 на g w:val="EN-US"/></w:rPr><m:t>b</m:t></m:r></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
на g w:val="EN-US"/></w:rPr><m:t>b</m:t></m:r></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 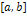 не содержит функций с нулевой нормой, то система
не содержит функций с нулевой нормой, то система 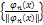 - ортонормированная. Действительно,
- ортонормированная. Действительно, 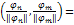
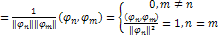 .
.
Ряды Фурье по произвольной ортогональной системе функций.
Пусть 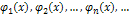 (1) бесконечная ортогональная на
(1) бесконечная ортогональная на 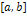 система функций. Предположим, что некоторую функцию
система функций. Предположим, что некоторую функцию 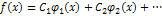
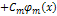 (2) – называется многочленом, где
(2) – называется многочленом, где 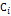 - некоторая константа системы функций (1). Домножим правую и левую часть выражения (2) на
- некоторая константа системы функций (1). Домножим правую и левую часть выражения (2) на 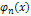 , где
, где 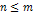 и проинтегрируем правую и левую части на
и проинтегрируем правую и левую части на 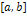 .
. 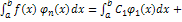
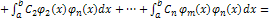
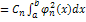 .
.  .
.
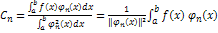 (3). Коэффициент
(3). Коэффициент 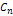 определяемый по формуле (3) называется коэффициентом Фурье для функции
определяемый по формуле (3) называется коэффициентом Фурье для функции  по ортогональной системе функций (1). Определение: Пусть функция
по ортогональной системе функций (1). Определение: Пусть функция  производная, непрерывная или разрывная (допускается разрыв первого рода), заданная на
производная, непрерывная или разрывная (допускается разрыв первого рода), заданная на 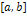 , для которой интегралы вида (3) позволяют вычислить для функции
, для которой интегралы вида (3) позволяют вычислить для функции  коэффициент Фурье с любым n. Ряд вида
коэффициент Фурье с любым n. Ряд вида 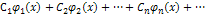 (4), где
(4), где 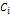 - коэффициенты Фурье, называемые рядом Фурье для функции
- коэффициенты Фурье, называемые рядом Фурье для функции  по системе функции (1), при этом можно записать
по системе функции (1), при этом можно записать 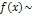 (4). Знак «~» можно поменять на «=», если докозательство сходимости ряда (4) и этот ряд имеют своей суммой функцию
(4). Знак «~» можно поменять на «=», если докозательство сходимости ряда (4) и этот ряд имеют своей суммой функцию  .
.
Ортогональность тригонометрической системы функций.
Система функций 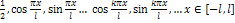 , (1) называется основной тригонометрической системой. Эта система ортогональна на отрезке
, (1) называется основной тригонометрической системой. Эта система ортогональна на отрезке 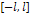 .
.
Можно показать, подсчитав интегралы вида 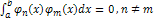 и
и 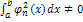 , что система (1) является ортогональной системой на
, что система (1) является ортогональной системой на 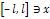 и на любом отрезке оси OX, длиной 2l:
и на любом отрезке оси OX, длиной 2l:
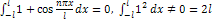 ,
,
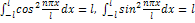 . От системы (1) можно перейти к системе
. От системы (1) можно перейти к системе 
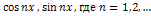 путем замены переменной:
путем замены переменной: 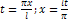 .
.
Формулировка достаточных условий разложимости функции в тригонометрический ряд Фурье.
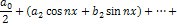
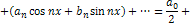
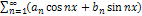 , где
, где 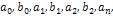
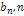 - действительные числа, называемые коэффициентами Фурье. Пусть функция
- действительные числа, называемые коэффициентами Фурье. Пусть функция  произвольная, заданная на
произвольная, заданная на 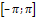 такая, что существуют интегралы:
такая, что существуют интегралы: 
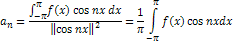
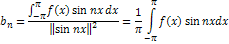
Функцию  можно представить в виде ряда Фурье:
можно представить в виде ряда Фурье: 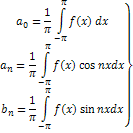
Ортогональные и ортонормированные системы функций.
Говорят, что функции 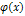 и
и 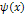 ортогональны на
ортогональны на  , если интеграл
, если интеграл 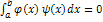 .
.
Система функций 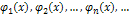 конечная или бесконечная называется ортогональной на
конечная или бесконечная называется ортогональной на  , если функции этой системы попарно ортогональны
, если функции этой системы попарно ортогональны 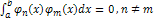 ; при этом будет предполагать, что интеграл
; при этом будет предполагать, что интеграл 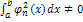 , для всех n-1,2,…
, для всех n-1,2,…
Система функций называется ортонормированной на g w:val="EN-US"/></w:rPr><m:t>b</m:t></m:r></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 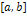 , если
, если 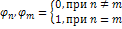 . Если ортогональная система функций
. Если ортогональная система функций 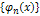 на g w:val="EN-US"/></w:rPr><m:t>b</m:t></m:r></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
на g w:val="EN-US"/></w:rPr><m:t>b</m:t></m:r></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 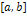 не содержит функций с нулевой нормой, то система
не содержит функций с нулевой нормой, то система 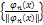 - ортонормированная. Действительно,
- ортонормированная. Действительно, 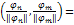
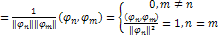 .
.



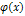 и
и 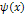 ортогональны на
ортогональны на  , если интеграл
, если интеграл 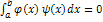 .
.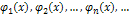 конечная или бесконечная называется ортогональной на
конечная или бесконечная называется ортогональной на 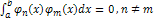 ; при этом будет предполагать, что интеграл
; при этом будет предполагать, что интеграл 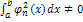 , для всех n-1,2,…
, для всех n-1,2,…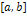 , если
, если 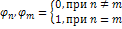 . Если ортогональная система функций
. Если ортогональная система функций 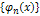 на g w:val="EN-US"/></w:rPr><m:t>b</m:t></m:r></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
на g w:val="EN-US"/></w:rPr><m:t>b</m:t></m:r></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 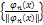 - ортонормированная. Действительно,
- ортонормированная. Действительно, 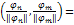
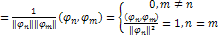 .
.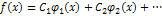
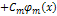 (2) – называется многочленом, где
(2) – называется многочленом, где 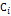 - некоторая константа системы функций (1). Домножим правую и левую часть выражения (2) на
- некоторая константа системы функций (1). Домножим правую и левую часть выражения (2) на 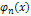 , где
, где 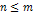 и проинтегрируем правую и левую части на
и проинтегрируем правую и левую части на 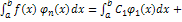
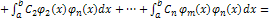
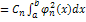 .
.  .
.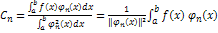 (3). Коэффициент
(3). Коэффициент 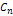 определяемый по формуле (3) называется коэффициентом Фурье для функции
определяемый по формуле (3) называется коэффициентом Фурье для функции  по ортогональной системе функций (1). Определение: Пусть функция
по ортогональной системе функций (1). Определение: Пусть функция 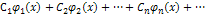 (4), где
(4), где 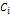 - коэффициенты Фурье, называемые рядом Фурье для функции
- коэффициенты Фурье, называемые рядом Фурье для функции 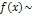 (4). Знак «~» можно поменять на «=», если докозательство сходимости ряда (4) и этот ряд имеют своей суммой функцию
(4). Знак «~» можно поменять на «=», если докозательство сходимости ряда (4) и этот ряд имеют своей суммой функцию 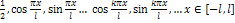 , (1) называется основной тригонометрической системой. Эта система ортогональна на отрезке
, (1) называется основной тригонометрической системой. Эта система ортогональна на отрезке 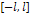 .
.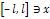 и на любом отрезке оси OX, длиной 2l:
и на любом отрезке оси OX, длиной 2l: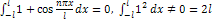 ,
,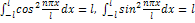 . От системы (1) можно перейти к системе
. От системы (1) можно перейти к системе 
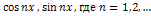 путем замены переменной:
путем замены переменной: 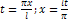 .
.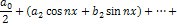
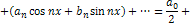
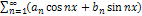 , где
, где 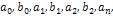
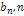 - действительные числа, называемые коэффициентами Фурье. Пусть функция
- действительные числа, называемые коэффициентами Фурье. Пусть функция 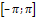 такая, что существуют интегралы:
такая, что существуют интегралы: