МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
РОССИЙСКИЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ Г.В. ПЛЕХАНОВА
ИВАНОВСКИЙ ФИЛИАЛ
Кафедра Математики, экономической информатики
и вычислительной техники
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Методические указания
для самостоятельной работы
студентов 1 курса заочной формы обучения
2014
Составитель В.А.Тимохина
Методические указания по дисциплине «Математический анализ» содержат конспект лекций, решенные задачи и набор задач для самостоятельной работы студентов заочной формы обучения по основам математического анализа.
Содержание
ТЕМА 1. ТЕОРИЯ ПРЕДЕЛОВ.. 4
1.1. Понятие предела функции. 4
1.2. Основные свойства бесконечно малых: 5
1.3. Методы вычисления пределов. 6
1.4. Сравнение бесконечно малых. Эквивалентные бесконечно малые. 7
1.5. Задачи для самостоятельного решения. 9
ТЕМА 2. ПРОИЗВОДНАЯ.. 9
2.1. Определение производной функции одной переменной. 9
2.2. Основные правила дифференцирования. 10
2.3. Нахождение производных. 11
2.4. Задачи для самостоятельного решения. 12
ТЕМА 3. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИИ.. 12
3.1. Возрастание и убывание функции. 12
3.2. Максимум и минимум функции. 13
3.3. Выпуклость и вогнутость кривой. Точки перегиба. 14
3.4. Асимптоты.. 14
3.5.Схема полного исследования функции. 15
3.6. Задачи для самостоятельного решения. 18
ТЕМА 4. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.. 18
4.1. Понятие функции нескольких переменных. 18
4.2. Частные производные функции. 19
4.3. Частные производные высших порядков. 20
4.4. Нахождение экстремума функции. 21
4.5. Задачи для самостоятельного решения. 22
ТЕМА 5. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.. 22
5.1. Первообразная и неопределенный интеграл. 22
5.2. Свойства неопределенного интеграла. 23
5.3. Методы интегрирования. 24
5.3.1.Метод замены переменной. 25
5.3.2. Метод интегрирования по частям.. 25
5.3.3. Интегрирование тригонометрических функций. 25
5.3.4. Интегрирование рациональных дробей с помощью разложения на простейшие дроби (метод неопределенных коэффициентов) 26
5.4. Задачи для самостоятельного решения. 27
ТЕМА 6. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ.. 28
6.1. Понятие определенного интеграла. 28
6.2. Основные свойства определенного интеграла. 29
6.3. Правила вычисления определенного интеграла. 30
6.4. Задачи для самостоятельного решения. 30
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ... 32
ТЕМА 1. ТЕОРИЯ ПРЕДЕЛОВ
Понятие предела функции
Определение. Функция, у которой областью определения является множество натуральных чисел называется последовательностью. 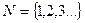 .
.
Определение. Число  называется пределом последовательности
называется пределом последовательности 
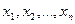 , если для всякого сколь угодно малого положительного числа
, если для всякого сколь угодно малого положительного числа 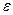 найдется такое положительное число N, что
найдется такое положительное число N, что  при n<N. В этом случае говорят, что
при n<N. В этом случае говорят, что  есть предел последовательности и записывают
есть предел последовательности и записывают
lim 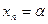 при
при 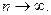 Геометрически это означает, что если для любой наперед заданной как угодно малой окрестности с центром в точке
Геометрически это означает, что если для любой наперед заданной как угодно малой окрестности с центром в точке  и радиусом
и радиусом 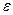 , найдется такое значение x, что все точки, соответствующие последующим значениям переменной, будут находится в этой окрестности.
, найдется такое значение x, что все точки, соответствующие последующим значениям переменной, будут находится в этой окрестности.
Определение. Число А называется пределом функции f (x) при  , если для любого сколь угодно малого
, если для любого сколь угодно малого  , найдется такое
, найдется такое 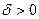 , что
, что 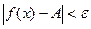 при
при  Это записывается так:
Это записывается так: 

Число f(a-0)= 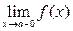 называют левым пределом функции (х принимает только значение меньше а).
называют левым пределом функции (х принимает только значение меньше а).
Число f(a+0)= 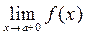 называют правым пределом функции (х принимает только значение больше а).
называют правым пределом функции (х принимает только значение больше а).
Для существования предела функции f(x) при  необходимо и достаточно, чтобы
необходимо и достаточно, чтобы 
Переменная  называется бесконечно малой, если она при изменении по абсолютному значению становится и при дальнейшем изменении остается меньше любого наперед заданного сколь угодно малого положительно числа
называется бесконечно малой, если она при изменении по абсолютному значению становится и при дальнейшем изменении остается меньше любого наперед заданного сколь угодно малого положительно числа 
Переменная x называется бесконечно большой, если она при своем изменении по абсолютному значению становится и при дальнейшем изменении остается больше любого наперед заданного положительного числа N, как бы велико оно ни было: 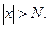
Предел бесконечно малой величины равен нулю (если  бесконечно малая, то lim
бесконечно малая, то lim  =0).
=0).
Разность между переменной и ее пределом есть величина бесконечно малая (если lim x=a, то x-a= 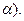
Величина, обратная бесконечно малой, есть бесконечно большая (если  бесконечно малая, то
бесконечно малая, то  бесконечно большая, т.е. если
бесконечно большая, т.е. если 
Величина обратная бесконечно большой, есть бесконечно малая (если x бесконечно большая, то 1/x бесконечно малая, т.е. если 
1.2. Основные свойства бесконечно малых:
1. Алгебраическая сумма любого конечного числа бесконечно малых слагаемых есть величина бесконечно малая.
2. Произведение ограниченной величины на бесконечно малую есть величина бесконечно малая.
Практическое вычисление пределов основывается на следующих теоремах:
Если существуют  и
и 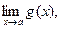 то
то
1. Предел алгебраической суммы определенного числа переменных равен сумме пределов этих переменных


2.Предел произведения равен произведению пределов этих переменных.
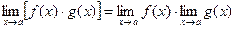
3.Предел частного двух переменных равен частному пределов этих переменных, если предел знаменателя отличен от нуля.
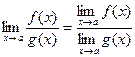 (при
(при  )
)
4.Предел постоянной равен самой постоянной.
5.Постоянный множитель можно выносить за знак предела
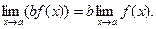
Методы вычисления пределов
1. Вычисление предела функции непосредственной подстановкой предельного значения аргумента в выражении функции.
Если к данной функции, предел которой находится при стремлении аргумента к некоторому предельному значению, применимы теоремы о пределах, то вычисление предела сводится к подстановке этого предельного значения в функцию.
ПРИМЕР 1. 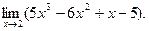
Применив последовательно теоремы о пределах получим:
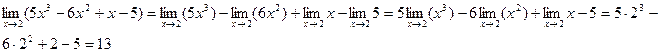 2. Вычисление предела функции, когда предел делителя равен нулю.
2. Вычисление предела функции, когда предел делителя равен нулю.
ПРИМЕР 2. 
Предел делителя равен нулю: 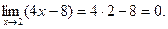 Теорему о пределе частного применить нельзя, т.к. деление на нуль невозможно. Если
Теорему о пределе частного применить нельзя, т.к. деление на нуль невозможно. Если  , то 4x-8 есть величина бесконечно малая, а величина ей обратная
, то 4x-8 есть величина бесконечно малая, а величина ей обратная 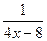 бесконечно большая. Следовательно, при
бесконечно большая. Следовательно, при  произведение
произведение  есть величина бесконечно большая, т.е
есть величина бесконечно большая, т.е 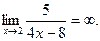
3.Раскрытие неопределенности 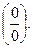
ПРИМЕР 3. 
Предел числителя и знаменателя равен нулю. Вычислить предел функции непосредственной подстановкой вместо аргумента его предельного значения нельзя, так как при  имеем отношение двух бесконечно малых величин (отношение
имеем отношение двух бесконечно малых величин (отношение  не имеет смысла).
не имеет смысла).
Разложим числитель и знаменатель на множители, чтобы сократить дробь на общий множитель, стремящийся к нулю. По определению предела функции аргумент x стремится к своему предельному значению, никогда не принимая этого значения, поэтому до перехода к пределу можно произвести сокращение на множитель, стремящийся к нулю.
Имеем:

4. Вычисление предела функции при 
ПРИМЕР 4. Вычислить 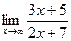
Числитель и знаменатель дроби неограниченно возрастают при  В таком случае говорят, что имеет место неопределенность вида
В таком случае говорят, что имеет место неопределенность вида  . Разделив числитель и знаменатель дроби на x в старшей степени получаем
. Разделив числитель и знаменатель дроби на x в старшей степени получаем
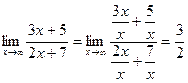 .
.
Т.к. при  каждая из дробей
каждая из дробей  бесконечно малые величины и их пределы равны нулю. Рассмотрим случай, когда при
бесконечно малые величины и их пределы равны нулю. Рассмотрим случай, когда при  уменьшаемое и вычитаемое есть бесконечно большие величины.
уменьшаемое и вычитаемое есть бесконечно большие величины.
ПРИМЕР 5. 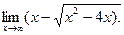

ТЕМА 2. ПРОИЗВОДНАЯ
Нахождение производных
ПРИМЕР 1. y=5x
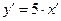
 (т.к.
(т.к. 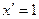 )
)
ПРИМЕР 2. 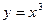

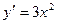
ПРИМЕР 3. 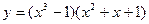
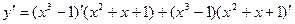
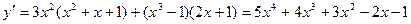
ПРИМЕР 4. 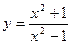

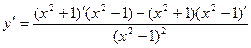

ПРИМЕР 5. 
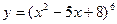
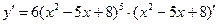
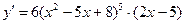
ПРИМЕР 6. 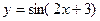

ПРИМЕР 7. 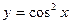
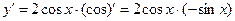
ПРИМЕР 8. 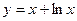
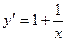
ПРИМЕР 9. 
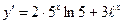
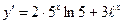
ПРИМЕР 10. 

2.4. Задачи для самостоятельного решения
1.  2.
2. 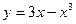
3. 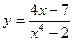 4.
4. 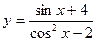
5. 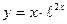 6.
6. 
7.  8.
8. 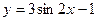
9. 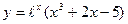 10.
10. 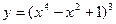
Максимум и минимум функции
Определение. Функция f(x) имеет максимум в точке  , если значение функции f(x) в точке
, если значение функции f(x) в точке  больше, чем ее значения во всех точках некоторого интервала, содержащего точку
больше, чем ее значения во всех точках некоторого интервала, содержащего точку  . Иначе говоря, функция f(x) имеет максимум при
. Иначе говоря, функция f(x) имеет максимум при  , если при всех x, достаточно близких к
, если при всех x, достаточно близких к  , выполняется неравенство
, выполняется неравенство 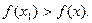
Определение. Функция f(x) в точке  имеет минимум, если значение функции f(x) в точке
имеет минимум, если значение функции f(x) в точке  меньше, чем ее значения во всех точках некоторого интервала, содержащего точку
меньше, чем ее значения во всех точках некоторого интервала, содержащего точку  . Иначе говоря, если выполняется неравенство
. Иначе говоря, если выполняется неравенство 
Максимум и минимум функции называют экстремумами. Экстремальные значения функции и их расположение на отрезке  в известной степени характеризуют изменение функции в зависимости от изменения аргумента.
в известной степени характеризуют изменение функции в зависимости от изменения аргумента.
Теорема 1. (необходимое условие экстремума)
Если дифференцируемая функция y=f(x) имеет в точке  максимум (max) или минимум (min), то ее производная обращается в нуль в этой точке, т.е.
максимум (max) или минимум (min), то ее производная обращается в нуль в этой точке, т.е. 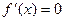 , точка
, точка  в этом случае называется критической точкой.
в этом случае называется критической точкой.
Если производная не существует в какой-либо точке, то в этой точке производная терпит разрыв.
Теорема 2. (достаточное условие существования экстремума)
Пусть функция f(x) непрерывна в некотором интервале, содержащем критическую точку  и дифференцируема во всех точках этого интервала (кроме самой точки
и дифференцируема во всех точках этого интервала (кроме самой точки  ). Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то при
). Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то при  функция имеет максимум. Если же меняет знак с минуса на плюс, то функция имеет в этой точке минимум.
функция имеет максимум. Если же меняет знак с минуса на плюс, то функция имеет в этой точке минимум.
ПРИМЕР 2. Найти экстремумы функции 
1. Найдем производную функции 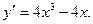
2. Определим критические точки, для этого приравняем производную к нулю. 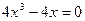



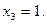
Функция определена и непрерывна на всей числовой прямой, точки 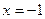 ,
,  ,
, 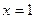 являются критическими.
являются критическими.
3. Исследуем критические точки, определяя знак производной слева и справа от каждой из них, для этого наносим точки на числовую ось и определяем знак производной внутри каждого интервала.
На интервале 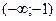
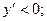
На интервале 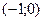
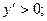
На интервале 
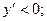
На интервале 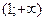
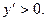
При переходе через точки 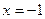 ,
, 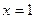 знак производной сменился с (-) на (+), Следовательно, в этих точках функция имеет минимум (min), а при переходе через точку x=0 знак производной сменился с (+) на (-), следовательно в этой точке функция имеет максимум (max).
знак производной сменился с (-) на (+), Следовательно, в этих точках функция имеет минимум (min), а при переходе через точку x=0 знак производной сменился с (+) на (-), следовательно в этой точке функция имеет максимум (max).
4. Найдем значение функции в этих точках

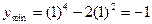
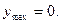
Асимптоты
Прямая а называется асимптотой графика функции y=f(x), если расстояние между точками графика и прямой стремится к нулю по мере удаления графика от начала координат.
Различают вертикальные, наклонные и горизонтальные асимптоты.
1. Вертикальные асимптоты - это прямые параллельные оси ординат. Их следует искать в точках разрыва функции или на концах её области определения (а,b), если а,b -конечные числа, т.е. нужно найти такие значения x=a, при приближении к которым функция y=f(x) стремится к бесконечности (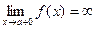 или
или  или
или 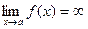 ).
).
2. Наклонные асимптоты. Уравнение наклонной асимптоты имеет вид 
Необходимо определить числа k и b. Они находятся по формулам:  ,
,  В том случае, если
В том случае, если 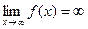 , функция тоже может иметь наклонную асимптоту.
, функция тоже может иметь наклонную асимптоту.
3. Горизонтальные асимптоты - это прямые параллельные оси абсцисс. Уравнение имеет вид y= b. Число b находится по формуле  .
.
Замечание: функция может иметь правостороннюю или левостороннюю горизонтальную асимптоту, в зависимости от 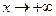 или
или 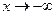
Частные производные функции
Частной производной от функции z=f(x,y) по независимой переменной x называется конечный предел, 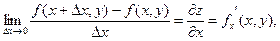
вычисленный при постоянном y.
Частной производной по независимой переменной y называется конечный предел,  вычисленный при постоянном x.
вычисленный при постоянном x.
При нахождении частных производных по одной из переменных, остальные считаются const. Для частных производных справедливы обычные правила и формулы дифференцирования.
Правила вычисления частных производных совпадают с правилами вычисления производной для функции одной переменной и только требуется помнить, по какой переменной ищется производная.
ПРИМЕР 1.
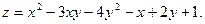 Найти
Найти  и
и 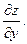
Рассмотрим y как постоянную величину, получим
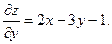
Рассмотрим x как постоянную величину, получим

ПРИМЕР 2.
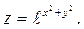 Найти
Найти  и
и 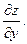


Методы интегрирования
ПРИМЕР 1. 
 используя свойство 3,формулу 3 и 1 из таблицы производных получим
используя свойство 3,формулу 3 и 1 из таблицы производных получим 
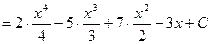 .
.
Метод замены переменной
ПРИМЕР 2. ∫ 
Положим  =1-2х, тогда х =
=1-2х, тогда х = 
 ,
, 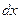 =
=  (
(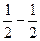
 )=(
)=(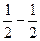
 )´
)´ 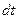 =-
=- 
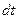 и
и
∫  = ∫
= ∫ 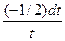 =-
=-  ∫
∫  =-
=- 
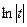 +С=-
+С=- 
 │1-2х │+С.
│1-2х │+С.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Высшая математика для экономистов: учебник. – 3-е изд. / Под. ред. Н.Ш. Кремера – М.: ЮНИТИ, 2006. – 480 с.
2. Красс, М.С. Математика для экономического бакалавриата: учебник / М.С. Красс, Б.П. Чупрынов. – М.: ИНФРА-М, 2011. – 472 с, (Гриф) //ЭБС znanium.com/ ООО Издательский Дом ИНФРА-М (RU)
3. Математика для экономистов: от арифметики до эконометрики: учебно-справочное пособие / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин; под ред. Н.Ш. Кремера. – 2-е изд., перераб. и доп. – М.: Юрайт, 2010. – 646 с. – Предм. указ.: с.613-646. – ISBN 978-5-9916-0582-3.
4. Скрыдлова, Е.В. Линейная алгебра: учебное пособие / Е.В. Скрыдло- ва, О.О. Белова. – Ростов-на-Дону: Феникс, 2012. – 142 с. – Библиогр.: с.139. – ISBN 978-5-222-19713-4.
5. Шевцов, Г.С. Линейная алгебра: теория и прикладные аспекты: Учебное пособие / Г.С. Шевцов. – 2-e изд., испр. и доп. – М.: Магистр: ИН- ФРА-М, 2010. – 528 с, (Гриф) //ЭБС znanium.com/ ООО Издательский Дом ИНФРА-М (RU)
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
РОССИЙСКИЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ Г.В. ПЛЕХАНОВА
ИВАНОВСКИЙ ФИЛИАЛ
Кафедра Математики, экономической информатики
и вычислительной техники
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Методические указания
для самостоятельной работы
студентов 1 курса заочной формы обучения
2014
Составитель В.А.Тимохина
Методические указания по дисциплине «Математический анализ» содержат конспект лекций, решенные задачи и набор задач для самостоятельной работы студентов заочной формы обучения по основам математического анализа.
Содержание
ТЕМА 1. ТЕОРИЯ ПРЕДЕЛОВ.. 4
1.1. Понятие предела функции. 4
1.2. Основные свойства бесконечно малых: 5
1.3. Методы вычисления пределов. 6
1.4. Сравнение бесконечно малых. Эквивалентные бесконечно малые. 7
1.5. Задачи для самостоятельного решения. 9
ТЕМА 2. ПРОИЗВОДНАЯ.. 9
2.1. Определение производной функции одной переменной. 9
2.2. Основные правила дифференцирования. 10
2.3. Нахождение производных. 11
2.4. Задачи для самостоятельного решения. 12
ТЕМА 3. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИИ.. 12
3.1. Возрастание и убывание функции. 12
3.2. Максимум и минимум функции. 13
3.3. Выпуклость и вогнутость кривой. Точки перегиба. 14
3.4. Асимптоты.. 14
3.5.Схема полного исследования функции. 15
3.6. Задачи для самостоятельного решения. 18
ТЕМА 4. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.. 18
4.1. Понятие функции нескольких переменных. 18
4.2. Частные производные функции. 19
4.3. Частные производные высших порядков. 20
4.4. Нахождение экстремума функции. 21
4.5. Задачи для самостоятельного решения. 22
ТЕМА 5. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.. 22
5.1. Первообразная и неопределенный интеграл. 22
5.2. Свойства неопределенного интеграла. 23
5.3. Методы интегрирования. 24
5.3.1.Метод замены переменной. 25
5.3.2. Метод интегрирования по частям.. 25
5.3.3. Интегрирование тригонометрических функций. 25
5.3.4. Интегрирование рациональных дробей с помощью разложения на простейшие дроби (метод неопределенных коэффициентов) 26
5.4. Задачи для самостоятельного решения. 27
ТЕМА 6. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ.. 28
6.1. Понятие определенного интеграла. 28
6.2. Основные свойства определенного интеграла. 29
6.3. Правила вычисления определенного интеграла. 30
6.4. Задачи для самостоятельного решения. 30
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ... 32
ТЕМА 1. ТЕОРИЯ ПРЕДЕЛОВ
Понятие предела функции
Определение. Функция, у которой областью определения является множество натуральных чисел называется последовательностью. 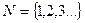 .
.
Определение. Число  называется пределом последовательности
называется пределом последовательности 
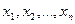 , если для всякого сколь угодно малого положительного числа
, если для всякого сколь угодно малого положительного числа 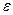 найдется такое положительное число N, что
найдется такое положительное число N, что  при n<N. В этом случае говорят, что
при n<N. В этом случае говорят, что  есть предел последовательности и записывают
есть предел последовательности и записывают
lim 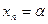 при
при 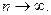 Геометрически это означает, что если для любой наперед заданной как угодно малой окрестности с центром в точке
Геометрически это означает, что если для любой наперед заданной как угодно малой окрестности с центром в точке  и радиусом
и радиусом 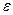 , найдется такое значение x, что все точки, соответствующие последующим значениям переменной, будут находится в этой окрестности.
, найдется такое значение x, что все точки, соответствующие последующим значениям переменной, будут находится в этой окрестности.
Определение. Число А называется пределом функции f (x) при  , если для любого сколь угодно малого
, если для любого сколь угодно малого  , найдется такое
, найдется такое 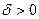 , что
, что 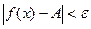 при
при  Это записывается так:
Это записывается так: 

Число f(a-0)= 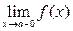 называют левым пределом функции (х принимает только значение меньше а).
называют левым пределом функции (х принимает только значение меньше а).
Число f(a+0)= 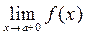 называют правым пределом функции (х принимает только значение больше а).
называют правым пределом функции (х принимает только значение больше а).
Для существования предела функции f(x) при  необходимо и достаточно, чтобы
необходимо и достаточно, чтобы 
Переменная  называется бесконечно малой, если она при изменении по абсолютному значению становится и при дальнейшем изменении остается меньше любого наперед заданного сколь угодно малого положительно числа
называется бесконечно малой, если она при изменении по абсолютному значению становится и при дальнейшем изменении остается меньше любого наперед заданного сколь угодно малого положительно числа 
Переменная x называется бесконечно большой, если она при своем изменении по абсолютному значению становится и при дальнейшем изменении остается больше любого наперед заданного положительного числа N, как бы велико оно ни было: 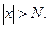
Предел бесконечно малой величины равен нулю (если  бесконечно малая, то lim
бесконечно малая, то lim  =0).
=0).
Разность между переменной и ее пределом есть величина бесконечно малая (если lim x=a, то x-a= 
Величина, обратная бесконечно малой, есть бесконечно большая (если  бесконечно малая, то
бесконечно малая, то  бесконечно большая, т.е. если
бесконечно большая, т.е. если 
Величина обратная бесконечно большой, есть бесконечно малая (если x бесконечно большая, то 1/x бесконечно малая, т.е. если 
1.2. Основные свойства бесконечно малых:
1. Алгебраическая сумма любого конечного числа бесконечно малых слагаемых есть величина бесконечно малая.
2. Произведение ограниченной величины на бесконечно малую есть величина бесконечно малая.
Практическое вычисление пределов основывается на следующих теоремах:
Если существуют  и
и 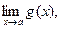 то
то
1. Предел алгебраической суммы определенного числа переменных равен сумме пределов этих переменных


2.Предел произведения равен произведению пределов этих переменных.
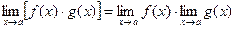
3.Предел частного двух переменных равен частному пределов этих переменных, если предел знаменателя отличен от нуля.
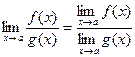 (при
(при  )
)
4.Предел постоянной равен самой постоянной.
5.Постоянный множитель можно выносить за знак предела
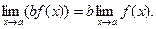
Методы вычисления пределов
1. Вычисление предела функции непосредственной подстановкой предельного значения аргумента в выражении функции.
Если к данной функции, предел которой находится при стремлении аргумента к некоторому предельному значению, применимы теоремы о пределах, то вычисление предела сводится к подстановке этого предельного значения в функцию.
ПРИМЕР 1. 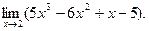
Применив последовательно теоремы о пределах получим:
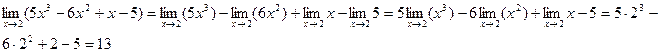 2. Вычисление предела функции, когда предел делителя равен нулю.
2. Вычисление предела функции, когда предел делителя равен нулю.
ПРИМЕР 2. 
Предел делителя равен нулю: 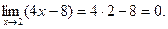 Теорему о пределе частного применить нельзя, т.к. деление на нуль невозможно. Если
Теорему о пределе частного применить нельзя, т.к. деление на нуль невозможно. Если  , то 4x-8 есть величина бесконечно малая, а величина ей обратная
, то 4x-8 есть величина бесконечно малая, а величина ей обратная 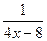 бесконечно большая. Следовательно, при
бесконечно большая. Следовательно, при  произведение
произведение  есть величина бесконечно большая, т.е
есть величина бесконечно большая, т.е 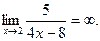
3.Раскрытие неопределенности 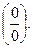
ПРИМЕР 3. 
Предел числителя и знаменателя равен нулю. Вычислить предел функции непосредственной подстановкой вместо аргумента его предельного значения нельзя, так как при  имеем отношение двух бесконечно малых величин (отношение
имеем отношение двух бесконечно малых величин (отношение  не имеет смысла).
не имеет смысла).
Разложим числитель и знаменатель на множители, чтобы сократить дробь на общий множитель, стремящийся к нулю. По определению предела функции аргумент x стремится к своему предельному значению, никогда не принимая этого значения, поэтому до перехода к пределу можно произвести сокращение на множитель, стремящийся к нулю.
Имеем:

4. Вычисление предела функции при 
ПРИМЕР 4. Вычислить 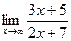
Числитель и знаменатель дроби неограниченно возрастают при  В таком случае говорят, что имеет место неопределенность вида
В таком случае говорят, что имеет место неопределенность вида  . Разделив числитель и знаменатель дроби на x в старшей степени получаем
. Разделив числитель и знаменатель дроби на x в старшей степени получаем
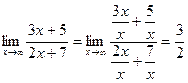 .
.
Т.к. при  каждая из дробей
каждая из дробей  бесконечно малые величины и их пределы равны нулю. Рассмотрим случай, когда при
бесконечно малые величины и их пределы равны нулю. Рассмотрим случай, когда при  уменьшаемое и вычитаемое есть бесконечно большие величины.
уменьшаемое и вычитаемое есть бесконечно большие величины.
ПРИМЕР 5. 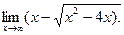

Сравнение бесконечно малых. Эквивалентные бесконечно малые
Для сравнения между собой двух бесконечно малых  и
и 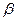 находится предел их отношения. Если при этом окажется, что
находится предел их отношения. Если при этом окажется, что
1) 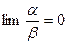 , то
, то  есть бесконечно малая высшего порядка по сравнению с
есть бесконечно малая высшего порядка по сравнению с 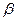 ;
;
2)  то
то  есть бесконечно малая низшего порядка малости по сравнению с
есть бесконечно малая низшего порядка малости по сравнению с 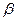 ;
;
3)  a, (а-постоянное, а
a, (а-постоянное, а 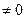 ), то
), то  есть бесконечно малая того же порядка малости, что и
есть бесконечно малая того же порядка малости, что и 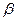 ;
;
4) 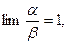 то
то  и
и 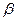 - эквивалентные бесконечно малые.
- эквивалентные бесконечно малые.
При вычислении предела отношения двух бесконечно малых можно каждую (или только одну) из них заменить другой бесконечно малой, ей эквивалентной.
Первый замечательный предел 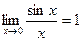
Второй замечательный предел 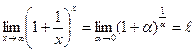
ПРИМЕР 6.
 где
где  - бесконечно малая высшего порядка малости по сравнению с x.
- бесконечно малая высшего порядка малости по сравнению с x.
ПРИМЕР 7. Вычислить предел используя свойство первого замечательного предела 
Умножим числитель и знаменатель на 3. Имеем:
 где sin3x – бесконечно малая того же порядка малости, что и x.
где sin3x – бесконечно малая того же порядка малости, что и x.
ПРИМЕР 8. Вычислить предел 
Воспользуемся вторым замечательным пределом, для этого выполним следующие преобразования:

1.5. Задачи для самостоятельного решения
Вычислить пределы
1. 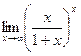 (отв.
(отв.  )
)
3.  (отв. -3)
(отв. -3)
5.  (отв. 2)
(отв. 2)
7.  (отв.
(отв. 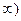
9.  (отв.
(отв.  )
)
11.  (отв. 1)
(отв. 1)
13. 
|
|
|



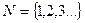 .
. называется пределом последовательности
называется пределом последовательности 
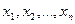 , если для всякого сколь угодно малого положительного числа
, если для всякого сколь угодно малого положительного числа 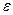 найдется такое положительное число N, что
найдется такое положительное число N, что  при n<N. В этом случае говорят, что
при n<N. В этом случае говорят, что 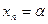 при
при 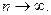 Геометрически это означает, что если для любой наперед заданной как угодно малой окрестности с центром в точке
Геометрически это означает, что если для любой наперед заданной как угодно малой окрестности с центром в точке  , если для любого сколь угодно малого
, если для любого сколь угодно малого  , найдется такое
, найдется такое 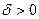 , что
, что 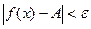 при
при  Это записывается так:
Это записывается так: 
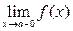 называют левым пределом функции (х принимает только значение меньше а).
называют левым пределом функции (х принимает только значение меньше а).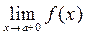 называют правым пределом функции (х принимает только значение больше а).
называют правым пределом функции (х принимает только значение больше а).

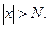
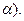
 бесконечно большая, т.е. если
бесконечно большая, т.е. если 

 и
и 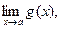 то
то
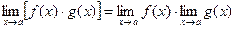
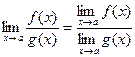 (при
(при  )
)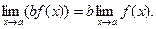
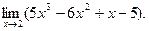
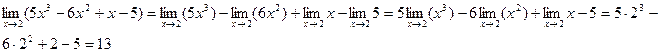 2. Вычисление предела функции, когда предел делителя равен нулю.
2. Вычисление предела функции, когда предел делителя равен нулю.
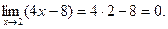 Теорему о пределе частного применить нельзя, т.к. деление на нуль невозможно. Если
Теорему о пределе частного применить нельзя, т.к. деление на нуль невозможно. Если  , то 4x-8 есть величина бесконечно малая, а величина ей обратная
, то 4x-8 есть величина бесконечно малая, а величина ей обратная 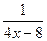 бесконечно большая. Следовательно, при
бесконечно большая. Следовательно, при  произведение
произведение  есть величина бесконечно большая, т.е
есть величина бесконечно большая, т.е 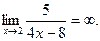
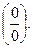

 имеем отношение двух бесконечно малых величин (отношение
имеем отношение двух бесконечно малых величин (отношение  не имеет смысла).
не имеет смысла).

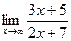
 . Разделив числитель и знаменатель дроби на x в старшей степени получаем
. Разделив числитель и знаменатель дроби на x в старшей степени получаем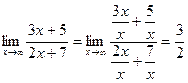 .
. каждая из дробей
каждая из дробей  бесконечно малые величины и их пределы равны нулю. Рассмотрим случай, когда при
бесконечно малые величины и их пределы равны нулю. Рассмотрим случай, когда при 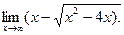

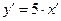
 (т.к.
(т.к. 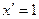 )
)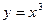

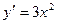
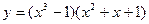
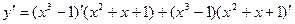
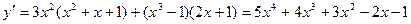
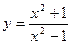
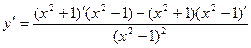

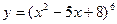
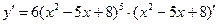
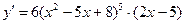
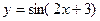

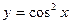
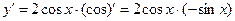
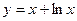
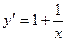

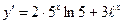


 2.
2. 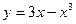
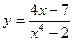 4.
4. 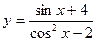
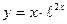 6.
6. 
 8.
8. 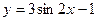
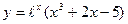 10.
10. 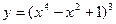
 , если значение функции f(x) в точке
, если значение функции f(x) в точке  , если при всех x, достаточно близких к
, если при всех x, достаточно близких к 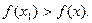

 в известной степени характеризуют изменение функции в зависимости от изменения аргумента.
в известной степени характеризуют изменение функции в зависимости от изменения аргумента.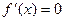 , точка
, точка 
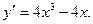
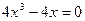



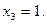
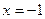 ,
,  ,
, 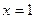 являются критическими.
являются критическими.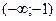
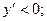
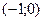
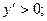

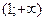
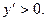

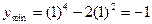
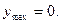
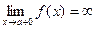 или
или  или
или 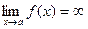 ).
).
 ,
,  В том случае, если
В том случае, если 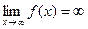 , функция тоже может иметь наклонную асимптоту.
, функция тоже может иметь наклонную асимптоту. .
.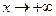 или
или 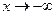
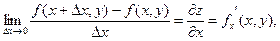
 вычисленный при постоянном x.
вычисленный при постоянном x.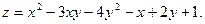 Найти
Найти  и
и 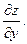
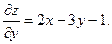

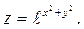 Найти
Найти 


 используя свойство 3,формулу 3 и 1 из таблицы производных получим
используя свойство 3,формулу 3 и 1 из таблицы производных получим 
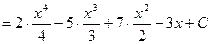 .
.
 =1-2х, тогда х =
=1-2х, тогда х = 
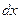 =
=  (
(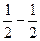
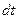 =-
=- 
 = ∫
= ∫ 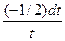 =-
=-  =-
=- 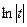 +С=-
+С=-  │1-2х │+С.
│1-2х │+С. 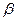 находится предел их отношения. Если при этом окажется, что
находится предел их отношения. Если при этом окажется, что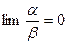 , то
, то  то
то  a, (а-постоянное, а
a, (а-постоянное, а 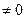 ), то
), то 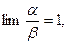 то
то 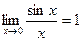
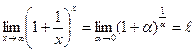
 где
где  - бесконечно малая высшего порядка малости по сравнению с x.
- бесконечно малая высшего порядка малости по сравнению с x.
 где sin3x – бесконечно малая того же порядка малости, что и x.
где sin3x – бесконечно малая того же порядка малости, что и x.

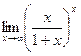 (отв.
(отв.  )
) (отв. -3)
(отв. -3) (отв. 2)
(отв. 2) (отв.
(отв. 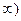
 (отв.
(отв.  (отв. 1)
(отв. 1)

