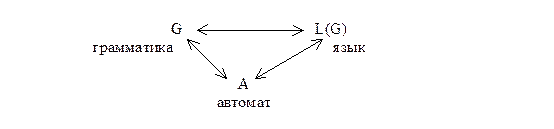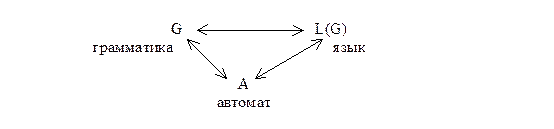Теория формальных языков. Грамматики

ФОРМАЛЬНОЕ ОПРЕДЕЛЕНИЕ

Общение на каком-либо языке – искусственном или естественном- заключается в обмене предложениями или, точнее, фразами. Фраза - это конечная последовательность слов языка. Фразы необходимо уметь строить и распознавать.

Если существует механизм построения фраз и механизм признания их корректности и понимания (механизм распознавания), то мы говорим о существовании некоторой теории рассматриваемого языка.

Определение: Язык L - это множество цепочек конечной длины в алфавите S.

Возникает вопрос – каким образом можно задать язык? Во-первых, язык можно задать полным его перечислением. С точки зрения математики это вовсе не является полной бессмысленностью. А во-вторых, можно иметь некоторое конечное описание языка.

Одним из наиболее эффективных способов описания языка является грамматика. Строго говоря, грамматика - это математическая система, определяющая язык. Как мы убедимся далее, грамматика пригодна не только для задания (или генерации) языка, но и для его распознавания.

Далее нам потребуются некоторые термины и обозначения. Начнем с определения замыкания множества.

Если å - множество (алфавит или словарь), то å^* - замыкание множества å, или, иначе, свободный моноид, порожденный å, т.е. множество всех конечных последовательностей, составленных из элементов множества å, включая и пустую последовательность.

Например, пусть A = {a, b, c}. Тогда A*={e, a, b, c, aa, ab, ac, bb, bc, cc, …}. Здесь e – это пустая последовательность.

Символом å⁺ мы будем обозначать положительное замыкание множества å (или, иначе, свободную полугруппу, порожденную множеством å). В отличие от свободного моноида в положительное замыкание не входит пустая последовательность.

Теперь все готово к тому, чтобы дать основное определение.

Определение. Грамматика - это четверка G = (N, S,P,S), где

N - конечное множество нетерминальных символов (синтаксические переменные или синтаксические категории);

S - конечное множество терминальных символов (слов) (SÇN=Æ);

P - конечное подмножество множества

(NÈS)^*N(NÈS)^* ´ (NÈS)^*

Элемент (a,b) множества P называется правилом или продукцией и записывается в виде a®b;

S - выделенный символ из N (SÎN), называемый начальным символом (эта особая переменная называется также "начальной переменной" или "исходным символом").

Пример:

G = ({A,S},{0,1},P,S),

P = (S®0A1, 0A®00A1, A®e)

 

Определение. Язык, порождаемый грамматикой G (обозначим его через L(G)) - это множество терминальных цепочек, порожденных грамматикой G.

Или, иначе, язык L, порождаемый (распознаваемый) грамматикой, есть множество последовательностей (слов), которые

(3) состоят лишь из терминальных символов;

(4) можно породить, начиная с символа S.

И опять нам требуются определения и обозначения:

Определение: Пусть G = (N, S, P, S). Отношение Þ_G на множестве (NÈS)^* называется непосредственной выводимостью jÞ_Gy (y непосредственно выводима из j), если abg - цепочка из (NÈS)^* и b®d - правило из P, то abgÞ_Gadg.

Транзитивное замыкание отношения Þ_G обозначим через Þ⁺_G.

Запись jÞ⁺_G y означает: y выводима из j нетривиальным образом.

Рефлексивное и транзитивное замыкание отношения Þ_G обозначим через Þ^*_G. Запись jÞ^*_G y означает: y выводима из j. (Если Þ^* - это рефлексивное и транзитивное замыкание отношения Þ, то последовательность a₁Þa₂, a₂Þa₃,.., a_m-1Þa_m, где a_iÎ(NÈS)^*, записывается так: a₁Þ^*a_m.)

 

При этом предполагалось наличие следующих определений:

Определение A. k-я степень отношения R на множестве A (R^k):

(1) aR¹b тогда и только тогда, когда aRb (или R¹ºR);

(2) aRⁱb для i>1 тогда и только тогда, когда $ cÎA: aRc и cR^i-1b.

Определение B. Транзитивное замыкание отношения R на множестве A (R⁺):

aR⁺b тогда и только тогда, когда aRⁱb для некоторого i>0.

Определение C. Рефлексивное и транзитивное замыкание отношения R на множестве A (R^*):

(1) aR^*a для " aÎA;

(2) aR^*b, если aR⁺b

 

Таким образом, получаем формальное определение языка L:

L(G)={ w | w Î å ^*, S Þ ^* w }

 

Нормальная форма Бэкуса-Наура. Нормальная форма Бэкуса-Наура (НФБ или БНФ) служит для описания правил грамматики. Она была впервые применена Науром при описании синтаксиса языка Фортран. По сути БНФ является альтернативной, более упрощенной, менее строгой и потому более распространенной формой записи грамматики. Далее мы будем пользоваться ею наравне с формальными определениями в силу ее большей наглядности.

Пример:

<число>::= <чс>

<чс>::= <чс><цифра>|<цифра>

<цифра>::= 0|1|...|9

ИЕРАРХИЯ ХОМСКОГО

Вернемся к определению грамматики как четверки вида G = (N, å, P, S), где нас интересует вид правил P, под которыми понимается конечное подмножество множества

(NÈS)^*N(NÈS)^* ´ (NÈS)^*

В зависимости от конкретики реализаций правил P существует следующая классификация грамматик (в порядке убывания общности вида правил):

Грамматика типа 0: Правила этой грамматики определяются в самом общем виде.

P: xUy®z

Для распознавания языков, порожденных этими грамматиками, используются т.н. машины Тьюринга – очень мощные (на практике практически неприменимые) математические модели.

Грамматика типа 1: Контекстно-зависимые (чувствительные к контексту)

P: xUy®xuy

Грамматика типа 2: Контекстно-свободные. Распознаются стековыми автоматами (автоматами с магазинной памятью)

P: U®u

Грамматика типа 3: Регулярные грамматики. Распознаются конечными автоматами

P: U®a или U®aA

При этом приняты следующие обозначения:

u Î (NÈS)⁺

x, y, z Î (NÈS)^*

A,U Î N

a Î S

Условно иерархию Хомского можно изобразить так:

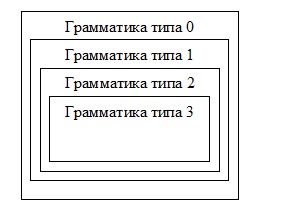
Итак, иерархия Хомского необходима для классификации грамматик по степени их общности. При этом, как видно,

Грамматика типа 0 - самая сложная, никаких ограничений на вид правил в ней не накладывается.

Грамматика типа 1 – контекстно-зависимая; в ней возможность замены цепочки символов может определяться ее (т.е. цепочки) контекстом.

Грамматика типа 2 – контекстно-свободная; в левой части нетерминалы меняются на что угодно.

Грамматика типа 3 - регулярная грамматика, самая ограниченная, самая простая.

РЕГУЛЯРНЫЕ ГРАММАТИКИ

Начнем изучение грамматик с самого простого и самого ограниченного их типа – регулярных грамматик. Вот некоторые примеры:

Идентификатор (в форме БНФ)

<идент>::= <бкв>

<идент>::= <идент><бкв>

<идент>::= <идент><цфр>

<бкв>::= a|b|...|z

<цфр>::= 0|1|...|9

Арифметическое выражение (без скобок)

G = (N, å,P,S)

N={S,E,op,i}

å={<число>, <идент>,+,-,*,/}

P={S®i

S®iE

E®op S

op®+

op®-

op®*

op®/

i®<число>

i®<идент>}

Ту же грамматику бесскобочных выражений можно изобразить в виде БНФ (это не совсем строго, зато весьма наглядно):

<expr>::= <число>|<идент>

<expr>::= <expr><op><expr>

<op>::= +|-|*|/

<число>::= <цфр>

<число>::= <число><цфр>

Еще один пример:

Z::= U0 | V1

U::= Z1 | 1

V::= Z0 | 0

Порождаемый этой грамматикой язык состоит из последовательностей, образуемых парами 01 или 10, т.е. L(G) = { Bⁿ | n > 0}, где B = { 01, 10}.

Стоит, однако, рассмотреть чуть более сложный объект (например, арифметические выражения со скобками), как регулярные грамматики оказываются слишком ограниченными:

Арифметическое выражение (со скобками)

G₀=({E,T,F},{a,+,*,(,),#},P,E)

P = { E ® E+T|T

T ® T*F|F

F ® (E)|a}

Это, разумеется, уже не регулярная, а контекстно-свободная грамматика.

Тем не менее регулярные грамматики играют очень важную роль в теории компиляторов. По крайней мере их достаточно для того, чтобы реализовать первую часть компилятора – сканер. Ведь сканер имеет дело именно с такими простыми объектами, как идентификаторы и константы.

Итак, будем считать, что мы как минимум умеем порождать фразы регулярных языков. Однако все-таки нашей основной задачей является не порождение, а распознавание фраз. Поэтому далее рассмотрим один из наиболее эффективных распознающих механизмов – конечный автомат.

КОНЕЧНЫЕ АВТОМАТЫ

ФОРМАЛЬНОЕ ОПРЕДЕЛЕНИЕ

Как уже говорилось выше, грамматика - это порождающая система. Автомат - это формальная воспринимающая система (или акцептор). Правила автомата определяют принадлежность входной формы данному языку, т.е. автомат – это система, которая распознает принадлежность фразы к тому или иному языку.

Говорят, что автомат эквивалентен данной грамматике, если он воспринимает весь порождаемый ею язык и только этот язык. Как и грамматики, автоматы определяются конечными алфавитами и правилами переписывания.

Определение. Конечный автомат (КА) - это пятерка КА = (å,Q,q₀,T,P), где

å - входной алфавит (конечное множество, называемое также входным словарем);

Q - конечное множество состояний;

q₀ - начальное состояние (q₀ÎQ);

T - множество терминальных (заключительных) состояний, TÌQ;

P – подмножество отображения вида Q´å®Q, называемое функцией переходов. Элементы этого отображения называются правилами и обозначаются как

q_ia_k®q_j, где q_i и q_j - состояния, a_k - входной символ: q_i, q_j Î Q, a_kÎå.

КА можно рассматривать как машину, которая в каждый момент времени находится в некотором состоянии qÎQ и читает поэлементно последовательность w символов из å, записанную на конечной слева ленте. При этом читающая головка машины двигается в одном направлении (слева направо), либо лента перемещается (справа налево). Если автомат в состоянии q_i читает символ a_k и правило q_ia_k®q_j принадлежит P, то автомат воспринимает этот символ и переходит в состояние q_j для обработки следующего символа:

 

Таким образом, суть работы автомата сводится к тому, чтобы прочитать очередной входной символ и, используя соответствующее правило перехода, перейти в другое состояние.

Связь между конечными автоматами и регулярными грамматиками самая непосредственная, что следует из утверждения:

Каждой грамматике можно поставить в соответствие эквивалентный ей автомат, и каждому автомату соответствует эквивалентная ему грамматика.

Итак, мы установили взаимосвязи между грамматиками, языками и автоматами: