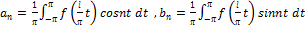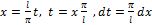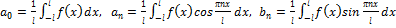Замена переменной в ТИ (геометрический вывод для общего случая); переход в ТИ к цилиндрическим и сферическим координатам.
а) переход к цилиндрическим координатам
 M(x,y,z)=M(ρcos(φ), ρsin(φ),z)
M(x,y,z)=M(ρcos(φ), ρsin(φ),z)  (2)
(2)
(x,y,z)↔(ρ, φ,z)
x= ρcos(φ)
 (1)
(1)  (1’)
(1’)
 (2)
(2)

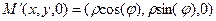
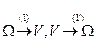
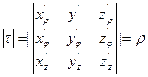 это знак якобиана если что;)
это знак якобиана если что;)
dV=dxdydz=  dρdφdz (3)
dρdφdz (3)

 (4)
(4)
б) Переход к сферическим координатам

ψ-отсчитывается от Oz по часовой стрелке

r-радиус-вектор точки M


Пусть  -новые координаты, тогда:
-новые координаты, тогда:
 (5)
(5) 

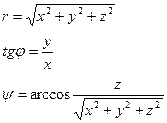 (5’)
(5’)
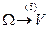
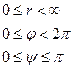


dxdydz= 
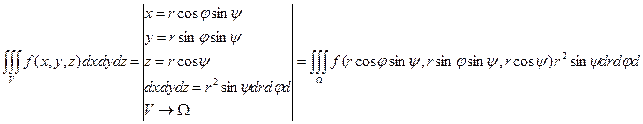
6.криволинейные интегралы: 1)пусть переменная t 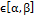 с помощью отображений x=x(t),y=y(t),z=z(t) отображает [
с помощью отображений x=x(t),y=y(t),z=z(t) отображает [ 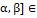 R’ в Г
R’ в Г 
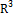 (1);2)
(1);2) 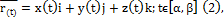 тогда x(t),y(t),z(t) – координаты вектор-функции (2) и определяет некоторую кривую в пространстве,т.е. x=x(t), y=y(t),z=z(t),t
тогда x(t),y(t),z(t) – координаты вектор-функции (2) и определяет некоторую кривую в пространстве,т.е. x=x(t), y=y(t),z=z(t),t 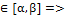 параметр.уравнение кривой в пространстве.Если t –время,то (3)-уравнение траектории движения.3)если
параметр.уравнение кривой в пространстве.Если t –время,то (3)-уравнение траектории движения.3)если  предшествует точке M(
предшествует точке M( , т.е. M[x(
, т.е. M[x( y(
y( ,z(
,z( ] предшествует M[x(
] предшествует M[x(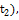 y(
y( ,z(
,z( ]. Г:
]. Г: 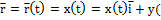 t)
t) 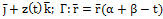 .если
.если 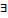
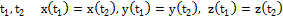 .если M(
.если M(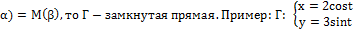 t
t  x(0)=x(2
x(0)=x(2 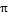 ),y(0)=y(2
),y(0)=y(2 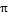 )=0.
)=0.
Криволинейные интегралы 2 рода
Определение: Конечный предел интегральной суммы In при λ→∞,не зависящий от точек Mi,называется криволинейным интегралом
второго рода от функций P,Q,R по пути L:
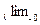 In=
In= 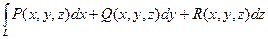
Определение (еще одно хз какое лучше): Если вдоль кривой L определены функции P(M) = P(x, y, z),
Q(M) = Q(x, y, z), R(M) = R(x, y, z) и существуют интегралы:  ,
, 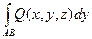 ,
, 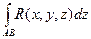 ,то и их сумму называют криволинейным интегралом второго рода (общего вида) и полагают:
,то и их сумму называют криволинейным интегралом второго рода (общего вида) и полагают:  =
=  +
+ 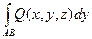 +
+ 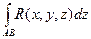 (1)
(1)
Свойства КИ-2:
1) Если функции P(M), Q(M), R(M) непрерывны на кривой (АВ), то интеграл (1) существует
2) При изменении направления кривой (то есть перемены местами начальной и конечной ее точек) криволинейный интеграл 2-го рода меняет знак:  = -
= - 
Про работу: Работа при перемещении тела в силовом поле 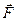 вдоль кривой C выражается через криволинейный интеграл второго рода:
вдоль кривой C выражается через криволинейный интеграл второго рода:
A=  , где
, где 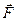 − сила, действующая на тело,
− сила, действующая на тело, 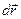 − единичный касательный вектор (рисунок 1). Обозначение
− единичный касательный вектор (рисунок 1). Обозначение 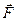 *
* 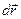 означает скалярное произведение векторов
означает скалярное произведение векторов 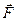 и
и 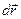 .
.
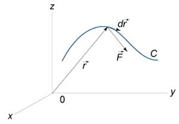
Механически КИ-2 представляет собой работу переменной силы 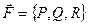 , точка приложения которой описывает кривую L
, точка приложения которой описывает кривую L
Вычисление КИ-2: Если линия AB задана в параметрической форме:x=x(t), y=y(t), z=z(t), t1≤t≤t2, где x(t), y(t), z(t) – непрерывно дифференцируемые функции, и при изменении параметра t от t1 к t2 кривая описывается именно от точки A к точке B, то
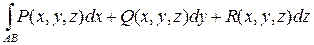 =
= 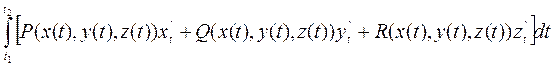
Причем КИ-2 существует, если существует определенный интеграл
Решение уравнения с разделяющимися переменными
Понятие однородной функции n -ого измерения однородные ДУ-1, их решение
Линейные ДУ-1: определение, отыскание общего решения методом Бернулли.
Линейные ДУ высшего порядка(ДУ- n): однородные, неоднородные. Однородные ДУ- n: доказать теоремы о свойствах решений, понятие фундаментальной системы ЛОДУ- n. Доказать теорему о структуре общего решения ЛОДУ- n.
 (1)
(1)


Если при всех рассматриваемых значениях x ф-я  то уравнение (1) наз-ся линейным однородным, в противном сл-е он наз-ся лин-но неоднородным.
то уравнение (1) наз-ся линейным однородным, в противном сл-е он наз-ся лин-но неоднородным.
Введем оператор: 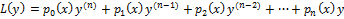 (2)
(2)
С помощью оператора (2) ур-е (1) примет вид: 
ЛОДУ-(n) Свойства решений 
Т1 Если  - решения, то
- решения, то  - тоже решения
- тоже решения
Д-во: 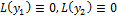
Тогда: 
Т2 Если 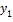 - решение, то
- решение, то 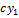 -тоже решение, где
-тоже решение, где 
Д-во: 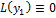 , тогда
, тогда

Понятие ФС ЛОДУ-(n)
Т  опред. на
опред. на  были лин-но незав-мы, необходимо и достаточно чтобы Вронскиан
были лин-но незав-мы, необходимо и достаточно чтобы Вронскиан 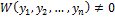 хотя бы в одной точке на
хотя бы в одной точке на 
Т Если Вронскиан 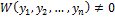 в точке
в точке  , то он не равен о ни в одной точке
, то он не равен о ни в одной точке 
О n - лин-но незав-х решений ЛОДУ-(n) наз-ся фундаментальной системой решений (ФСР)
Т о структуре общего решения ОЛДУ-(n)
Если  – ФСР ОЛДУ-(n)
– ФСР ОЛДУ-(n)
 , то общ. Решение ОЛДУ-(n) имеет вид:
, то общ. Решение ОЛДУ-(n) имеет вид:
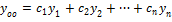 , (2)
, (2) 
Д-во: имеем 
А) Тогда 
Б) Покажем, что задача Коши имеет единственное решение:
 (3)
(3)
(2) в (3):  (4)
(4)
(4) – система лин-х неодн-х алгебр-х ур-й. Она имеет единственное решение, если опред-ль системы не равен 0.

Значит (4) – единственное решение 
Подставляя найденное значение 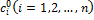 в (2) получаем решение задачи коши. Теор. Доказана
в (2) получаем решение задачи коши. Теор. Доказана
Вопрос.
П-ОЛДУ с постоянными коэффициентами
L(y)=yn+a1yn-1+…+an-1y’+any=0 (11)
a1,a2,…,an-const
Метод Эйлера: ищем решение в виде y=eλx λ-const (12)
y’=λeλx,y”=λ2eλx…yn=λneλx (13)
(12) и (13) в (11)
L(eλx)= λneλx+a1 λn-1eλx+…+an eλx
L(eλx)= (λn+a1 λn-1+a2 λn-2+…+an) eλx
L(eλx)=P(λ) eλx≡0 (14)
eλx≠0 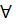 xϵ(-∞;∞)
xϵ(-∞;∞)
Из (14) следует P(λ)≡λn+a1 λn-1+…an=0 (15)
Характеристическое уравнение(ху)
Задача. Интегрирование диф. уравнения свелось в
Случаи:
1. ХУ(15) имеет n различных вещественных корней
n решений λ1, λ2,.., λn y1= eλ1x,y2= eλ2x,…,yn= eλx(16)

 W(eλ1X,…, eλnX)= eλ1X eλ2X … eλnX
W(eλ1X,…, eλnX)= eλ1X eλ2X … eλnX
λ1 eλ1X x2 eλ2X… λn eλnX
………………………
λ1n-1 eλ1X … λnn-1 eλnX

 = eλ1X* eλ2X*… eλnX * I I …. I
= eλ1X* eλ2X*… eλnX * I I …. I
λ1 λ2 …. λn ≠0 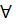 xϵ(-∞;∞)
xϵ(-∞;∞)
λ1n-1 λ2n-1… λnn-1
определитель Вандер Монда т.е (16)-ФСР
Тогда yоо=с1y1+ с2y2+…+ сnyn= c1eλ1X + c2 eλ2X+…+ cn eλnX (17)
2. Среди корней XУ имеется комплексный корень λ1=α+iβ
Тогда имеется обязательно сопряжённый корень λ2=α+iβ
y1= eα+iβ)x=eαx(cosβx+isinβx)= eαxcosβx+ ieαxsinβx=u(x)+iv(x)=y1(c волнистой чертой) y2(c волн.ч)= eα-iβ=eαxcosβx-ieαxsinβx= u(x)+iv(x)
Теорема о комплексном решении ДУ
Пусть y=u+iv – комплексное решение ДУ. Тогда L(y)≡0 следовательно L(u)+iL(v)=0 следовательно 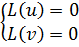
т.е u(x) и v(x)-действительное решение ДУ.
Вывод: двум комплексным сопряжённым корням λ1,2=α+iβ характеристического уравнения P(λ)=0 соответствует вещественное решение y1= eαxcosβx,y2= eαxsinβx
3. Среди корней ХУ корень λ1 кратности “к”
XУ P(λ)=(λ-λ1)kQn-k(λ)=0 (18)
 P’(λ)=k(λ- λ1)k-1 Q(λ)+ (λ- λ1)kQ’(λ)
P’(λ)=k(λ- λ1)k-1 Q(λ)+ (λ- λ1)kQ’(λ)
P’’(λ)= k(k-1)(λ-λ1)k-2Q(λ)+2k(λ-λ1)k-1Q’(λ)+ (λ-λ1)kQ’’(λ)
…………………………………………………………….. (19)
P(k) (λ)=k(k-1)…2*1Q(λ)+…+ (λ-λ1)kQk(λ)
Если λ1-корень ХУ(18), то (Q(λ1)≠0)
P(λ1)≡0 P’(λ1)=0,P’’(λ1)=0…,Pk-1(λ1),но Pk(λ1)=k’Q(λ1)≠0
Ранее имеем L(eλx)=P(λ) eλx=0 (20)
Продифференцируем соотношение (20) по λ:
(L(eλx))’λ=(P(λ) eλx)’λ ;(eλx)’=P’(λ) eλx+P(λ)x eλx
 L(x eλx)=P’(λ) eλx+P(λ)x eλx
L(x eλx)=P’(λ) eλx+P(λ)x eλx
Ещё раз дифференцируем по λ k-2 раз
L(x2 eλx)=P’’(λ) eλx+2P’(λ)x eλx+P(λ) eλxx2 (21)
Если в соотношении (21) подставим λ1-корень ХУ,то будем иметь
L(x eλx)=P’(λ1) eλ1x+P(λ1)x eλ1x=см 19=0 L(x eλ1x)≡0 следовательно x eλ1x тоже решение ОЛДУ-n. L(x2 eλ1x)=см 19=0+0+0=0 следовательно x2 eλ1x-тоже решение ОЛДУ-n. L(xk-1 eλ1x)=0+0+…+0=0 следовательно xk-1 eλ1x тоже решение ОЛДУ-n. Вывод: Если λ1-как кратный корень ХУ, то ему соответствует,,к,, решений:
y1= eλ1x,y2=x eλ1x,y3=x2 eλ1x,…,yk=xk-1 eλ1x –входят в ФСР как лин. независимые
4. Среди корней ХУ имеются почленно сопряжённые как кратные корни λ1,2=α+iβк р “ к” Всего 2к корней. Следует 2 кратным корнем имеет два вещественные решения y1= eαxcosβx,y2= eαxsinβx
В силу кратности y3=x eαxcosβx,…,y2k-1=xk-1 eαxcosβx
y4=x eαxsinβx,…, y2k=xk-1 eαxsinβx
Доказательство
(Sn) A= 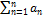
(Sn) B= 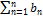
(Sn)A  (Sn)B
(Sn)B 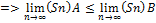 , SA
, SA 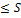 B (2)
B (2)
Из(2) 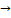 Если
Если  – сходится, то
– сходится, то 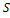 B -конечная => SA -конечная <
B -конечная => SA -конечная < 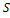 B =>
B => 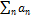 - сходится
- сходится
Из(2) 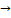 Если
Если 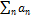 - – расходится, то SA -бесконечная =>
- – расходится, то SA -бесконечная => 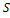 B -бесконечная > SA =>
B -бесконечная > SA =>  - расходится
- расходится
Признак Даламбера
Если в ряде 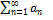 (an
(an 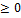 )
) 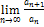 =L
=L
L<1-сходится
L>1 расходится
L=1 -??
Доказательство
a) L<1; 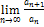 =L
=L
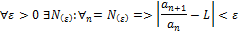
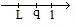 L<q<1
L<q<1
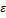 =q-L>0
=q-L>0
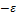 <
< 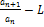 <
< 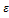 = q-L
= q-L
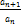 <q
<q
Начиная с 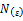
aN+1<q*aN
aN+2<q*aN+1<q2an
a1+a2+a3+…aN+aN+1+aN+2+… (4)
aN + q*aN+q2aN+q3aN+… (5)
начиная с номера 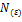 члены ряда (1)<(2)
члены ряда (1)<(2)
а ряд (2)-геометрическая прогрессия со знаменателем q>1
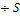 =
= 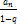 - кон.число по теореме сравнения в форме неравенства
- кон.число по теореме сравнения в форме неравенства
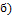 L>1;
L>1; 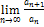 =L члены с каждого номера члены ряда возрастают an+1>an, т.е. не выполняется НУС
=L члены с каждого номера члены ряда возрастают an+1>an, т.е. не выполняется НУС
а значит ряд расходится
в) L=1-???
Коши-Радикальный
Если в 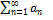 (an
(an 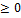 ),
), 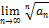 =L, то
=L, то
L<1-ряд сходится
L>1-ряд расходится
L=1-??
Доказательство
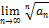 =L
=L 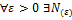
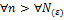 => |
=> | 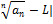 <
< 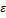
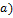 L <1
L <1
 =q-L
=q-L
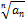 -L<
-L< 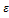 =q-L
=q-L
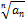 < qn начиная с некоторого номера
< qn начиная с некоторого номера 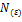
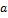 n <qn
n <qn
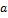 N <qN
N <qN
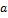 N+1 <qN+1
N+1 <qN+1
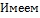 2 ряда
2 ряда
a1+a2+a3+…aN+aN+1+aN+2+… (6)
qN+qN+1+qN+2+… (7)
начиная с N члены (6)<(7) ряд (7) геом прогрессия 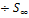 q<1;
q<1; 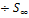 =
= 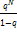 - конечное число, тогда по признаку сравнения (6) сходится
- конечное число, тогда по признаку сравнения (6) сходится
Б) L>1 aN+1>aN; aN>1 т.е не выполняется НУС
В) L=1-??
Признак Коши-Интегральный
Рассмотрим ряд 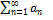 (an
(an 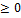 )
)
a(n) непрерывная функция на [n0; 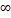 ]
]
Если 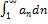 , - конечное число, то
, - конечное число, то 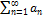 –сходится
–сходится
Если 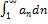 =0, или
=0, или 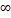 , то
, то  – расходится
– расходится
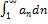 =A(n)
=A(n) 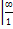 =
= 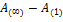
Вопрос 20. Если для последовательности {Sn,n≥1} частичных сумм существует конечны предел S, то ряд называется сходящимся, а число S-суммой данного ряда. Ряд называется расходящимся, если lim Sn (при n→0) не существует или бесконечен.
НУС Для того что бы ΣAn сходился, необходимо, что бы lim An(при n→0)=0
Если ряд сходится то остаток ряда тоже сходиться. Отбрасывание первых членов ряда не влияют на сходимость. Если ряд сходиться то остаток стремиться к нулю.
Т Знакоположительный ряд всегда имеет сумму: А) Если сумма ряда конечна, то ряд сходиться. Б) Если сумма бесконечна, то ряд разходится.
Абсолютная и условная сходимость Ряд ΣA (от 1 до ∞) называется абсолютно сходящимся, если ряд Σ‖A‖ также сходится.
Если ряд ΣAn (от 1 до ∞) сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно.
Ряд ΣА (от 1 до ∞) называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
Функциональные ряды.
О) ФР: 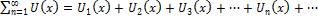 (1) x Î<a,b> (1)
(1) x Î<a,b> (1)
O) Если в (1) x=x0, то 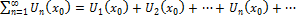 (2) – числовой ряд
(2) – числовой ряд
О) Если 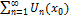 – (2) сходится, то говорят, что ФР (1) сходится в (.) x0
– (2) сходится, то говорят, что ФР (1) сходится в (.) x0
О) Если 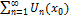 – (2) " x0 Î <a,b>, то говорят, что ФР (1) сходится на <a,b>
– (2) " x0 Î <a,b>, то говорят, что ФР (1) сходится на <a,b>
О) Если 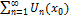 - (2) расходится, то ФР (1) расходится в (.) x0
- (2) расходится, то ФР (1) расходится в (.) x0
О) 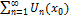 - (2) сходится в (.) x0, если
- (2) сходится в (.) x0, если 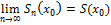
Частичная сумма сумма числового ряда
т.е. " e>0 $ N(e,x0): "(n>N) Þ ½Sn(x0)-S(x0)½<e
!!! N(e,x0) зависит и от e и от x0
Равномерная сходимость.
О) ФР (1) сходится равномерно на <a,b>, если " e>0 $ N(e): "(n>N) Þ ½Sn(x)-S(x)½<e " “x” Î <a,b> одновременно, где Sn(x)= 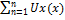 – частичная сумма, S(x) – сумма ряда
– частичная сумма, S(x) – сумма ряда
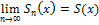
S(x)=Sn(x)+Rn(x)
Rn(x)=Un+1(x)+Un+2(x)+… - остаток ряда
Вопрос
PU y(x)= 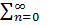 y(0)n/n!*xn xϵ<-R,R> (1)
y(0)n/n!*xn xϵ<-R,R> (1)
PT y(x)=  y(0)n/n!*(x-x0) xϵ<-R,R> (2)
y(0)n/n!*(x-x0) xϵ<-R,R> (2)
1. Вычисление значений функций y(x) x=x1. Раскладываем функцию в ряд Тейлора и Маклорена и вычисляем значение функции
2. Вычисление интегралов. 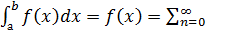 fn(x0)/n!(x-x0)n=
fn(x0)/n!(x-x0)n= 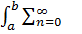 fn(x0)/n! (x-x0)ndx=
fn(x0)/n! (x-x0)ndx= 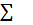 fn(x0)/n!
fn(x0)/n! 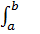 (x-x0)ndx=
(x-x0)ndx=
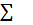 f(x0)(x-x0)n+1/n!(n+1)
f(x0)(x-x0)n+1/n!(n+1)  [a,b]
[a,b] 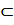 <-R,R>
<-R,R>
3. ДУ. a) Линейные ДУ. y’’+p(x)y’+g(x)y=0 Пусть p(x)= 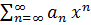
q(x)=  ; y(x)=
; y(x)= 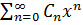 (3) Подставим (3) в и находим коэффициенты Сn и находим из обращения в нуль коэффициентов при любой степени х в полученном выражении
(3) Подставим (3) в и находим коэффициенты Сn и находим из обращения в нуль коэффициентов при любой степени х в полученном выражении
б) Если p(x)= 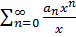 ; q(x)=
; q(x)= 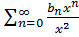 Пусть a0,b0,b1 не равны, о оновр тогда решение уравнения (1) можно искать в виде обобщённого степенного ряда y(x)=xs
Пусть a0,b0,b1 не равны, о оновр тогда решение уравнения (1) можно искать в виде обобщённого степенного ряда y(x)=xs 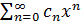 ; ρ(ρ-1)+a0ρ+b0=0 (6)
; ρ(ρ-1)+a0ρ+b0=0 (6)
a0= 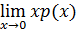 ,b0=
,b0= 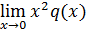
a) Если ρ1-ρ2- не целое. y1(x)=xρ1 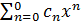 ; y2(x)=xρ2
; y2(x)=xρ2 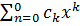
y00=c1y1(x)+c2xy2(x) (!!!)
б) Если ρ1-ρ2- целое
2.1 Ряд Фурье. Пространство функции L 2 [- 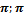 ]. Определение, св-ва.
]. Определение, св-ва.
Рассмотрим множество f(x):  =
= 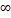 непрерывные на [-
непрерывные на [-  ]
]
Кусочные непрерывные [-  ], имеющие кон число точек разрыва 1го рода
], имеющие кон число точек разрыва 1го рода
Свойства функции:
1) Если f(x)  L2, то С*f(x)
L2, то С*f(x)  L2
L2
Доказательство: 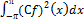 =С2*
=С2*  <
< 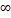
2) Если f1(x);f2(x)  L2 то f1(x)+f2(x)
L2 то f1(x)+f2(x)  L2
L2
Д-во: ( f1(x)+f2(x))2 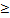 0
0
f12  f1f2+f22
f1f2+f22 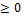 => f12+f22>
=> f12+f22>  f1f2
f1f2
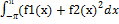 =
= 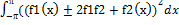 <
< 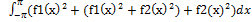 <2
<2 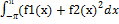
Благодаря этим свойствам образуется линейное векторное пространство, которым можно показать, что L2 не имеет конечного базиса. Базис содержит бесконечное множество векторов
Можно ввести скалярное произведение:
{f(x),g(x)} = 
1) (g(x), f(x)) = 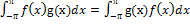
(f(x),g(x)) =(g(x),f(x))
2) {f1(x)+f2(x),g(x)} = 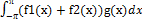 =
= 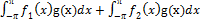
(  +
+ 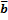 )*
)* 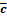 =
=  *
* 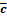 +
+ 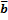 *
* 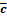
3) { f(x), f(x)} = 
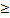 0
0
4) (|f(x)|) = 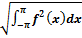
5) {|f(x)-g(x)|}= 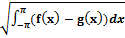
2(Ряды Фурье). Показать ортогональность функций 1, cosx, sinx, cos2x, sin2x,…,cosnx, sinnx,… на [- π, π ].
{1, sinx, cosx, sin 2x, cos 2x,..., sin nx, cos nx,...}
1. 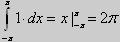 Поэтому
Поэтому 
2. 
3. 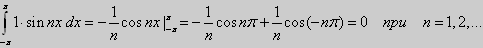
4. 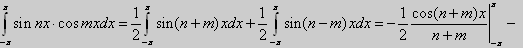
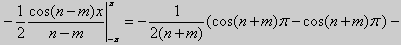
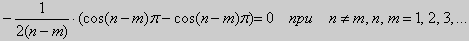
Если n=m, то 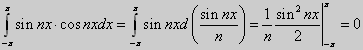
5. 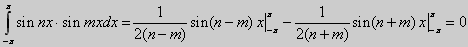
при n ≠ m, n, m = 1, 2, 3,... Если n = m, то 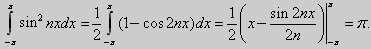
Значит, 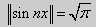
6. 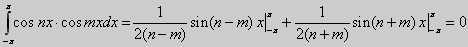
при n ≠ m, n, m = 1, 2, 3,... Если n = m, то 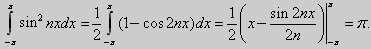
То есть 
Таким образом, доказано, что система на отрезке [ - π, + π] ортогональная.
Вопрос 3 фурье

5)Ряд Фурье для периодических функций с периодом T=2l
Пусть f(x) есть период. ф-я с T=2l,отличным от 2π. Разложим ее в ряд Фурье. Замена переменной: 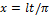 /
/
Тогда ф-я  будет переод-й ф-й от t c T=2π. Ее можно разложить на
будет переод-й ф-й от t c T=2π. Ее можно разложить на 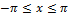
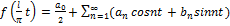 ,где
,где 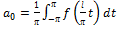 ,
, 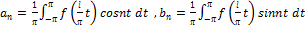
Возвратимся к старой переменной: 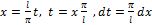
Имеем: 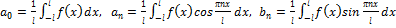
Ряд Фурье будет иметь вид: 
Замена переменной в ТИ (геометрический вывод для общего случая); переход в ТИ к цилиндрическим и сферическим координатам.
а) переход к цилиндрическим координатам
 M(x,y,z)=M(ρcos(φ), ρsin(φ),z)
M(x,y,z)=M(ρcos(φ), ρsin(φ),z)  (2)
(2)
(x,y,z)↔(ρ, φ,z)
x= ρcos(φ)
 (1)
(1)  (1’)
(1’)
 (2)
(2)

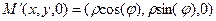
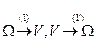
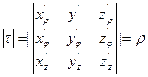 это знак якобиана если что;)
это знак якобиана если что;)
dV=dxdydz=  dρdφdz (3)
dρdφdz (3)

 (4)
(4)
б) Переход к сферическим координатам

ψ-отсчитывается от Oz по часовой стрелке

r-радиус-вектор точки M


Пусть  -новые координаты, тогда:
-новые координаты, тогда:
 (5)
(5) 

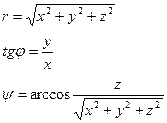 (5’)
(5’)
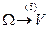
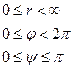


dxdydz= 
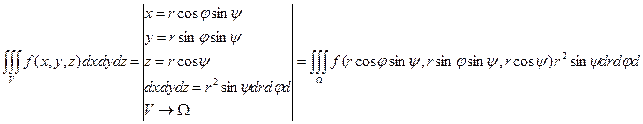
6.криволинейные интегралы: 1)пусть переменная t 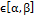 с помощью отображений x=x(t),y=y(t),z=z(t) отображает [
с помощью отображений x=x(t),y=y(t),z=z(t) отображает [ 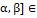 R’ в Г
R’ в Г 
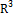 (1);2)
(1);2) 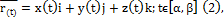 тогда x(t),y(t),z(t) – координаты вектор-функции (2) и определяет некоторую кривую в пространстве,т.е. x=x(t), y=y(t),z=z(t),t
тогда x(t),y(t),z(t) – координаты вектор-функции (2) и определяет некоторую кривую в пространстве,т.е. x=x(t), y=y(t),z=z(t),t 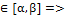 параметр.уравнение кривой в пространстве.Если t –время,то (3)-уравнение траектории движения.3)если
параметр.уравнение кривой в пространстве.Если t –время,то (3)-уравнение траектории движения.3)если  предшествует точке M(
предшествует точке M( , т.е. M[x(
, т.е. M[x( y(
y( ,z(
,z( ] предшествует M[x(
] предшествует M[x(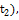 y(
y( ,z(
,z( ]. Г:
]. Г: 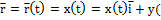 t)
t) 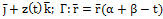 .если
.если 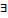
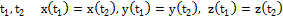 .если M(
.если M(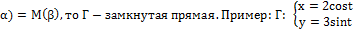 t
t  x(0)=x(2
x(0)=x(2 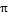 ),y(0)=y(2
),y(0)=y(2 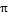 )=0.
)=0.



 M(x,y,z)=M(ρcos(φ), ρsin(φ),z)
M(x,y,z)=M(ρcos(φ), ρsin(φ),z)  (2)
(2) (1)
(1)  (1’)
(1’)
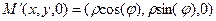
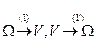
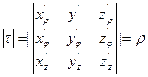 это знак якобиана если что;)
это знак якобиана если что;) dρdφdz (3)
dρdφdz (3)
 (4)
(4)



 -новые координаты, тогда:
-новые координаты, тогда: (5)
(5) 

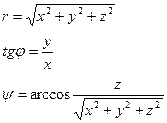 (5’)
(5’)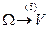
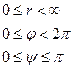



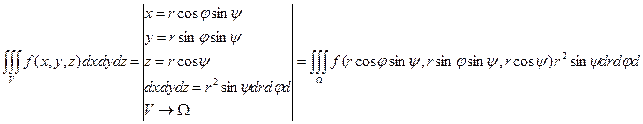
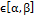 с помощью отображений x=x(t),y=y(t),z=z(t) отображает [
с помощью отображений x=x(t),y=y(t),z=z(t) отображает [ 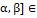 R’ в Г
R’ в Г 
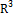 (1);2)
(1);2) 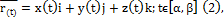 тогда x(t),y(t),z(t) – координаты вектор-функции (2) и определяет некоторую кривую в пространстве,т.е. x=x(t), y=y(t),z=z(t),t
тогда x(t),y(t),z(t) – координаты вектор-функции (2) и определяет некоторую кривую в пространстве,т.е. x=x(t), y=y(t),z=z(t),t 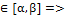 параметр.уравнение кривой в пространстве.Если t –время,то (3)-уравнение траектории движения.3)если
параметр.уравнение кривой в пространстве.Если t –время,то (3)-уравнение траектории движения.3)если  предшествует точке M(
предшествует точке M( , т.е. M[x(
, т.е. M[x( y(
y( ,z(
,z(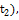 y(
y(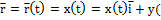 t)
t) 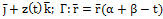 .если
.если 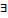
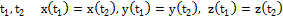 .если M(
.если M(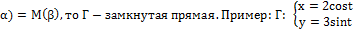 t
t  x(0)=x(2
x(0)=x(2 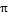 ),y(0)=y(2
),y(0)=y(2 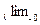 In=
In= 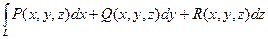
 ,
, 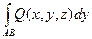 ,
, 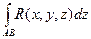 ,то и их сумму называют криволинейным интегралом второго рода (общего вида) и полагают:
,то и их сумму называют криволинейным интегралом второго рода (общего вида) и полагают:  =
=  +
+ 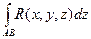 (1)
(1) = -
= - 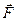 вдоль кривой C выражается через криволинейный интеграл второго рода:
вдоль кривой C выражается через криволинейный интеграл второго рода: , где
, где 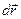 − единичный касательный вектор (рисунок 1). Обозначение
− единичный касательный вектор (рисунок 1). Обозначение 
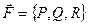 , точка приложения которой описывает кривую L
, точка приложения которой описывает кривую L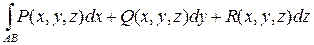 =
= 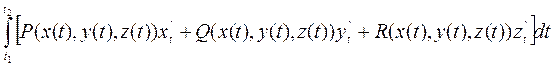
 (1)
(1)

 то уравнение (1) наз-ся линейным однородным, в противном сл-е он наз-ся лин-но неоднородным.
то уравнение (1) наз-ся линейным однородным, в противном сл-е он наз-ся лин-но неоднородным.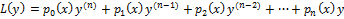 (2)
(2)

 - решения, то
- решения, то  - тоже решения
- тоже решения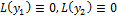

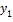 - решение, то
- решение, то 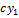 -тоже решение, где
-тоже решение, где 
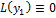 , тогда
, тогда
 опред. на
опред. на  были лин-но незав-мы, необходимо и достаточно чтобы Вронскиан
были лин-но незав-мы, необходимо и достаточно чтобы Вронскиан 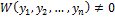 хотя бы в одной точке на
хотя бы в одной точке на  , то он не равен о ни в одной точке
, то он не равен о ни в одной точке  , то общ. Решение ОЛДУ-(n) имеет вид:
, то общ. Решение ОЛДУ-(n) имеет вид: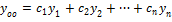 , (2)
, (2) 


 (3)
(3) (4)
(4)

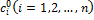 в (2) получаем решение задачи коши. Теор. Доказана
в (2) получаем решение задачи коши. Теор. Доказана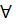 xϵ(-∞;∞)
xϵ(-∞;∞)
 W(eλ1X,…, eλnX)= eλ1X eλ2X … eλnX
W(eλ1X,…, eλnX)= eλ1X eλ2X … eλnX
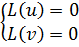
 P’(λ)=k(λ- λ1)k-1 Q(λ)+ (λ- λ1)kQ’(λ)
P’(λ)=k(λ- λ1)k-1 Q(λ)+ (λ- λ1)kQ’(λ) L(x eλx)=P’(λ) eλx+P(λ)x eλx
L(x eλx)=P’(λ) eλx+P(λ)x eλx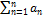
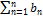
 (Sn)B
(Sn)B 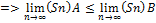 , SA
, SA 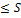 B (2)
B (2)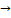 Если
Если  – сходится, то
– сходится, то 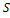 B -конечная => SA -конечная <
B -конечная => SA -конечная < 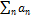 - сходится
- сходится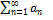 (an
(an 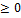 )
) 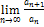 =L
=L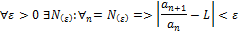
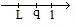 L<q<1
L<q<1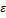 =q-L>0
=q-L>0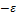 <
< 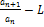 <
< 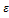 = q-L
= q-L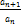 <q
<q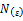
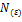 члены ряда (1)<(2)
члены ряда (1)<(2)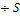 =
= 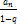 - кон.число по теореме сравнения в форме неравенства
- кон.число по теореме сравнения в форме неравенства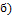 L>1;
L>1; 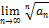 =L, то
=L, то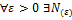
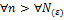 => |
=> | 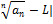 <
< 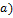 L <1
L <1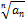 -L<
-L< 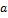 n <qn
n <qn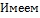 2 ряда
2 ряда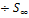 q<1;
q<1; 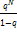 - конечное число, тогда по признаку сравнения (6) сходится
- конечное число, тогда по признаку сравнения (6) сходится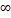 ]
]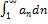 , - конечное число, то
, - конечное число, то 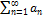 –сходится
–сходится – расходится
– расходится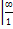 =
= 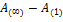
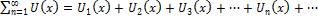 (1) x Î<a,b> (1)
(1) x Î<a,b> (1)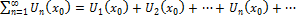 (2) – числовой ряд
(2) – числовой ряд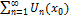 – (2) сходится, то говорят, что ФР (1) сходится в (.) x0
– (2) сходится, то говорят, что ФР (1) сходится в (.) x0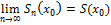
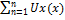 – частичная сумма, S(x) – сумма ряда
– частичная сумма, S(x) – сумма ряда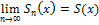
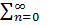 y(0)n/n!*xn xϵ<-R,R> (1)
y(0)n/n!*xn xϵ<-R,R> (1) y(0)n/n!*(x-x0) xϵ<-R,R> (2)
y(0)n/n!*(x-x0) xϵ<-R,R> (2)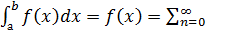 fn(x0)/n!(x-x0)n=
fn(x0)/n!(x-x0)n= 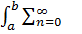 fn(x0)/n! (x-x0)ndx=
fn(x0)/n! (x-x0)ndx= 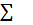 fn(x0)/n!
fn(x0)/n! 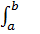 (x-x0)ndx=
(x-x0)ndx= [a,b]
[a,b] 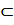 <-R,R>
<-R,R>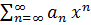
 ; y(x)=
; y(x)= 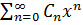 (3) Подставим (3) в и находим коэффициенты Сn и находим из обращения в нуль коэффициентов при любой степени х в полученном выражении
(3) Подставим (3) в и находим коэффициенты Сn и находим из обращения в нуль коэффициентов при любой степени х в полученном выражении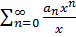 ; q(x)=
; q(x)= 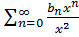 Пусть a0,b0,b1 не равны, о оновр тогда решение уравнения (1) можно искать в виде обобщённого степенного ряда y(x)=xs
Пусть a0,b0,b1 не равны, о оновр тогда решение уравнения (1) можно искать в виде обобщённого степенного ряда y(x)=xs 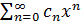 ; ρ(ρ-1)+a0ρ+b0=0 (6)
; ρ(ρ-1)+a0ρ+b0=0 (6)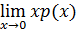 ,b0=
,b0= 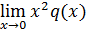
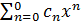 ; y2(x)=xρ2
; y2(x)=xρ2 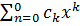
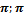 ]. Определение, св-ва.
]. Определение, св-ва. =
=  ]
] L2, то С*f(x)
L2, то С*f(x) 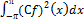 =С2*
=С2* 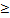 0
0 f1f2+f22
f1f2+f22 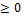 => f12+f22>
=> f12+f22> 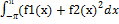 =
= 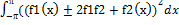 <
< 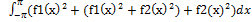 <2
<2 
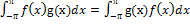
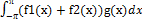 =
= 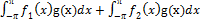
 +
+ 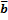 )*
)* 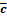 =
= 
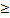 0
0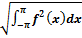
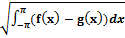
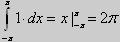 Поэтому
Поэтому 

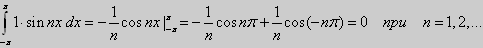
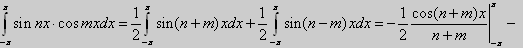
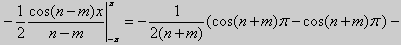
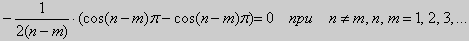
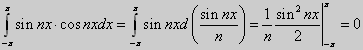
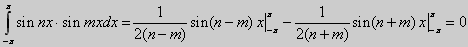
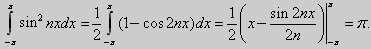
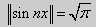
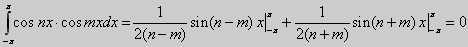


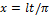 /
/ будет переод-й ф-й от t c T=2π. Ее можно разложить на
будет переод-й ф-й от t c T=2π. Ее можно разложить на 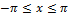
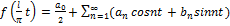 ,где
,где 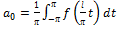 ,
,