Метод пассивного поиска
Возьмем число h>0 (шаг поиска), такое, что  , где k > 1 - целое число. Будем вычислять значение функции
, где k > 1 - целое число. Будем вычислять значение функции 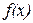 по формуле:
по формуле:
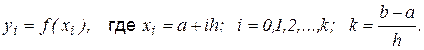 (2.2)
(2.2)
Из полученных значений выберем наименьшее:
 . (2.3)
. (2.3)
Тогда по критериям 1 и 2 можно утверждать, что точка  локального минимума находится на отрезке
локального минимума находится на отрезке  , где
, где
 . (2.4)
. (2.4)
Таким образом, минимум локализуется на промежутке длины не более 2 h и точка  – наилучшее приближение локального минимума среди всех
– наилучшее приближение локального минимума среди всех 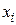 на
на  . (При необходимости можно продолжить локализацию функции
. (При необходимости можно продолжить локализацию функции 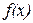 на отрезке
на отрезке  с шагом h 1 < h).
с шагом h 1 < h).
Пример поиска локального минимума функции методом пассивного поиска
Для функции  на отрезке
на отрезке  проведем пассивный поиск с шагом h = 1. Для этого по формуле (2.2) составим таблицу значений данной функции (табл. 2.1) с погрешностью 0.01 и построим ее график (рис.2.3).
проведем пассивный поиск с шагом h = 1. Для этого по формуле (2.2) составим таблицу значений данной функции (табл. 2.1) с погрешностью 0.01 и построим ее график (рис.2.3).
Таблица 2.1.

| - 5
| - 4
| - 3
| - 2
| - 1
| 0
| 1
| 2
| 3
| 4
| 5
|
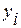
| 28.41
| -5.40
| -3.91
| 1.40
| 2.72
| 1.0
| 0.37
| 6.14
| 24.05
| 60.02
| 120.01
|
Из таблицы и графика (рис.2.3) видно, что на отрезке

, на интервалах (–
5. –3) и (
0. 2) имеются две точки локального минимума:

и
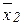
и соответствующие им локализующие тройки: {–
5, –4, –3 } и {
0, 1, 2 }, но абсолютный минимум достигается только в одной из них – при

= –
4.
В качестве подтверждения сказанному, проведем традиционный математический анализ данной функции по условиям (1.8), (1.9). Для этого вычислим первую и вторую производные функции 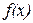 в окрестности точки
в окрестности точки 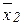 :
:  . Так как
. Так как  , а
, а  и
и  при всех x>0 (выполнено условие (1.9)), то на (0. 2) уравнение
при всех x>0 (выполнено условие (1.9)), то на (0. 2) уравнение 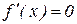 имеет единственное решение
имеет единственное решение 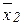 (стационарную точку функции по (1.8)), которая и является точкой минимума на
(стационарную точку функции по (1.8)), которая и является точкой минимума на 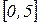 . Аналогичные вычисления в окрестности точки
. Аналогичные вычисления в окрестности точки  определят единственное решение на (– 5. –3). Поскольку на (– 3, 0) будет определена точка максимума
определят единственное решение на (– 5. –3). Поскольку на (– 3, 0) будет определена точка максимума  ,то точка
,то точка  является точкой минимума и на
является точкой минимума и на  . А так как других точек минимума на
. А так как других точек минимума на  нет, то, исходя из того, что
нет, то, исходя из того, что 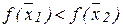 , можно сделать вывод - в точке
, можно сделать вывод - в точке  достигается глобальный минимум функции
достигается глобальный минимум функции  на отрезке
на отрезке 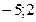 .
.
Пример поиска локального минимума методом деления отрезка пополам
Применяя классический и модифицированные алгоритмы, определим с точностью  точку
точку  локального минимума функции
локального минимума функции 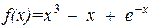 . Поиск будем производить на отрезке локализации
. Поиск будем производить на отрезке локализации  .
.
Согласно схемам 2.1. и 2.2 установим 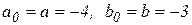 .
.
Классический алгоритм (схема 2.1).
Первая итерация:
1) вычислим  ,
, 
 ,
, 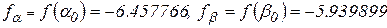 ;/
;/
2) сравним  и
и  . Так как
. Так как 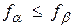 , то установим в качестве нового отрезка локализации отрезок
, то установим в качестве нового отрезка локализации отрезок  ;
;
3) и так как условия 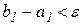 и
и  не выполняются, то произведем очередную итерацию.
не выполняются, то произведем очередную итерацию.
Итерационный процесс будем продолжать до тех пор, пока для установленного вновь отрезка локализации данные условия не будут выполнены. Результаты итераций сведем в таблицу 2.2.
Таблица 2.2
| № шага k
| 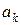
| 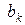
| 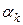
| 
| 
| 
| 
|
| 0
| -4.000000
| -3.000000
| -3.600000
| -3.400000
| -6.457766
| -5.939899
| 1.000000
|
| 1
| -4.000000
| -3.400000
| -3.760000
| -3.640000
| -6.448950
| -6.496707
| 0.600000
|
| 2
| -3.760000
| -3.400000
| -3.616000
| -3.544000
| -6.476333
| -6.363350
| 0.360000
|
| 3
| -3.760000
| -3.544000
| -3.673600
| -3.630400
| -6.509402
| -6.489656
| 0.216000
|
| 4
| -3.760000
| -3.630400
| -3.708160
| -3.682240
| -6.502006
| -6.509551
| 0.129600
|
| 5
| -3.708160
| -3.630400
| -3.677056
| -3.661504
| -6.509618
| -6.507023
| 0.077760
|
| 6
| -3.708160
| -3.661504
| -3.689497
| -3.680166
| -6.508658
| -6.509634
| 0.046656
|
| 7
| -3.689497
| -3.661504
| -3.678300
| -3.672701
| -6.509645
| -6.509312
| 0.027994
|
| 8
| -3.689497
| -3.672701
| -3.682779
| -3.679420
| -6.509517
| -6.509646
| 0.016796
|
| 9
| -3.682779
| -3.672701
| -3.678748
| -3.676732
| -6.509648
| -6.509607
| 0.010078
|
| 10
| -3.682779
| -3.676732
| -3.680360
| -3.679151
| -6.509630
| -6.509648
| 0.006047
|
| 11
| -3.680360
| -3.676732
| -3.678909
| -3.678183
| -6.509648
| -6.509644
| 0.003628
|
| 12
| -3.680360
| -3.678183
| -3.679489
| -3.679054
| -6.509645
| -6.509648
| 0.002177
|
| 13
| -3.679489
| -3.678183
| -3.678967
| -3.678706
| -6.509648
| -6.509648
| 0.001306
|
| 14
| -3.679489
| -3.678706
| -3.679176
| -3.679019
| -6.509648
| -6.509648
| 0.000784
|
Из таблицы видно, что искомый результат на 14-ом шаге вычислений. При этом: 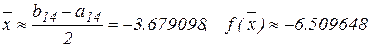 .
.
Метод золотого сечения
Отличие метода золотого сечения от метода деления отрезка пополам заключается в специальном разбиении отрезка локализации относительно его центра точками.
Термин «золотое сечение» ввел Леонардо да Винчи. Принципы, заложенные в основу этого сечения, широко использовались при композиционном построении многих произведений искусства античности и эпохи Возрождения: особенно в живописи и архитектуре.
Определение 2.1. Золотым сечением отрезка  называется такое разбиение отрезка на две неравные части точками
называется такое разбиение отрезка на две неравные части точками  и
и  , что отношение длины всего отрезка
, что отношение длины всего отрезка 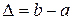 к длине его большей части
к длине его большей части  равно отношению длины большей части к длине
равно отношению длины большей части к длине  меньшей части:
меньшей части:  . При этом (рис.2.5) точки
. При этом (рис.2.5) точки 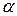 и
и  располагаются симметрично относительно центра отрезка
располагаются симметрично относительно центра отрезка  и могут быть определены с помощью следующих соотношений:
и могут быть определены с помощью следующих соотношений:
 .
.
Замечательно также, что точки  и
и  осуществляют золотое сечение не только всего отрезка
осуществляют золотое сечение не только всего отрезка  , но и соответственно подотрезков
, но и соответственно подотрезков  и
и  .
.






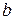
· · · ·


Рис.2.5. Выбор точек разбиения отрезка в методе золотого сечения
Итерационный процесс локализации минимума функции на заданном числовом отрезке в данном методе ведется аналогично локализации минимума функции в методе деления отрезка пополам. В отличие от него точки  и
и  на очередном шаге итерации находятся по формулам:
на очередном шаге итерации находятся по формулам:
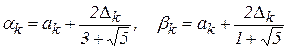 .
.
Свойства золотого сечения позволяют также несколько упростить процедуру поиска точки локализации  на очередном шаге вычислений. Действительно, какой бы из отрезков
на очередном шаге вычислений. Действительно, какой бы из отрезков  или
или  не был бы выбран за очередной отрезок локализации, точка
не был бы выбран за очередной отрезок локализации, точка  (
( , если
, если  и
и  , если
, если  ) совпадет с одной из точек
) совпадет с одной из точек 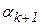 или
или  (рис 2.6). Поэтому на очередном шаге достаточно вычислить значение функции лишь в одной недостающей точке.
(рис 2.6). Поэтому на очередном шаге достаточно вычислить значение функции лишь в одной недостающей точке.



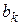
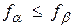

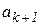
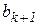
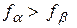
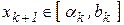
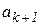
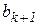
Рис.2.6. Графическая интерпретация метода золотого сечения
Пример поиска локального минимума методом золотого сечения
Применяя метод золотого сечения, определить с точностью 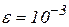 точку
точку 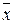 локального минимума функции
локального минимума функции  на отрезке локализации
на отрезке локализации  .
.
Так как данный метод отличается от метода деления отрезка пополам только способом выбора точек сужения отрезка локализации, то и алгоритм поиска решения, и программу реализации данного метода легко получить, сделав незначительные изменения в схеме 2.1 и программе, рассмотренных в п. 2.2. Для этого: в блоке 2 (сх.2.2) достаточно не вычислять величину 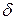 ; вместо вычислений
; вместо вычислений  и
и 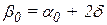 установить соответственно
установить соответственно 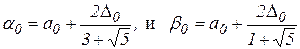 ; добавить вычисление величины
; добавить вычисление величины  .
.
Тогда, установив 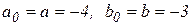 имеем:
имеем:
Первая итерация:
1) вычислим 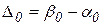 ,
, 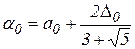 ,
,  и определим значения
и определим значения 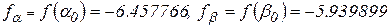 ;
;
2) сравним  и
и  . Так как
. Так как 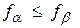 , то установим в качестве нового отрезка локализации отрезок
, то установим в качестве нового отрезка локализации отрезок 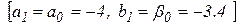 ;
;
3) и так как условия 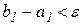 и
и  не выполняются, то произведем очередную итерацию.
не выполняются, то произведем очередную итерацию.
Итерационный процесс будем продолжать до тех пор, пока для установленного вновь отрезка локализации данные условия не будут выполнены. Результаты итераций сведем в таблицу 2.2.
Таблица 2.2
| № шага k
| 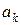
| 
| 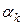
| 
| 
| 
| 
|
| 0
| -4.000000
| -3.000000
| -3.600000
| -3.400000
| -6.457766
| -5.939899
| 1.000000
|
| 1
| -4.000000
| -3.400000
| -3.760000
| -3.640000
| -6.448950
| -6.496707
| 0.600000
|
| 2
| -3.760000
| -3.400000
| -3.616000
| -3.544000
| -6.476333
| -6.363350
| 0.360000
|
| 3
| -3.760000
| -3.544000
| -3.673600
| -3.630400
| -6.509402
| -6.489656
| 0.216000
|
| 4
| -3.760000
| -3.630400
| -3.708160
| -3.682240
| -6.502006
| -6.509551
| 0.129600
|
| 5
| -3.708160
| -3.630400
| -3.677056
| -3.661504
| -6.509618
| -6.507023
| 0.077760
|
| 6
| -3.708160
| -3.661504
| -3.689497
| -3.680166
| -6.508658
| -6.509634
| 0.046656
|
| 7
| -3.689497
| -3.661504
| -3.678300
| -3.672701
| -6.509645
| -6.509312
| 0.027994
|
| 8
| -3.689497
| -3.672701
| -3.682779
| -3.679420
| -6.509517
| -6.509646
| 0.016796
|
| 9
| -3.682779
| -3.672701
| -3.678748
| -3.676732
| -6.509648
| -6.509607
| 0.010078
|
| 10
| -3.682779
| -3.676732
| -3.680360
| -3.679151
| -6.509630
| -6.509648
| 0.006047
|
| 11
| -3.680360
| -3.676732
| -3.678909
| -3.678183
| -6.509648
| -6.509644
| 0.003628
|
| 12
| -3.680360
| -3.678183
| -3.679489
| -3.679054
| -6.509645
| -6.509648
| 0.002177
|
| 13
| -3.679489
| -3.678183
| -3.678967
| -3.678706
| -6.509648
| -6.509648
| 0.001306
|
| 14
| -3.679489
| -3.678706
| -3.679176
| -3.679019
| -6.509648
| -6.509648
| 0.000784
|
Из таблицы видно, что искомый результат на 14-ом шаге вычислений. При этом:  .
.
Метод парабол
Существует множество методов локализации экстремума гладкой функции. Некоторые из них, например метод бисекции и метод Ньютона требуют вычисления производных. Такие методы достаточно эффективны, но не очень удобны для программной реализации, так как именно проблема вычисления производных является трудоемкой в ЭВМ-реализации. Предлагаемый метод не требует вычисления производных и, как мы убедимся ниже, является достаточно эффективным в случае удачной предварительной его настройки.
Предположим, что уже известны три предыдущих приближения к точке  – локального минимума функции
– локального минимума функции 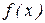 , т.е. получена локализующая тройка
, т.е. получена локализующая тройка  В качестве такой тройки можно воспользоваться, например, вычислениями, полученными на трех последних шагах (
В качестве такой тройки можно воспользоваться, например, вычислениями, полученными на трех последних шагах (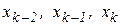 ) методом пассивного поиска. При этом соответствие между
) методом пассивного поиска. При этом соответствие между  и
и 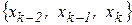 нужно установить так, чтобы выполнялось условие критерия 2:
нужно установить так, чтобы выполнялось условие критерия 2: 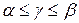 . Вложенная в
. Вложенная в 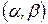 новая локализующая тройка строится при помощи интерполяционного полинома Ньютона
новая локализующая тройка строится при помощи интерполяционного полинома Ньютона 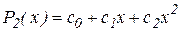 . График полинома
. График полинома 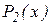 является параболой (рис.2.5.1), проходящей через три точки плоскости с координатами
является параболой (рис.2.5.1), проходящей через три точки плоскости с координатами  . Точка минимума
. Точка минимума  полинома
полинома 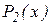 лежит в
лежит в  . Вычислив
. Вычислив 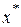 и
и 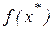 , сравним значение
, сравним значение 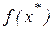 со значением
со значением 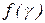 и по критерию 2 найдем новую локализирующую тройку.
и по критерию 2 найдем новую локализирующую тройку.
Полином 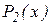 удобно представить в форме Ньютона с разделенными разностями:
удобно представить в форме Ньютона с разделенными разностями:
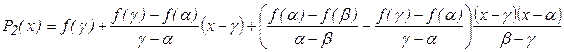 (13)
(13)
 y
y
y= 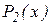
y= 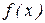
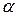
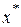
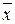
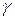
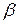 x
x
Рис.2.8. К методу парабол
В формуле (13) коэффициенты при неизвестных полинома 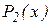 представлены формулами:
представлены формулами:
 ;
;
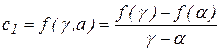 ;
;
 .
.
Сделав соответствующие приведения в терминах разделенных разностей, точку 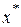 можно определить, воспользовавшись одной из формул:
можно определить, воспользовавшись одной из формул:
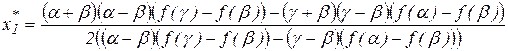 , (14)
, (14)
или
 , (15)
, (15)
или
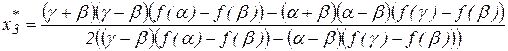 . (16)
. (16)
Выбор точки  следует сделать по тому представлению, которое будет вычисляться с меньшей потерей точности (значащих цифр в разностях). Однако, такой выбор на ЭВМ осуществить достаточно трудоемко. Поэтому, для определения конкретной точки
следует сделать по тому представлению, которое будет вычисляться с меньшей потерей точности (значащих цифр в разностях). Однако, такой выбор на ЭВМ осуществить достаточно трудоемко. Поэтому, для определения конкретной точки 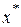 в ЭВМ-реализации можно принять условие: выбрать ту точку, значение которой по величине является средним из трех возможных. То есть:
в ЭВМ-реализации можно принять условие: выбрать ту точку, значение которой по величине является средним из трех возможных. То есть:
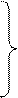
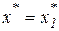 , если
, если 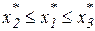 , или
, или 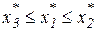 ;
;
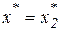 , если
, если 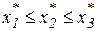 , или
, или 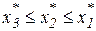 ; (17)
; (17)
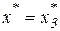 , если
, если 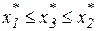 , или
, или 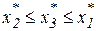 .
.
Кроме того, и это существенно, на выбор точки 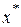 влияет также то, насколько близко точка
влияет также то, насколько близко точка 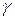 оказывается к точкам
оказывается к точкам 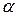 и
и 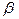 на числовой оси.
на числовой оси.
Если
а) 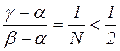 ,
,
или
б)  ,
,
то большое значение N в этих отношениях ( ) означает одностороннюю сходимость к стационарной точке, но не к точке локального минимума. Поэтому, при выполнении условия а) следует положить
) означает одностороннюю сходимость к стационарной точке, но не к точке локального минимума. Поэтому, при выполнении условия а) следует положить 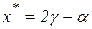 , а при выполнении условия б) принять точку
, а при выполнении условия б) принять точку 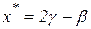 .
.
Начало
1
Ввод 
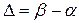

 Конец
Конец
проверка нет выбор
условий новой нет
критерия 2 тройки
да 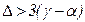
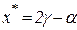
вычисление 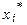
по (14)-(16) и
выбор по (17) 
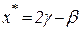
нет
14
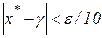
да
2 

да
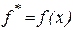
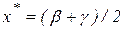
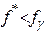
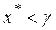
 2
2
да да
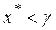
да
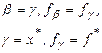

1
Схема 2.5. К методу парабол
* Леонардо Пизанский (1180-1240)–итальянский математик.
Метод пассивного поиска
Возьмем число h>0 (шаг поиска), такое, что  , где k > 1 - целое число. Будем вычислять значение функции
, где k > 1 - целое число. Будем вычислять значение функции 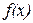 по формуле:
по формуле:
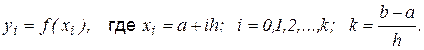 (2.2)
(2.2)
Из полученных значений выберем наименьшее:
 . (2.3)
. (2.3)
Тогда по критериям 1 и 2 можно утверждать, что точка  локального минимума находится на отрезке
локального минимума находится на отрезке  , где
, где
 . (2.4)
. (2.4)
Таким образом, минимум локализуется на промежутке длины не более 2 h и точка  – наилучшее приближение локального минимума среди всех
– наилучшее приближение локального минимума среди всех 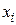 на
на  . (При необходимости можно продолжить локализацию функции
. (При необходимости можно продолжить локализацию функции 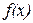 на отрезке
на отрезке  с шагом h 1 < h).
с шагом h 1 < h).
Пример поиска локального минимума функции методом пассивного поиска
Для функции  на отрезке
на отрезке  проведем пассивный поиск с шагом h = 1. Для этого по формуле (2.2) составим таблицу значений данной функции (табл. 2.1) с погрешностью 0.01 и построим ее график (рис.2.3).
проведем пассивный поиск с шагом h = 1. Для этого по формуле (2.2) составим таблицу значений данной функции (табл. 2.1) с погрешностью 0.01 и построим ее график (рис.2.3).
Таблица 2.1.

| - 5
| - 4
| - 3
| - 2
| - 1
| 0
| 1
| 2
| 3
| 4
| 5
|
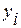
| 28.41
| -5.40
| -3.91
| 1.40
| 2.72
| 1.0
| 0.37
| 6.14
| 24.05
| 60.02
| 120.01
|
Из таблицы и графика (рис.2.3) видно, что на отрезке

, на интервалах (–
5. –3) и (
0. 2) имеются две точки локального минимума:

и
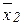
и соответствующие им локализующие тройки: {–
5, –4, –3 } и {
0, 1, 2 }, но абсолютный минимум достигается только в одной из них – при

= –
4.
В качестве подтверждения сказанному, проведем традиционный математический анализ данной функции по условиям (1.8), (1.9). Для этого вычислим первую и вторую производные функции 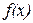 в окрестности точки
в окрестности точки 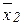 :
:  . Так как
. Так как  , а
, а  и
и  при всех x>0 (выполнено условие (1.9)), то на (0. 2) уравнение
при всех x>0 (выполнено условие (1.9)), то на (0. 2) уравнение 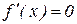 имеет единственное решение
имеет единственное решение 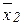 (стационарную точку функции по (1.8)), которая и является точкой минимума на
(стационарную точку функции по (1.8)), которая и является точкой минимума на 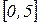 . Аналогичные вычисления в окрестности точки
. Аналогичные вычисления в окрестности точки  определят единственное решение на (– 5. –3). Поскольку на (– 3, 0) будет определена точка максимума
определят единственное решение на (– 5. –3). Поскольку на (– 3, 0) будет определена точка максимума  ,то точка
,то точка  является точкой минимума и на
является точкой минимума и на  . А так как других точек минимума на
. А так как других точек минимума на  нет, то, исходя из того, что
нет, то, исходя из того, что 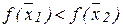 , можно сделать вывод - в точке
, можно сделать вывод - в точке  достигается глобальный минимум функции
достигается глобальный минимум функции  на отрезке
на отрезке 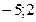 .
.
Оценка погрешности метода пассивного поиска
Оценим погрешность метода на отрезке  . Из условий (2.2)-(2.4) следует, что
. Из условий (2.2)-(2.4) следует, что 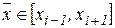 . Значит,
. Значит, 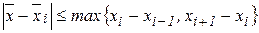 . Так как положение точки минимума
. Так как положение точки минимума 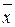 на отрезке
на отрезке  заранее неизвестно, то для
заранее неизвестно, то для  справедлива лишь следующая гарантированная оценка погрешности:
справедлива лишь следующая гарантированная оценка погрешности:
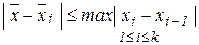 . (2.5)
. (2.5)
Величина, стоящая в правой части неравенства (2.5) станет минимальной, если точки  расположить на отрезке
расположить на отрезке  равномерно в соответствии с формулой (2.2). В случае такого выбора пробных точек метод пассивного поиска называется оптимальным и гарантированная оценка погрешности для него равна:
равномерно в соответствии с формулой (2.2). В случае такого выбора пробных точек метод пассивного поиска называется оптимальным и гарантированная оценка погрешности для него равна:
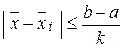 . (2.6)
. (2.6)
Поэтому вполне очевидно, что если бы для приведенного ранее примера потребовалось локализовать точку с погрешностью  на интервале, например,
на интервале, например,  , то для ее нахождения потребовалось бы провести вычисления в девяти пробных точках: -3.9, -3.8,...,-3.1. А для нахождения точки локального минимума на том же интервале, но с погрешностью
, то для ее нахождения потребовалось бы провести вычисления в девяти пробных точках: -3.9, -3.8,...,-3.1. А для нахождения точки локального минимума на том же интервале, но с погрешностью  , потребовало бы вычисления значений функции уже в 99 точках! Нетрудно заметить, что данный метод с уменьшением погрешности становится все менее и менее эффективным в смысле затрат машинного времени вычислений. Поэтому естественным становится вопрос о том, что если отрезок локализации уже найден, то как уменьшить эти затраты, не снижая при этом требований к точности вычислений минимума?
, потребовало бы вычисления значений функции уже в 99 точках! Нетрудно заметить, что данный метод с уменьшением погрешности становится все менее и менее эффективным в смысле затрат машинного времени вычислений. Поэтому естественным становится вопрос о том, что если отрезок локализации уже найден, то как уменьшить эти затраты, не снижая при этом требований к точности вычислений минимума?



 , где k > 1 - целое число. Будем вычислять значение функции
, где k > 1 - целое число. Будем вычислять значение функции 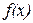 по формуле:
по формуле: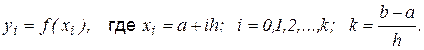 (2.2)
(2.2) . (2.3)
. (2.3) локального минимума находится на отрезке
локального минимума находится на отрезке  , где
, где . (2.4)
. (2.4) – наилучшее приближение локального минимума среди всех
– наилучшее приближение локального минимума среди всех 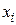 на
на  . (При необходимости можно продолжить локализацию функции
. (При необходимости можно продолжить локализацию функции  с шагом h 1 < h).
с шагом h 1 < h). на отрезке
на отрезке  проведем пассивный поиск с шагом h = 1. Для этого по формуле (2.2) составим таблицу значений данной функции (табл. 2.1) с погрешностью 0.01 и построим ее график (рис.2.3).
проведем пассивный поиск с шагом h = 1. Для этого по формуле (2.2) составим таблицу значений данной функции (табл. 2.1) с погрешностью 0.01 и построим ее график (рис.2.3).
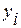
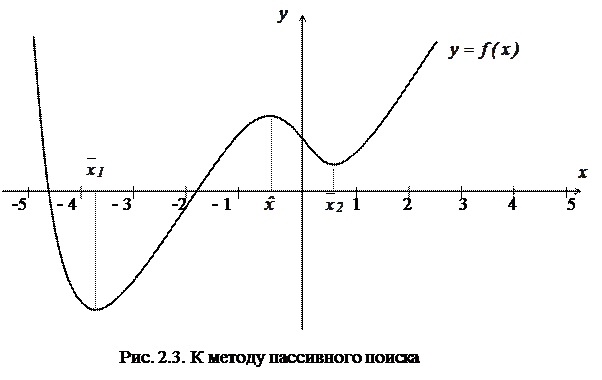
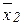 и соответствующие им локализующие тройки: {– 5, –4, –3 } и { 0, 1, 2 }, но абсолютный минимум достигается только в одной из них – при
и соответствующие им локализующие тройки: {– 5, –4, –3 } и { 0, 1, 2 }, но абсолютный минимум достигается только в одной из них – при  . Так как
. Так как  , а
, а  и
и  при всех x>0 (выполнено условие (1.9)), то на (0. 2) уравнение
при всех x>0 (выполнено условие (1.9)), то на (0. 2) уравнение 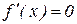 имеет единственное решение
имеет единственное решение 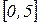 . Аналогичные вычисления в окрестности точки
. Аналогичные вычисления в окрестности точки  ,то точка
,то точка  . А так как других точек минимума на
. А так как других точек минимума на 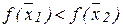 , можно сделать вывод - в точке
, можно сделать вывод - в точке 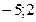 .
. точку
точку  локального минимума функции
локального минимума функции 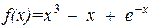 . Поиск будем производить на отрезке локализации
. Поиск будем производить на отрезке локализации  .
.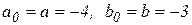 .
. ,
, 
 ,
, 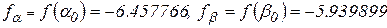 ;/
;/ и
и  . Так как
. Так как 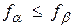 , то установим в качестве нового отрезка локализации отрезок
, то установим в качестве нового отрезка локализации отрезок  ;
;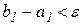 и
и  не выполняются, то произведем очередную итерацию.
не выполняются, то произведем очередную итерацию.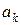
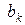
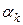


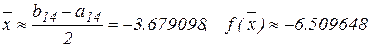 .
. называется такое разбиение отрезка на две неравные части точками
называется такое разбиение отрезка на две неравные части точками  и
и  , что отношение длины всего отрезка
, что отношение длины всего отрезка 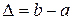 к длине его большей части
к длине его большей части  равно отношению длины большей части к длине
равно отношению длины большей части к длине  меньшей части:
меньшей части:  . При этом (рис.2.5) точки
. При этом (рис.2.5) точки 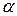 и
и  .
. и
и  .
.

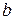
 и
и  на очередном шаге итерации находятся по формулам:
на очередном шаге итерации находятся по формулам: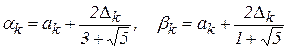 .
. на очередном шаге вычислений. Действительно, какой бы из отрезков
на очередном шаге вычислений. Действительно, какой бы из отрезков  или
или  не был бы выбран за очередной отрезок локализации, точка
не был бы выбран за очередной отрезок локализации, точка  , если
, если  и
и  , если
, если  ) совпадет с одной из точек
) совпадет с одной из точек 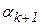 или
или  (рис 2.6). Поэтому на очередном шаге достаточно вычислить значение функции лишь в одной недостающей точке.
(рис 2.6). Поэтому на очередном шаге достаточно вычислить значение функции лишь в одной недостающей точке.


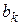


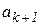
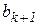
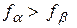
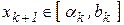
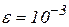 точку
точку 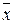 локального минимума функции
локального минимума функции  на отрезке локализации
на отрезке локализации  .
.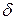 ; вместо вычислений
; вместо вычислений  и
и 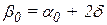 установить соответственно
установить соответственно 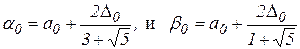 ; добавить вычисление величины
; добавить вычисление величины  .
.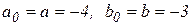 имеем:
имеем: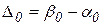 ,
, 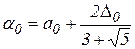 ,
,  и определим значения
и определим значения 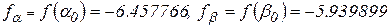 ;
;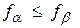 , то установим в качестве нового отрезка локализации отрезок
, то установим в качестве нового отрезка локализации отрезок 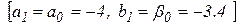 ;
; не выполняются, то произведем очередную итерацию.
не выполняются, то произведем очередную итерацию.
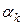


 .
. – локального минимума функции
– локального минимума функции 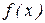 , т.е. получена локализующая тройка
, т.е. получена локализующая тройка  В качестве такой тройки можно воспользоваться, например, вычислениями, полученными на трех последних шагах (
В качестве такой тройки можно воспользоваться, например, вычислениями, полученными на трех последних шагах (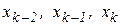 ) методом пассивного поиска. При этом соответствие между
) методом пассивного поиска. При этом соответствие между 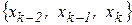 нужно установить так, чтобы выполнялось условие критерия 2:
нужно установить так, чтобы выполнялось условие критерия 2: 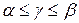 . Вложенная в
. Вложенная в 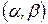 новая локализующая тройка строится при помощи интерполяционного полинома Ньютона
новая локализующая тройка строится при помощи интерполяционного полинома Ньютона 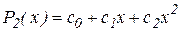 . График полинома
. График полинома 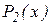 является параболой (рис.2.5.1), проходящей через три точки плоскости с координатами
является параболой (рис.2.5.1), проходящей через три точки плоскости с координатами  . Точка минимума
. Точка минимума  полинома
полинома  . Вычислив
. Вычислив 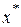 и
и 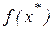 , сравним значение
, сравним значение 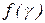 и по критерию 2 найдем новую локализирующую тройку.
и по критерию 2 найдем новую локализирующую тройку.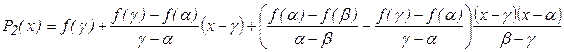 (13)
(13) y
y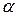
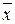
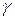
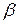 x
x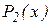 представлены формулами:
представлены формулами: ;
;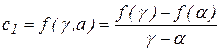 ;
; .
.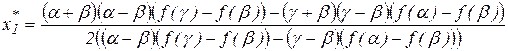 , (14)
, (14) , (15)
, (15)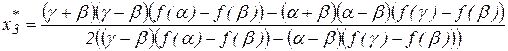 . (16)
. (16) следует сделать по тому представлению, которое будет вычисляться с меньшей потерей точности (значащих цифр в разностях). Однако, такой выбор на ЭВМ осуществить достаточно трудоемко. Поэтому, для определения конкретной точки
следует сделать по тому представлению, которое будет вычисляться с меньшей потерей точности (значащих цифр в разностях). Однако, такой выбор на ЭВМ осуществить достаточно трудоемко. Поэтому, для определения конкретной точки 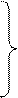
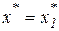 , если
, если 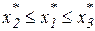 , или
, или 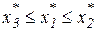 ;
;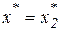 , если
, если 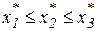 , или
, или 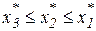 ; (17)
; (17)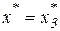 , если
, если 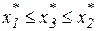 , или
, или 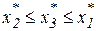 .
.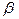 на числовой оси.
на числовой оси.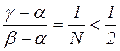 ,
, ,
, ) означает одностороннюю сходимость к стационарной точке, но не к точке локального минимума. Поэтому, при выполнении условия а) следует положить
) означает одностороннюю сходимость к стационарной точке, но не к точке локального минимума. Поэтому, при выполнении условия а) следует положить 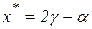 , а при выполнении условия б) принять точку
, а при выполнении условия б) принять точку 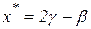 .
.

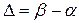

 Конец
Конец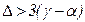
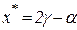
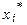

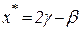
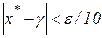


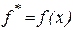
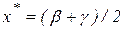
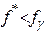
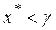
 2
2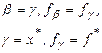

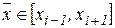 . Значит,
. Значит, 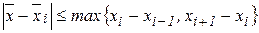 . Так как положение точки минимума
. Так как положение точки минимума 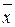 на отрезке
на отрезке 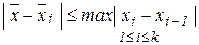 . (2.5)
. (2.5) расположить на отрезке
расположить на отрезке 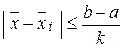 . (2.6)
. (2.6) на интервале, например,
на интервале, например,  , то для ее нахождения потребовалось бы провести вычисления в девяти пробных точках: -3.9, -3.8,...,-3.1. А для нахождения точки локального минимума на том же интервале, но с погрешностью
, то для ее нахождения потребовалось бы провести вычисления в девяти пробных точках: -3.9, -3.8,...,-3.1. А для нахождения точки локального минимума на том же интервале, но с погрешностью  , потребовало бы вычисления значений функции уже в 99 точках! Нетрудно заметить, что данный метод с уменьшением погрешности становится все менее и менее эффективным в смысле затрат машинного времени вычислений. Поэтому естественным становится вопрос о том, что если отрезок локализации уже найден, то как уменьшить эти затраты, не снижая при этом требований к точности вычислений минимума?
, потребовало бы вычисления значений функции уже в 99 точках! Нетрудно заметить, что данный метод с уменьшением погрешности становится все менее и менее эффективным в смысле затрат машинного времени вычислений. Поэтому естественным становится вопрос о том, что если отрезок локализации уже найден, то как уменьшить эти затраты, не снижая при этом требований к точности вычислений минимума?

