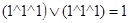Предположим, что произвольная логическая функция n аргументов задана единственным набором аргументов, при котором эта функция принимает значение 1.
Составим конъюнкцию (логическую функцию «И») от всех n аргументов: аргументы, которые в указанном наборе равны 0, возьмем со знаком инверсии, а аргументы, равные 1 в указанном наборе – без знака инверсии, так как согласно определению конъюнкции, чтобы логическая функция «И» принимала значение 1, необходимо, чтобы все аргументы были равны 1.
Пример 1.1. Задана логическая функция F от четырех аргументов X1, X2, X3, X4, которая принимает значение 1 при наборе X1=0, X2=1, X3=1, X4=0 и 0 при всех остальных наборах. Составить выражение для F.
Составим выражение для этой функции:
F(X1, X2, X3, X4) =  или F(X1, X2, X3, X4) =
или F(X1, X2, X3, X4) = 
Предположим, что произвольная логическая функция n аргументов, задана единственным набором аргументов, при котором эта функция принимает значение 0.
Составим дизъюнкцию (логическую функцию «ИЛИ») от всех n аргументов следующим образом: аргументы, равные 0 в заданном наборе, возьмем без знака инверсии, а аргументы, равные в заданном наборе 1, - со знаком инверсии, так как согласно определению дизъюнкции, чтобы логическая функция «ИЛИ» принимала значение 0, необходимо, чтобы все аргументы были равны 0.
Пример 1.2. Задана логическая функция F от четырех аргументов X1, X2, X3, X4, которая принимает значение 1 при наборе X1=0, X2=1, X3=1,X4=1 и 1 при всех остальных наборах. Составить выражение для F.
Составим выражение для этой функции:
F(X1, X2, X3, X4) = 

Логическая функция n аргументов может быть выражена через логические функции «И», «ИЛИ» и «НЕ» (конъюнкцию, дизъюнкцию, отрицание) по следующему правилу:
- сначала составляется конъюнкция всех значений переменных по описанному выше правилу, при которых функция равна 1;
- затем образуется дизъюнкция всех этих конъюнкций.
Пример 1.3. Задана логическая функция F от четырех аргументов X1, X2, X3, X4, которая принимает значение 1 при наборах
X1=1, X2=0, X3=1, X4=0
X1=0, X2=0, X3=1, X4=1
X1=1, X2=1, X3=0, X4=1
и 0 при всех остальных наборах. Составить выражение для F.
Функция, сформированная таким образом, будет иметь вид:
F(X1, X2, X3, X4) = 
Для более полного восприятия символ конъюнкции обычно опускают, тогда
F(X1, X2, X3, X4) = 
Для любого из перечисленных наборов функция F(X1, X2, X3, X4), будет представлять собой дизъюнкцию одной 1 и остальных 0, т.е. будет равна 1. На остальных наборах будет представлять собой дизъюнкцию одних нулей, т.е. будет равна 0.
Произвольная логическая функция, заданная перечислением всех наборов аргументов, при которых она принимает значение 0, определяется следующим образом: для каждого из этих наборов составляется дизъюнкция, а затем образуется конъюнкция всех этих дизъюнкций.
Пример 1.4. Задана логическая функция F от трех аргументов X1, X2, X3, которая принимает значение 0 при наборах
X1=0, X2=1, X3=1
X1=1, X2=0, X3=0
X1=0, X2=0, X3=0
и 1 при всех остальных наборах. Составить выражение для F.
Функция, сформированная таким образом, будет иметь вид:
F(X1, X2, X3) = (

Для любого из перечисленных наборов функция F(X1, X2, X3, X4), будет представлять собой конъюнкцию одного 0 и остальных 1, т.е. будет равна 0. На остальных наборах будет представлять собой дизъюнкцию одних единиц, т.е. будет равна 1.
Логические функции, представляющие собой дизъюнкции отдельных членов, каждый из которых есть в свою очередь некоторая функция, содержащая только конъюнкции и инверсии, называются логическими функциями дизъюнктивной формы.
Логические функции дизъюнктивной формы, в которых инверсия применяется лишь непосредственно к аргументам, например, (X 
 Z), но не к более сложным функциям, как, например,
Z), но не к более сложным функциям, как, например, 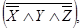 называются дизъюнктивными нормальными функциями (ДНФ).
называются дизъюнктивными нормальными функциями (ДНФ).
Если каждый член дизъюнктивной нормальной функции от n аргументов содержит все n аргументов, часть из которых со знаком инверсии, а часть без него, то функция называется совершенной (СДНФ). Например, функция
F(X1, X2, X3, X4) = 
представляет собой – СДНФ.
Каждый член такой формы обращается в 1 лишь при некотором единственном наборе аргументов, а число членов равно числу разных наборов, обращающих функцию в единицу.
В несовершенных дизъюнктивных нормальных функциях от n аргументов некоторые члены содержат количество аргументов, меньшее, чем n. Такие члены принимают значение 1 при нескольких наборах аргументов. Потому и число членов в несовершенных формах меньше, чем число членов в совершенных формах этих же функций.
Аналогично функция,
F(X1, X2, X3) = (
Представляет собой совершенную конъюнктивную нормальную форму логических функций – СКНФ.
Пример 1.5. Составить выражение для функции, принимающей значение 1 на наборах 2 и 6.
Запишем числа 2 и 6 в двоичной системе: 2 в двоичной системе 10, 6 в двоичной системе -110.
После перевода в двоичную систему числа 2 и 6 занимают неодинаковое количество позиций, поэтому количество переменных, от которых зависит функция, берем равным максимальному количеству позиций, занимаемых при записи каждого из чисел: 2 в двоичной системе 010, 6 в двоичной системе -110.
Это значит, что искомая функция будет функцией от 3 переменных: X1, X2, X3.
Наборы, на которых функция обращается в 1:
(210=0102) X1=0, X2=1, X3=0
(610=1102) X1=1, X2=1, X3=0.
Составим выражение для функции
F(X1, X2, X3) = ( , т.е. значение переменной – значение соответствующей позиции на наборе:
, т.е. значение переменной – значение соответствующей позиции на наборе:
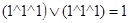
Функция F(X1, X2, X3) – СДНФ.
Пример 2.6. F=0 на наборах 2, 4. Составить выражение для этой функции:
2 в двоичной системе 10(или 010),
4 в двоичной системе -100.
Наборы, на которых функция обращается в 0:
X1=0, X2=1, X3=0
X1=1, X2=0, X3=0
Логическая функция принимает вид:
F(X1, X2, X3) = (
Функция F(X1, X2, X3) – СКНФ.



 или F(X1, X2, X3, X4) =
или F(X1, X2, X3, X4) = 






 Z), но не к более сложным функциям, как, например,
Z), но не к более сложным функциям, как, например, 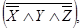 называются дизъюнктивными нормальными функциями (ДНФ).
называются дизъюнктивными нормальными функциями (ДНФ).

 , т.е. значение переменной – значение соответствующей позиции на наборе:
, т.е. значение переменной – значение соответствующей позиции на наборе: