Геометрическое доказательство теоремы Пифагора

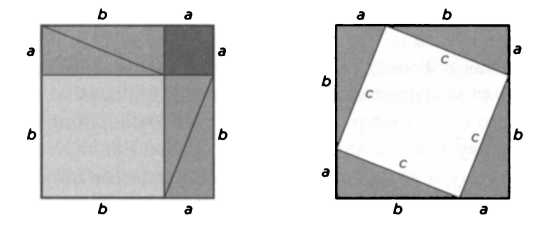
Возьмем два квадрата одинаковой площади со стороной а + b и разделим их, как показано на рисунке. Очевидно, что площадь каждого из квадратов равна (а + b)², но ее можно выразить и другим способом. В квадрате слева общая площадь равна сумме площадей двух квадратов со сторонами b и а и площадей четырех треугольников со сторонами а и b, то есть  

1/2 · ab  

для каждого из них. Следовательно, общая площадь первого квадрата равна  

A₁ = a² + b² + 4(1/2 · ab)  

Площадь второго квадрата равна сумме площади вписанного квадрата со стороной с и площадей четырех треугольников со сторонами а и b:  

A₂ = c² + 4(1/2 · ab).  

Так как А₁ и А₂ равны, то  

a² + b² + 4(1/2 · ab) = c² + 4(1/2 · ab).  

И, после сокращения уравнения:  

а²+b²=с².  

Это типичный пример геометрического доказательства, поскольку для него необходимо построить различные геометрические фигуры внутри квадратов.  

Поэтому он заслуживает титула отца математики. Все амбиции математической науки, одной из самых плодотворных в интеллектуальной истории человечества, выразил немецкий математик Давид Гильберт (1862‑1943) в своем "Wir mussen wissen. Wir werden wissen" ("Мы должны знать. Мы будем знать!") во втором десятилетии XX века.

Пифагор или кто‑то из его школы доказал теорему, носящую его имя, так что уже невозможно сомневаться в ее истинности. Данная теорема дает нам неизменное правило. В случае с прямоугольным треугольником это отношение всегда будет выполняться. Пифагор очень высоко поднял планку для последующих поколений: уже недостаточно было найти правило, проверить его на практике много раз и признать его истинным. Теперь в математике требовалось его доказывать. И хотя в некоторых случаях это чрезвычайно сложно, подход Пифагора оказался таким плодотворным, что математики, несмотря на все трудности, не готовы отказываться от него.

В течение нескольких веков греки следовали принципам Пифагора и стремились к строгому доказательству своих результатов. Но геометр, который жил при Птолемее I (367‑283 до н. э.), военачальнике Александра Великого и царе Египта, пошел еще дальше. Речь идет о Евклиде (ок. 325‑265 до н. э.), который не довольствовался тем, чтобы доказывать отдельные результаты, а амбициозно захотел собрать все математическое знание своего времени в одну систему.

Евклид понял, что любое доказательство основывается на предыдущих результатах, которые, в свою очередь, были доказаны ранее. Но данный процесс не может длиться до бесконечности – нужно исходить из некоторых истин, которые считаются очевидными. Их Евклид называл аксиомами. Также должны существовать четкие определения используемых элементов; в геометрии, например, это точки, линии, треугольники, круги и так далее. На этой основе Евклид создал единую систему, в которой доказанные и предполагаемые результаты (в последнем случае – аксиомы) служат основой для доказательства других результатов. В отличие от аксиом, эти новые результаты, требующие доказательства, получили название теорем.

Повторяя эту операцию снова и снова, мы можем построить математическую теорию, похожую на дерево, на котором с помощью небольшого количества корней можно породить потенциально бесконечное количество веток и листьев. Какие‑ то из них более важны (более крепкие и плодородные в своем потенциале создания новых ветвей), чем другие, но все они одинаково истинные.

Рассказывают, что Птолемей I потребовал у Евклида обучить его математике, при этом не желая тратить много сил и времени. Он хотел, чтобы ученый упростил свои объяснения, на что тот ответил:

"Ваше Величество, то, о чем Вы меня просите, невозможно; необходимо пережить и пройти через все необходимые шаги, чтобы понять науку. Не существует царской дороги в математику".

Невозможно преувеличить важность евклидовой геометрии. Практически все последующие поколения математиков использовали ее в качестве отправной точки. Сегодня любой математик, предлагающий новую теорию (или пытающийся переформулировать существующую), пользуется системой Евклида. До самого XX века его книга – знаменитые "Начала" – была самой популярной после Библии и считалась отправной точкой и необходимым объектом изучения в университетах.

Но несмотря на невероятные результаты, некоторые нюансы деятельности Пифагора и школы, которую он основал, сегодня могут показаться неприемлемыми. Пифагорейцы представляли собой что‑то вроде тайной религии или секты и, возможно, не сильно отличались от других секретных древнегреческих обществ, например элевсинских или орфических мистерий. Так же как и посвященные элевсинцы, пифагорейцы не могли открывать природу своей деятельности.

Пифагорейский мистицизм был тесно связан с идеей того, что число – это сущность природы. Но под числом пифагорейцы понимали не совсем то же, что и мы. Для них числа были только натуральными и теми, что могут быть выражены в виде частного натуральных (3/4,5/8 и так далее): множество рациональных положительных чисел.

Конечно, пифагорейцы умели измерять геометрические длины. Верные своей мистической вере в числовую сущность природы, они были уверены, что любую длину можно выразить рациональным положительным числом. Они ожидали, что геометрия будет открывать природу, подобно любой естественной науке или музыкальной гармонии, также открытой ими.

И тут произошла катастрофа. Согласно легенде, один из учеников Пифагора доказал, что гипотенуза прямоугольного треугольника не является числом в том смысле, который назначали этому понятию пифагорейцы. Как ни удивительно, речь шла о самым простом прямоугольном треугольнике, у которого два катета имеют длину, равную единице, – о треугольнике не только прямоугольном, но и равнобедренном. Действительно, в данном случае гипотенуза, согласно собственно теореме Пифагора, равна √2.

Но √2 нельзя выразить в виде рационального положительного числа! Это то, что мы сегодня называем иррациональным числом, так как его нельзя выразить в виде отношения между двумя натуральными числами. Именно это, как говорит легенда, доказал Гиппас из Метапонта (ок. 500 до н. э.), строптивый ученик, за что его (или за то, что он открыл миру свое доказательство), как говорят, утопили в море рядом с Кротоной. Здесь мы видим типичный случай доказательства от противного, в котором предполагается противоположное тому, что нужно доказать, и, в свою очередь, доказывается, что это предположение приводит к неразрешимому противоречию с уже доказанной истиной. Это один из самых мощных способов доказательства в математике, при котором, как говорил британский ученый Годфри Харди (1877‑1947), математик рискует сильнее, чем любой шахматист с его гамбитом: он рискует всей игрой.

Интеллектуальная гордость пифагорейцев перенесла тяжелейший удар: мир, по‑видимому, не был основан на числе как основной сущности. Пифагорейцам не пришло в голову, что достаточно пересмотреть их ограниченное понятие числа, чтобы решить дилемму. Но это объяснимо; на заре математики для пифагорейцев было невозможно принять то, что им казалось невыразимым. В конце концов, они были вынуждены провести различие между величиной и числом, между длинами, измеряемыми в геометрии, и числами, выражаемыми арифметически. Так, обе дисциплины начали отдаляться друг от друга, и только работы ученых XVI и XVII веков Франсуа Виета, Ферма и Рене Декарта смогли воссоединить их.

ДОКАЗАТЕЛЬСТВО ИРРАЦИОНАЛЬНОСТИ √2

Представим, что число √2 рационально. Тогда его можно выразить в виде отношения двух целых чисел: √2 =p/q. Мы можем предположить, что предыдущее отношение несократимо, то есть его нельзя упростить еще больше, или, что то же самое, р и q не имеют общих делителей. Итак, из предыдущего выражения следует, что 2 = p²/q². Следовательно, p² – четное. Но если целое число в квадрате четное, то и само число, p, тоже четное (поскольку квадрат нечетного числа всегда нечетный). Следовательно, мы можем записать p = 2k и 4k² = 2q², или 2k² = q². То есть q² также четное, и q тоже. Но это противоречит гипотезе о том, что у p и q нет общих делителей! Следовательно, одна из наших гипотез ложная. Это не может быть гипотеза о том, что отношение несократимо; то есть ложно предположение о том, что √2 – рациональное число.