Полугруппа В называется циклической (моногенной), если в ней содержится такой элемент а, что всякий элемент х из В может быть записан в форме  для некоторого n >0. Элемент а называется образующим (порождающим) циклической полугруппы. Важнейшим примером циклической полугруппы является полугруппа Р положительных целых чисел относительно сложения. Её образующим служит 1. Зафиксируем положительные числа n и d и рассмотрим разбиение
для некоторого n >0. Элемент а называется образующим (порождающим) циклической полугруппы. Важнейшим примером циклической полугруппы является полугруппа Р положительных целых чисел относительно сложения. Её образующим служит 1. Зафиксируем положительные числа n и d и рассмотрим разбиение  множества Р, состоящее из одноэлементных классов [1]={1}, [2]={2},…,[d-1]={d-1} и бесконечных классов
множества Р, состоящее из одноэлементных классов [1]={1}, [2]={2},…,[d-1]={d-1} и бесконечных классов
[d]={d, d+n, d+2n, …, d+kn,…},
[d+1]={d+1, d+1+n, d+1+2n,…, d+1+kn,…},
[d+(n-1)]={d+(n-1), d+(n-1)+n, d+(n-1)+2n,…,d+(n-1)+kn,…}.
Убедимся, что это разбиение допустимо. В самом деле, пусть х, u 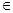 [ I ], y,v
[ I ], y,v 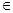 [ j ], где 1
[ j ], где 1 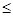 I, j< d+n. Возможны следующие четыре случая: 1) I, j <d; 2) I< d, j
I, j< d+n. Возможны следующие четыре случая: 1) I, j <d; 2) I< d, j 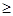 d; 3) I
d; 3) I 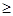 d, j< d; 4) I, j
d, j< d; 4) I, j 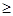 d. В первом случае имеем: x=u=I и y=v=j, откуда [x+y]=[u+v], поскольку x+y=u+v. Во втором случае x=u=I, y=j+kn и v=j+Ln для подходящих k,L. Используя деление с остатком запишем
d. В первом случае имеем: x=u=I и y=v=j, откуда [x+y]=[u+v], поскольку x+y=u+v. Во втором случае x=u=I, y=j+kn и v=j+Ln для подходящих k,L. Используя деление с остатком запишем
I + j - d=sn + r,
где 0 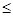 r< n. Тогда
r< n. Тогда
x + y = I + j + kn = d + (I + j – d) + kn = d + r + (s + k) n
и u + v = I + j + Ln = d + (I + j – d) + Ln = d + r + (s + L) n,
откуда [x + y] = [d + r] = [u + v]. Третий случай рассматривается аналогично. В четвертом случае, используя определение смежных классов, можно записать
x =I + kn = d + (I – d) + kn,
u = I + Ln = d + (I – d) + Ln,
y = j + pn = d + (j – d) + pn,
v = j + qn = d + (j – d) + qn.
Тогда
x + y = d + (d + (I – d) + (j – d)) + (k + p) n
и
u + v = d + (d +(I – d) + (j – d)) + (L + q) n.
Разделив с остатком, получим
d + (I – d) + (j – d) = sn + r,
где 0 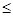 r< n. Отсюда
r< n. Отсюда
x + y = d + r + (k + p + s) n
и
u + v = d + r + (L + q + s) n,
т.е. [x + y] = [d + r] = [u + v].
Факторполугруппу полугруппы Р по рассмотренному разбиению называют циклом с хвостом.

При d = 1 хвост оказывается пустым. Такую полугруппу называют циклом.
Теорема.
Всякая циклическая полугруппа изоморфна или аддитивной полугруппе Р положительных чисел, или некоторому циклу с хвостом (возможно пустым).
Доказательство. Пусть В – циклическая полугруппа с образующим а. Рассмотрим отображение полугруппы Р в полугруппу В, определяемое условием  .
.
Ввиду циклической полугруппы В, 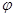 оказывается наложением. В силу теоремы: “
оказывается наложением. В силу теоремы: “ 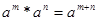 для всех m, n > 0.”
для всех m, n > 0.” 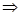
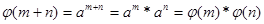 ,
,
т.е. 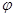 является гомоморфизмом. Из следующей теоремы:
является гомоморфизмом. Из следующей теоремы:
Если  - гомоморфное наложение полугрупп и
- гомоморфное наложение полугрупп и 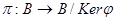 - естественный гомоморфизм, то существует изоморфизм
- естественный гомоморфизм, то существует изоморфизм  такой, что
такой, что  , вытекает, что В изоморфна факторполугруппе Р/
, вытекает, что В изоморфна факторполугруппе Р/  , где
, где  =
= 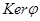 . Если все классы разбиения
. Если все классы разбиения  одноэлементны, то В изоморфна Р. В противном случае обозначим через d наименьшее целое число, входящее в неодноэлементный класс, а число n выберем так, чтобы d + n было наименьшим числом, отличным от d, но входящим в один класс с d. Тогда имеем классы [1], [2],…, [d – 1], [d], [d + 1],…, [d + n – 1], среди которых первые d – 1 одноэлементные и [d]
одноэлементны, то В изоморфна Р. В противном случае обозначим через d наименьшее целое число, входящее в неодноэлементный класс, а число n выберем так, чтобы d + n было наименьшим числом, отличным от d, но входящим в один класс с d. Тогда имеем классы [1], [2],…, [d – 1], [d], [d + 1],…, [d + n – 1], среди которых первые d – 1 одноэлементные и [d]  [d + I] при I= 1,2,…, n – 1. Докажем, что
[d + I] при I= 1,2,…, n – 1. Докажем, что
[d + I] = [d + I + kn] (*)
при любых I и k. В силу определения разбиения  , для этого достаточно установить, что
, для этого достаточно установить, что
 . (**)
. (**)
При k = 0 это очевидно. Допустим, что (**) доказано при всех I и
k = 0,1,…, t – 1. Тогда, вспоминая, что  , получаем
, получаем
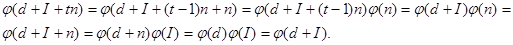
Тем самым равенство (**), а значит (*), доказано. Остаётся убедится, что разбиение 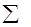 совпадает с разбиением
совпадает с разбиением 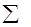 (d +n). С этой целью заметим, что одноэлементные классы этих разбиений совпадают. Ввиду равенства (*), для доказательства совпадения бесконечных классов достаточно установить, что смежные классы [d + I] и [d + j] разбиения
(d +n). С этой целью заметим, что одноэлементные классы этих разбиений совпадают. Ввиду равенства (*), для доказательства совпадения бесконечных классов достаточно установить, что смежные классы [d + I] и [d + j] разбиения 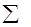 , где
, где  , различны. Но если [d + I] = = [d + j], то
, различны. Но если [d + I] = = [d + j], то
[d] = [d + n] = [d + j] + [n – j] = [d + I] + [n – j] = [d + (n – (j – I))]
и, поскольку 0< n – (j – I)<n, мы вступаем в противоречие с выбором числа n. Ч.т.д.



 для некоторого n >0. Элемент а называется образующим (порождающим) циклической полугруппы. Важнейшим примером циклической полугруппы является полугруппа Р положительных целых чисел относительно сложения. Её образующим служит 1. Зафиксируем положительные числа n и d и рассмотрим разбиение
для некоторого n >0. Элемент а называется образующим (порождающим) циклической полугруппы. Важнейшим примером циклической полугруппы является полугруппа Р положительных целых чисел относительно сложения. Её образующим служит 1. Зафиксируем положительные числа n и d и рассмотрим разбиение  множества Р, состоящее из одноэлементных классов [1]={1}, [2]={2},…,[d-1]={d-1} и бесконечных классов
множества Р, состоящее из одноэлементных классов [1]={1}, [2]={2},…,[d-1]={d-1} и бесконечных классов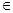 [ I ], y,v
[ I ], y,v 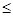 I, j< d+n. Возможны следующие четыре случая: 1) I, j <d; 2) I< d, j
I, j< d+n. Возможны следующие четыре случая: 1) I, j <d; 2) I< d, j 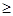 d; 3) I
d; 3) I 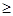 d. В первом случае имеем: x=u=I и y=v=j, откуда [x+y]=[u+v], поскольку x+y=u+v. Во втором случае x=u=I, y=j+kn и v=j+Ln для подходящих k,L. Используя деление с остатком запишем
d. В первом случае имеем: x=u=I и y=v=j, откуда [x+y]=[u+v], поскольку x+y=u+v. Во втором случае x=u=I, y=j+kn и v=j+Ln для подходящих k,L. Используя деление с остатком запишем 
 .
.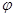 оказывается наложением. В силу теоремы: “
оказывается наложением. В силу теоремы: “ 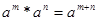 для всех m, n > 0.”
для всех m, n > 0.” 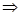
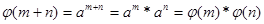 ,
, - гомоморфное наложение полугрупп и
- гомоморфное наложение полугрупп и 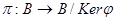 - естественный гомоморфизм, то существует изоморфизм
- естественный гомоморфизм, то существует изоморфизм  такой, что
такой, что  , вытекает, что В изоморфна факторполугруппе Р/
, вытекает, что В изоморфна факторполугруппе Р/  , где
, где 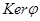 . Если все классы разбиения
. Если все классы разбиения  [d + I] при I= 1,2,…, n – 1. Докажем, что
[d + I] при I= 1,2,…, n – 1. Докажем, что . (**)
. (**) , получаем
, получаем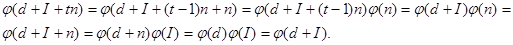
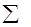 совпадает с разбиением
совпадает с разбиением  , различны. Но если [d + I] = = [d + j], то
, различны. Но если [d + I] = = [d + j], то

