Содержание
Введение------------------------------------------------------------------- 3
1. Понятие свободной полугруппы------------------------- 4
1.1. Слова------------------------------------------------------------ 4
1.2. Понятие свободной полугруппы-------------------------- 5
2. Применение--------------------------------------------------- 9
2.1. Циклические (моногенные) полугруппы--------------- 9
2.2. Сводные коммутативные полугруппы------------------ 12
2.3. Упражнения-------------------------------------------------- 13
3. Обзор результатов по проблеме Туэ-------------------- 15
Литература-----------------------------------------------------------
Введение
Дипломная работа посвящена теории свободных полугрупп. Свободные алгебраические объекты играют важную роль в общей алгебре, поскольку любая алгебраическая структура является гомоморфным образом свободной алгебраической структуры того же типа.
В теории полугрупп свободные объекты описываются конструктивно, именно как полугруппы слов над некоторым алфавитом. Поэтому большое место в работе уделено рассмотрению свойств полугрупп слов. Эти свойства носят, как правило, комбинаторный характер.
Кроме того, в работе изучаются и абстрактные свойства свободных полугрупп и некоторых связанных с ним полугрупп.
В первом параграфе вводятся основные понятия и доказательства теорем о существовании и единственности свободных полугрупп с множеством образующих данной мощности.
Второй параграф посвящён двум применениям свободных полугрупп:
1) описание циклических полугрупп;
2) свободной коммутативной полугруппе.
Там же доказываются некоторые комбинаторные свойства слов над произвольным алфавитом.
В третьем параграфе даётся обзор проблематики Туэ о существовании бесквадратных и бескубных слов произвольной длины над различными алфавитами.
В дипломной работе используются книги [1 - 4] из приведённого списка библиографии.
Понятие свободной подгруппы
Слова
Алфавит А – это непустое конечное множество. Буквы (символы)- элементы алфавита А. Слово над алфавитом А – это конечная цепочка, состоящая из нуля или более букв из А, причем одна и та же буква может входить несколько раз. Цепочка, состоящая из нулевого количества букв, называется пустым словом и обозначается 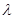 . Таким образом
. Таким образом 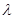 , 0, 1, 010, 1111 суть слова над алфавитом А ={0, 1}. Множество всех слов над алфавитом А обозначается W(A), а множество всех непустых слов обозначается Z(A).
, 0, 1, 010, 1111 суть слова над алфавитом А ={0, 1}. Множество всех слов над алфавитом А обозначается W(A), а множество всех непустых слов обозначается Z(A).
Если u и v – слова над алфавитом А, то их катенация xy (результат приписывания) – тоже слово над А:  и
и 

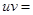
 . Катенация является ассоциативной операцией, и пустое множество служит единицей по отношению к ней: x
. Катенация является ассоциативной операцией, и пустое множество служит единицей по отношению к ней: x 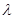 =
= 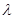 x=
x= 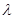 для всех x. Если х – слово, а i – натуральное число, то
для всех x. Если х – слово, а i – натуральное число, то 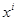 обозначает слово, полученное катенацией i слов, каждое из которых есть х.
обозначает слово, полученное катенацией i слов, каждое из которых есть х.
 Длина слова х, обозначается
Длина слова х, обозначается  , есть число букв в х, причем каждая буква считается столько раз, сколько раз она входит в х. Опять по определению
, есть число букв в х, причем каждая буква считается столько раз, сколько раз она входит в х. Опять по определению 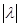 =0. Функция длины обладает некоторыми свойствами логарифма: для всех слов х, у и неотрицательных некоторых i
=0. Функция длины обладает некоторыми свойствами логарифма: для всех слов х, у и неотрицательных некоторых i
 ,
, 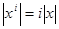 .
.
В теории языков важнейшей операцией является операция морфизма. Морфизмом называется отображение h: W(A) 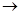 M(A), где W(A) и M(A) –множества всех слов удовлетворяющие условию h(xy)=h(x)h(y) для всех слов х,у.
M(A), где W(A) и M(A) –множества всех слов удовлетворяющие условию h(xy)=h(x)h(y) для всех слов х,у.
Теорема.
Всякая циклическая полугруппа изоморфна или аддитивной полугруппе Р положительных чисел, или некоторому циклу с хвостом (возможно пустым).
Доказательство. Пусть В – циклическая полугруппа с образующим а. Рассмотрим отображение полугруппы Р в полугруппу В, определяемое условием  .
.
Ввиду циклической полугруппы В, 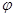 оказывается наложением. В силу теоремы: “
оказывается наложением. В силу теоремы: “ 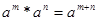 для всех m, n > 0.”
для всех m, n > 0.” 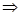
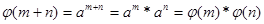 ,
,
т.е. 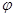 является гомоморфизмом. Из следующей теоремы:
является гомоморфизмом. Из следующей теоремы:
Если  - гомоморфное наложение полугрупп и
- гомоморфное наложение полугрупп и 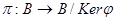 - естественный гомоморфизм, то существует изоморфизм
- естественный гомоморфизм, то существует изоморфизм  такой, что
такой, что  , вытекает, что В изоморфна факторполугруппе Р/
, вытекает, что В изоморфна факторполугруппе Р/  , где
, где  =
= 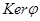 . Если все классы разбиения
. Если все классы разбиения  одноэлементны, то В изоморфна Р. В противном случае обозначим через d наименьшее целое число, входящее в неодноэлементный класс, а число n выберем так, чтобы d + n было наименьшим числом, отличным от d, но входящим в один класс с d. Тогда имеем классы [1], [2],…, [d – 1], [d], [d + 1],…, [d + n – 1], среди которых первые d – 1 одноэлементные и [d]
одноэлементны, то В изоморфна Р. В противном случае обозначим через d наименьшее целое число, входящее в неодноэлементный класс, а число n выберем так, чтобы d + n было наименьшим числом, отличным от d, но входящим в один класс с d. Тогда имеем классы [1], [2],…, [d – 1], [d], [d + 1],…, [d + n – 1], среди которых первые d – 1 одноэлементные и [d]  [d + I] при I= 1,2,…, n – 1. Докажем, что
[d + I] при I= 1,2,…, n – 1. Докажем, что
[d + I] = [d + I + kn] (*)
при любых I и k. В силу определения разбиения  , для этого достаточно установить, что
, для этого достаточно установить, что
 . (**)
. (**)
При k = 0 это очевидно. Допустим, что (**) доказано при всех I и
k = 0,1,…, t – 1. Тогда, вспоминая, что  , получаем
, получаем
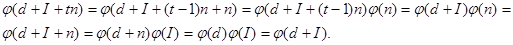
Тем самым равенство (**), а значит (*), доказано. Остаётся убедится, что разбиение 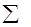 совпадает с разбиением
совпадает с разбиением 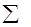 (d +n). С этой целью заметим, что одноэлементные классы этих разбиений совпадают. Ввиду равенства (*), для доказательства совпадения бесконечных классов достаточно установить, что смежные классы [d + I] и [d + j] разбиения
(d +n). С этой целью заметим, что одноэлементные классы этих разбиений совпадают. Ввиду равенства (*), для доказательства совпадения бесконечных классов достаточно установить, что смежные классы [d + I] и [d + j] разбиения 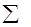 , где
, где  , различны. Но если [d + I] = = [d + j], то
, различны. Но если [d + I] = = [d + j], то
[d] = [d + n] = [d + j] + [n – j] = [d + I] + [n – j] = [d + (n – (j – I))]
и, поскольку 0< n – (j – I)<n, мы вступаем в противоречие с выбором числа n. Ч.т.д.
Предложение 2.1.
Если 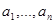 - такие элементы полугруппы, что
- такие элементы полугруппы, что  для любых i и j, то
для любых i и j, то
 , где
, где  - произвольная подстановка на множестве {1, 2, …,n}.
- произвольная подстановка на множестве {1, 2, …,n}.
Доказательство. При n = 2 утверждение теоремы справедливо по условию. Допустим, что теорема верна для n – 1 сомножителей. Если  (n) = n, то учитывая теорему: “ Произведение нескольких элементов полугруппы не зависит от расстановки скобок”, и индуктивное предположение, имеем
(n) = n, то учитывая теорему: “ Произведение нескольких элементов полугруппы не зависит от расстановки скобок”, и индуктивное предположение, имеем
 .
.
Если n =  (k), где k<n, то
(k), где k<n, то
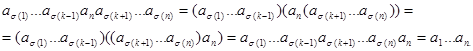
Ч.т.д.
Следствие.
Для любых элементов 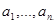 коммутативной полугруппы и любой подстановки
коммутативной полугруппы и любой подстановки  на множестве {1, 2, …,n} справедливо равенство
на множестве {1, 2, …,n} справедливо равенство

 .
.
Теорема 2. 2.
Если А = { 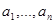 } – множество свободных образующих коммутативной полугруппы S, то S = {
} – множество свободных образующих коммутативной полугруппы S, то S = {  ,
, 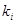 - неотрицательные целые числа, одновременно не равные нулю}, причём различные наборы показателей (
- неотрицательные целые числа, одновременно не равные нулю}, причём различные наборы показателей ( ) дают различные элементы S.
) дают различные элементы S.
Доказательство. По теореме 1.2. существует гомоморфное наложение  , при котором
, при котором  для всех
для всех 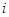 =1, 2, …,n. Значит, каждый элемент s
=1, 2, …,n. Значит, каждый элемент s 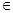 S имеет вид
S имеет вид  . Поскольку мультипликативная полугруппа {
. Поскольку мультипликативная полугруппа {  ,
, 
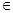
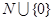 } изоморфны аддитивной полугруппе
} изоморфны аддитивной полугруппе  , то различные её элементы будут иметь различные наборы показателей. Ч.т.д.
, то различные её элементы будут иметь различные наборы показателей. Ч.т.д.
Упражнения
Для полугруппы слов W(X) верны следующие утверждения.
1. ef = gh  e = gu и h = uf либо g = eu и f = uh, для некоторого слова u (возможно непустое).
e = gu и h = uf либо g = eu и f = uh, для некоторого слова u (возможно непустое).
2. Из ef = fe  e = fk = kf для некоторого слова u либо f=eu=ue для некоторого слова u.
e = fk = kf для некоторого слова u либо f=eu=ue для некоторого слова u.
3. Если ef = fe,то следует слово h, для которого e = 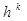 и f=
и f=  , где k, m – натуральные числа.
, где k, m – натуральные числа.
Докажем эти утверждения.
(1)  . Пусть
. Пусть  ,
,  и
и 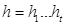 - слова в алфавите Х. По условию ef = gh. Если
- слова в алфавите Х. По условию ef = gh. Если 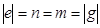 , то очевидно: e = g и f = h; в этом случае u =
, то очевидно: e = g и f = h; в этом случае u =  - пустое слово. Пусть n
- пустое слово. Пусть n 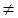 m. Будем считать, что n>m (случай m>n симметричен рассматриваемому). Имеем
m. Будем считать, что n>m (случай m>n симметричен рассматриваемому). Имеем
 =
=
= 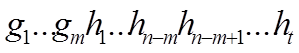
откуда e = gu и h = uf для слова u =  .
.
 . Пусть для определённости
. Пусть для определённости  и e = gu и h = uf. Тогда ef=(gu)f=g(uf)=gh. Ч.т.д.
и e = gu и h = uf. Тогда ef=(gu)f=g(uf)=gh. Ч.т.д.
(2) Это частный случай (1) при g = e и g = f.
(3) Пусть ef = fe. При  ясно, что e = f, то имеем e=f=h=
ясно, что e = f, то имеем e=f=h=  . Далее доказательство проведём индукцией по числу n=max (
. Далее доказательство проведём индукцией по числу n=max (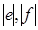 ). Можно считать, что n = 2 имеем
). Можно считать, что n = 2 имеем 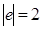 и
и  =1, то есть е=ab и f=c, где a, b, c
=1, то есть е=ab и f=c, где a, b, c 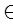 X. Тогда ef = abc и fe = cab. Поскольку ef = fe, то a = c, b = a, c = b, или a = b = c. Значит, e =
X. Тогда ef = abc и fe = cab. Поскольку ef = fe, то a = c, b = a, c = b, или a = b = c. Значит, e = 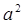 и f =
и f =  .
.
Предположим, что для всех натуральных чисел < n утверждение верно. Поскольку ef = fe, то в силу (2) e = fu = uf, где max ( )< n. По индуктивному предположению существует слово h, для которого f =
)< n. По индуктивному предположению существует слово h, для которого f = 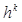 и u =
и u =  . Получаем f =
. Получаем f = 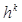 и e = f =
и e = f = 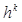
 =
= 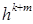 .Ч.т.д.
.Ч.т.д.
Теорема 3.1.
Слово и 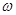 - слово свободно от перекрытий тогда и только тогда, когда оно является сильно бескубным.
- слово свободно от перекрытий тогда и только тогда, когда оно является сильно бескубным.
Доказательство. Пусть w не свободно от перекрытий. Тогда w найдется подслово xy = zx, такое, что имеет место 
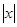 . Пусть а – первая буква слова z. По нашему предположению, x = zx
. Пусть а – первая буква слова z. По нашему предположению, x = zx 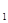 , где первой буквой слова x
, где первой буквой слова x 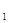 также будет а. Следовательно, zza – подслово w и w не является сильно бескубеым.
также будет а. Следовательно, zza – подслово w и w не является сильно бескубеым.
Наоборот, предположим, что w не является сильно бескубным. Тогда в w найдётся слово z 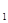 z
z 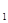 a, где а – первая буква z
a, где а – первая буква z 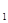 . Пологая z
. Пологая z 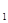 =аz
=аz 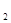 мы видим, что х = а z
мы видим, что х = а z 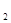 а, y = z
а, y = z 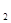 а, z = а z
а, z = а z 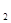 . Тогда xy = zx – подслово w, и, кроме того, выполняется
. Тогда xy = zx – подслово w, и, кроме того, выполняется 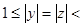
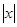 . Отсюда следует, что w не свободно от перекрытий. Ч.т.д.
. Отсюда следует, что w не свободно от перекрытий. Ч.т.д.
Теорема 3.2.
Ни одно слово, имеющее длину более 3, над алфавитом А из двух букв не является бесквадратным. Следовательно, над алфавиотм А не существует бесквадратных 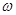 - слов.
- слов.
Доказательство. Пусть А состоит из букв a и b. Существуют только 2 бесквадратных слова
аbа и bаb, (*)
так как все другие слова указанной длины:
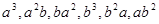
содержит в качестве подслова либо 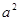 , либо
, либо 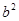 . С другой стороны, каким бы способом ни была приписана буква к любому слову из (*), результирующее слово в каждом случае будет содержать в качестве подслова одно из слов
. С другой стороны, каким бы способом ни была приписана буква к любому слову из (*), результирующее слово в каждом случае будет содержать в качестве подслова одно из слов 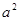 ,
, 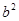 ,
,  и, следовательно, не будет бесквадратным.Ч.т.д.
и, следовательно, не будет бесквадратным.Ч.т.д.
Теоремя 3.3.
Ни 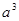 , ни
, ни 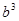 не входят в качестве подслова в
не входят в качестве подслова в 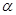 . Ни ababa, ни babab не входят в качестве подслова в
. Ни ababa, ни babab не входят в качестве подслова в 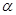 . Следовательно, любое подслово х
. Следовательно, любое подслово х 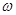 - слова
- слова 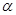
 , такое, что
, такое, что 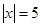 , содержит в качестве подслова либо
, содержит в качестве подслова либо 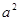 , либо
, либо 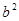 .
.
Доказательство. Докажем первое утверждение. Если слово 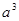 или
или 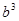 входит в качестве подслова в
входит в качестве подслова в 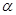 , то оно входит в качестве подслова в некоторое w
, то оно входит в качестве подслова в некоторое w  . Но это не возможно, так как w
. Но это не возможно, так как w 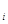 = h(w
= h(w 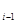 ) и, следовательно, w
) и, следовательно, w 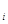 получено приписыванием слов ab и ba в некотором порядке.
получено приписыванием слов ab и ba в некотором порядке.
Докажем второе утверждение. Предположим, что ababa входит в качестве подслова в 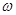 - слова
- слова 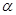 , начиная с j-й его буквы. Тогда используя
, начиная с j-й его буквы. Тогда используя 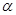 =
= 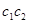 …, запишем
…, запишем
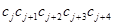 = ababa. (**)
= ababa. (**)
Выберем настолько большое j что 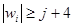 . Тогда вхождения (**) целиком лежит в w
. Тогда вхождения (**) целиком лежит в w 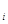 .Ещё раз используя соотношение w
.Ещё раз используя соотношение w 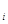 = h(w
= h(w 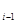 ), заключаем, что в w
), заключаем, что в w 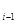 в качестве подслова входит либо
в качестве подслова входит либо 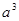 , либо
, либо 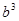 в зависимости от того, является ли j в (**) нечетным или четным. Но это не возможно в силу доказанного выше первого утверждения. Аналогично и для babab не входит в
в зависимости от того, является ли j в (**) нечетным или четным. Но это не возможно в силу доказанного выше первого утверждения. Аналогично и для babab не входит в 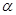 .
.
Наконец, последнее утверждение является следствием второго, так как, за исключением слов ababa и babab, любое слово длины 5 над {a,b} содержит в качестве подслова либо 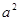 , либо
, либо 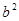 . Ч.т.д.
. Ч.т.д.
Теорема 3.4.
Предположим, что 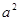 или
или 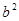 входит в качестве подслова в
входит в качестве подслова в 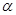 , начиная с j-й; тогда j четно.
, начиная с j-й; тогда j четно.
Доказательство. Используя обозначения предыдущей теоремы, предположим, что  есть
есть 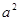 или
или 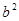 . Вновь выбираем такое i, что
. Вновь выбираем такое i, что 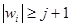 , и применяем соотношение w
, и применяем соотношение w 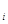 = h(w
= h(w 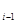 ). В силу этого соотношения, если j нечетно, то
). В силу этого соотношения, если j нечетно, то  есть либо h(a), либо h(b). Так как ни h(a), ни h(b) не есть
есть либо h(a), либо h(b). Так как ни h(a), ни h(b) не есть 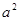 или
или 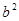 .Ч.т.д.
.Ч.т.д.
Литература
1. Курош А.Т. Лекции по общей алгебре. – М.: Наука, 1973.
2. Лаллеман Ж. Полугруппы и комбинаторные приложения. – М.: Мир, 1985.
3. Саломаа А. Жемчужины теории формальных языков. – М.: Мир, 1986.
4. Скорняков Л.А. Элементы алгебры. – М.: Наука, 1986.
Содержание
Введение------------------------------------------------------------------- 3
1. Понятие свободной полугруппы------------------------- 4
1.1. Слова------------------------------------------------------------ 4
1.2. Понятие свободной полугруппы-------------------------- 5
2. Применение--------------------------------------------------- 9
2.1. Циклические (моногенные) полугруппы--------------- 9
2.2. Сводные коммутативные полугруппы------------------ 12
2.3. Упражнения-------------------------------------------------- 13
3. Обзор результатов по проблеме Туэ-------------------- 15
Литература-----------------------------------------------------------
Введение
Дипломная работа посвящена теории свободных полугрупп. Свободные алгебраические объекты играют важную роль в общей алгебре, поскольку любая алгебраическая структура является гомоморфным образом свободной алгебраической структуры того же типа.
В теории полугрупп свободные объекты описываются конструктивно, именно как полугруппы слов над некоторым алфавитом. Поэтому большое место в работе уделено рассмотрению свойств полугрупп слов. Эти свойства носят, как правило, комбинаторный характер.
Кроме того, в работе изучаются и абстрактные свойства свободных полугрупп и некоторых связанных с ним полугрупп.
В первом параграфе вводятся основные понятия и доказательства теорем о существовании и единственности свободных полугрупп с множеством образующих данной мощности.
Второй параграф посвящён двум применениям свободных полугрупп:
1) описание циклических полугрупп;
2) свободной коммутативной полугруппе.
Там же доказываются некоторые комбинаторные свойства слов над произвольным алфавитом.
В третьем параграфе даётся обзор проблематики Туэ о существовании бесквадратных и бескубных слов произвольной длины над различными алфавитами.
В дипломной работе используются книги [1 - 4] из приведённого списка библиографии.
Понятие свободной подгруппы
Слова
Алфавит А – это непустое конечное множество. Буквы (символы)- элементы алфавита А. Слово над алфавитом А – это конечная цепочка, состоящая из нуля или более букв из А, причем одна и та же буква может входить несколько раз. Цепочка, состоящая из нулевого количества букв, называется пустым словом и обозначается 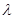 . Таким образом
. Таким образом 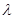 , 0, 1, 010, 1111 суть слова над алфавитом А ={0, 1}. Множество всех слов над алфавитом А обозначается W(A), а множество всех непустых слов обозначается Z(A).
, 0, 1, 010, 1111 суть слова над алфавитом А ={0, 1}. Множество всех слов над алфавитом А обозначается W(A), а множество всех непустых слов обозначается Z(A).
Если u и v – слова над алфавитом А, то их катенация xy (результат приписывания) – тоже слово над А:  и
и 

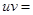
 . Катенация является ассоциативной операцией, и пустое множество служит единицей по отношению к ней: x
. Катенация является ассоциативной операцией, и пустое множество служит единицей по отношению к ней: x 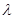 =
= 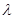 x=
x= 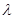 для всех x. Если х – слово, а i – натуральное число, то
для всех x. Если х – слово, а i – натуральное число, то 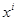 обозначает слово, полученное катенацией i слов, каждое из которых есть х.
обозначает слово, полученное катенацией i слов, каждое из которых есть х.
 Длина слова х, обозначается
Длина слова х, обозначается  , есть число букв в х, причем каждая буква считается столько раз, сколько раз она входит в х. Опять по определению
, есть число букв в х, причем каждая буква считается столько раз, сколько раз она входит в х. Опять по определению 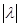 =0. Функция длины обладает некоторыми свойствами логарифма: для всех слов х, у и неотрицательных некоторых i
=0. Функция длины обладает некоторыми свойствами логарифма: для всех слов х, у и неотрицательных некоторых i
 ,
, 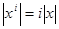 .
.
В теории языков важнейшей операцией является операция морфизма. Морфизмом называется отображение h: W(A) 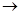 M(A), где W(A) и M(A) –множества всех слов удовлетворяющие условию h(xy)=h(x)h(y) для всех слов х,у.
M(A), где W(A) и M(A) –множества всех слов удовлетворяющие условию h(xy)=h(x)h(y) для всех слов х,у.
Понятие свободной полугруппы
Пусть S – полугруппа, а Х – ее непустое подмножество. Пересечение Т всех подполугрупп полугруппы S, содержащих Х, называется подполугруппой, порожденной множеством Х. Существовавние полугруппы Т вытекает из следующего простого факта: Непустое пересечение любого множества подполугрупп является подполугруппой.
Доказательство. Пусть Т – пересечение некоторого множества подполугрупп. Если х, у принадлежат Т, то х и у лежат в каждой из подполугрупп рассматриваемого множества. Но тогда в каждой из них лежит и произведение ху, а значит ху принадлежит Т. Ч.т.д.
Поэтому подполугруппы, содержащие множество Х существуют, например сама S, и пересечение их непусто (все они содержат Х). Значит Т – это наименьшая среди подполугрупп полугруппа S, содержащая Х. Если эта наименьшая подполугруппа совпадает с S, то говорят, что полугруппа S порождается множеством Х.
Полугруппа S=S(Х) называется свободной полугруппой со свободным порождающим множеством Х, если:
(1) S порождается множеством Х;
(2) для любого отображения 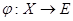 , где Е – произвольная полугруппа, существует гомоморфизм
, где Е – произвольная полугруппа, существует гомоморфизм  такой, что
такой, что
 для любых х
для любых х  Х.
Х.
Теорема 1.1. (существование свободной полугруппы).
W=W(x) – свободная полугруппа со свободно порождающим множеством Х.
Доказательство. Оба свойства (1) и (2) свободной полугруппы проверим индукцией по длине 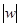 слов
слов 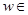 W.
W.
(1) Пусть Т – подполугруппа полугруппы W, порожденная множеством Х. Тогда любое слово w принадлежащее W, лежит в Т. Действительно, если 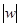 =1, то w принадлежит Х и подмножество Т. Если
=1, то w принадлежит Х и подмножество Т. Если 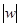 >1, то w=w’x, где
>1, то w=w’x, где  <
< 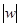 и х принадлежит Х. следовательно, w’, x принадлежит Т по предположению индукции. Так как Т - подполугруппа, а w – произведение двух элементов w’ и х, то w принадлежит Т. Поэтому W подмножество Т. Обратное включение очевидно. Итак, T=W.
и х принадлежит Х. следовательно, w’, x принадлежит Т по предположению индукции. Так как Т - подполугруппа, а w – произведение двух элементов w’ и х, то w принадлежит Т. Поэтому W подмножество Т. Обратное включение очевидно. Итак, T=W.
(2). Пусть 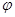 - произвольное отображение множества Х в некоторую полугруппу Е с операцией
- произвольное отображение множества Х в некоторую полугруппу Е с операцией 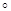 . Определим элемент
. Определим элемент  полугруппы Е индукцией по
полугруппы Е индукцией по 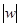 . Если
. Если 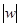 =1,w принадлежит Х и мы положим
=1,w принадлежит Х и мы положим
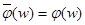 (*)
(*)
Если 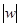 >1, то w=w’x где
>1, то w=w’x где  <
< 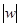 и х принадлежит Х. Тогда
и х принадлежит Х. Тогда 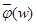 и
и 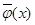 уже определены. Положим
уже определены. Положим
 (**)
(**)
Покажем, что отображение 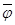 : W
: W 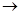 Е является гомоморфизмом, то есть что
Е является гомоморфизмом, то есть что 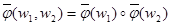 для любых
для любых 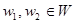 .
.
Проведем индукцию по длине второго сомножителя  . Если
. Если 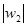 =1, то доказываемое следует из равенства (**). Если
=1, то доказываемое следует из равенства (**). Если 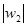 >1, то
>1, то  =
=  ’ х, где
’ х, где  <
< 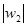 и х принадлежит Х. Поэтому, учитывая (**) и индуктивное предположение получаем:
и х принадлежит Х. Поэтому, учитывая (**) и индуктивное предположение получаем:

Кроме того, если х принадлежит Х, то  в силу равенства (*). Итак, условия (1) и (2) выполнены. Ч.т.д.
в силу равенства (*). Итак, условия (1) и (2) выполнены. Ч.т.д.
Теорема 1.2. (свойство универсальности свободной полугруппы).
Для всякой полугруппы Е найдутся свободная полугруппа S и гомоморфное наложение 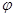 : S
: S 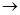 Е.
Е.
Доказательство. Пусть S – свободная полугруппа со свободно порождающим множеством Е. В силу свойства (2) из определения свободной полугруппы, тождественное отображение множества Е на себя продолжается до гомоморфизма 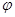 : S
: S 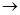 Е, который в данном случае оказался наложением. Ч.т.д.
Е, который в данном случае оказался наложением. Ч.т.д.
Теорема 1.3. (о единственности свободной полугруппы).
Если S=S(x) – свободная полугруппа со свободно порождающим множеством Х, то существует изоморфизм 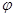 полугруппы S на полугруппу W=W(x) слов в алфавите Х, причем
полугруппы S на полугруппу W=W(x) слов в алфавите Х, причем 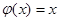 , для всех х принадлежащих Х.
, для всех х принадлежащих Х.
Доказательство. По Т1. и свойству (2) из определения свободной полугруппы, тождественное отображение множества Х на себя продолжается до гомоморфизмов 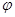 : S
: S 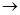 W и
W и 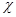 : W
: W 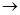 S, причем
S, причем 
 , для любых х принадлежащих Х. Таким образом Х
, для любых х принадлежащих Х. Таким образом Х  и Х
и Х 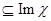 .
.
По теореме “Если 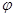 : А
: А 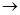 В – гомоморфизм полугруппы, то
В – гомоморфизм полугруппы, то 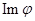 - подполугруппа В ”
- подполугруппа В ”  и свойству (1)
и свойству (1) 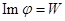 и
и  , то есть как
, то есть как 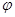 ,так и
,так и  оказываются наложениями. Более того, поскольку
оказываются наложениями. Более того, поскольку 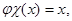 для всех х принадлежащих Х, не трудно заметить, что
для всех х принадлежащих Х, не трудно заметить, что 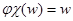 для любого слова w в алфавите Х, то есть
для любого слова w в алфавите Х, то есть  . Если
. Если 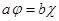 некоторых a,b принадлежащих W, то
некоторых a,b принадлежащих W, то

Следовательно 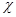 - вложение, а значит и изморфизм. Ч.т.д.
- вложение, а значит и изморфизм. Ч.т.д.
Теорема 1.4. (об изоморфности свободных полугрупп)
Свободные полугруппы S(X) и S(Y) изоморфны 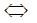 равномощны множества X и Y.
равномощны множества X и Y.
Доказательство. Необходимость. По теореме 1.3. имеем S(X)  W(X) и S(Y)
W(X) и S(Y)  W(Y). В полугруппе W(X) неразложимыми элементами будут в точности буквы алфавита Х.
W(Y). В полугруппе W(X) неразложимыми элементами будут в точности буквы алфавита Х.
Пусть S(X)  S(Y). Тогда W(X)
S(Y). Тогда W(X)  W(Y). Поскольку при изоморфизме полугрупп сохраняются все алгебраические свойства, то неразложимые элементы перейдут в неразложимые. Значит между X и Y будет установлено взаимно однозначное соответствие.
W(Y). Поскольку при изоморфизме полугрупп сохраняются все алгебраические свойства, то неразложимые элементы перейдут в неразложимые. Значит между X и Y будет установлено взаимно однозначное соответствие.
Достаточность. Пусть X равномощно Y, то есть существует биекция f множества X на множество Y. Тогда f продолжается до гомоморфизма  , а обратное
, а обратное 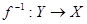 продолжается до гомоморфизма
продолжается до гомоморфизма 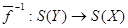 .
.
Легко видеть, что гомоморфизмы 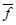 и
и  взаимно обратны
взаимно обратны 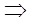
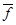 - это изоморфизм свободных полугрупп S(X) и S(Y).Ч.т.д.
- это изоморфизм свободных полугрупп S(X) и S(Y).Ч.т.д.
2. Применения



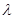 . Таким образом
. Таким образом  и
и 

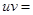
 . Катенация является ассоциативной операцией, и пустое множество служит единицей по отношению к ней: x
. Катенация является ассоциативной операцией, и пустое множество служит единицей по отношению к ней: x 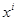 обозначает слово, полученное катенацией i слов, каждое из которых есть х.
обозначает слово, полученное катенацией i слов, каждое из которых есть х. Длина слова х, обозначается
Длина слова х, обозначается  , есть число букв в х, причем каждая буква считается столько раз, сколько раз она входит в х. Опять по определению
, есть число букв в х, причем каждая буква считается столько раз, сколько раз она входит в х. Опять по определению 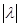 =0. Функция длины обладает некоторыми свойствами логарифма: для всех слов х, у и неотрицательных некоторых i
=0. Функция длины обладает некоторыми свойствами логарифма: для всех слов х, у и неотрицательных некоторых i ,
, 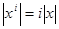 .
.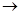 M(A), где W(A) и M(A) –множества всех слов удовлетворяющие условию h(xy)=h(x)h(y) для всех слов х,у.
M(A), где W(A) и M(A) –множества всех слов удовлетворяющие условию h(xy)=h(x)h(y) для всех слов х,у. .
.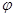 оказывается наложением. В силу теоремы: “
оказывается наложением. В силу теоремы: “ 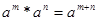 для всех m, n > 0.”
для всех m, n > 0.” 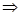
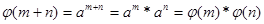 ,
, - гомоморфное наложение полугрупп и
- гомоморфное наложение полугрупп и 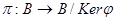 - естественный гомоморфизм, то существует изоморфизм
- естественный гомоморфизм, то существует изоморфизм  такой, что
такой, что  , вытекает, что В изоморфна факторполугруппе Р/
, вытекает, что В изоморфна факторполугруппе Р/  , где
, где 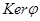 . Если все классы разбиения
. Если все классы разбиения  [d + I] при I= 1,2,…, n – 1. Докажем, что
[d + I] при I= 1,2,…, n – 1. Докажем, что . (**)
. (**) , получаем
, получаем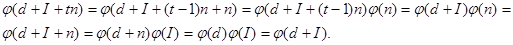
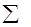 совпадает с разбиением
совпадает с разбиением  , различны. Но если [d + I] = = [d + j], то
, различны. Но если [d + I] = = [d + j], то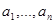 - такие элементы полугруппы, что
- такие элементы полугруппы, что  для любых i и j, то
для любых i и j, то , где
, где  - произвольная подстановка на множестве {1, 2, …,n}.
- произвольная подстановка на множестве {1, 2, …,n}. (n) = n, то учитывая теорему: “ Произведение нескольких элементов полугруппы не зависит от расстановки скобок”, и индуктивное предположение, имеем
(n) = n, то учитывая теорему: “ Произведение нескольких элементов полугруппы не зависит от расстановки скобок”, и индуктивное предположение, имеем .
. 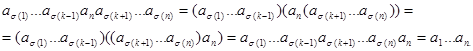
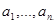 коммутативной полугруппы и любой подстановки
коммутативной полугруппы и любой подстановки  .
. ,
, 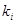 - неотрицательные целые числа, одновременно не равные нулю}, причём различные наборы показателей (
- неотрицательные целые числа, одновременно не равные нулю}, причём различные наборы показателей ( ) дают различные элементы S.
) дают различные элементы S. , при котором
, при котором  для всех
для всех 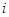 =1, 2, …,n. Значит, каждый элемент s
=1, 2, …,n. Значит, каждый элемент s 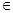 S имеет вид
S имеет вид  . Поскольку мультипликативная полугруппа {
. Поскольку мультипликативная полугруппа {  ,
, 
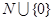 } изоморфны аддитивной полугруппе
} изоморфны аддитивной полугруппе  , то различные её элементы будут иметь различные наборы показателей. Ч.т.д.
, то различные её элементы будут иметь различные наборы показателей. Ч.т.д. e = gu и h = uf либо g = eu и f = uh, для некоторого слова u (возможно непустое).
e = gu и h = uf либо g = eu и f = uh, для некоторого слова u (возможно непустое).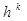 и f=
и f=  , где k, m – натуральные числа.
, где k, m – натуральные числа. . Пусть
. Пусть  ,
,  и
и 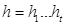 - слова в алфавите Х. По условию ef = gh. Если
- слова в алфавите Х. По условию ef = gh. Если 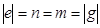 , то очевидно: e = g и f = h; в этом случае u =
, то очевидно: e = g и f = h; в этом случае u =  - пустое слово. Пусть n
- пустое слово. Пусть n 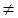 m. Будем считать, что n>m (случай m>n симметричен рассматриваемому). Имеем
m. Будем считать, что n>m (случай m>n симметричен рассматриваемому). Имеем =
=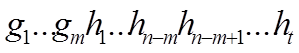
 .
. . Пусть для определённости
. Пусть для определённости  и e = gu и h = uf. Тогда ef=(gu)f=g(uf)=gh. Ч.т.д.
и e = gu и h = uf. Тогда ef=(gu)f=g(uf)=gh. Ч.т.д. ясно, что e = f, то имеем e=f=h=
ясно, что e = f, то имеем e=f=h=  . Далее доказательство проведём индукцией по числу n=max (
. Далее доказательство проведём индукцией по числу n=max (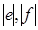 ). Можно считать, что n = 2 имеем
). Можно считать, что n = 2 имеем 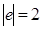 и
и  =1, то есть е=ab и f=c, где a, b, c
=1, то есть е=ab и f=c, где a, b, c 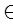 X. Тогда ef = abc и fe = cab. Поскольку ef = fe, то a = c, b = a, c = b, или a = b = c. Значит, e =
X. Тогда ef = abc и fe = cab. Поскольку ef = fe, то a = c, b = a, c = b, или a = b = c. Значит, e = 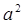 и f =
и f =  .
. )< n. По индуктивному предположению существует слово h, для которого f =
)< n. По индуктивному предположению существует слово h, для которого f = 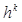 и u =
и u =  . Получаем f =
. Получаем f = 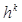 и e = f =
и e = f = 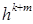 .Ч.т.д.
.Ч.т.д.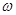 - слово свободно от перекрытий тогда и только тогда, когда оно является сильно бескубным.
- слово свободно от перекрытий тогда и только тогда, когда оно является сильно бескубным.
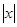 . Пусть а – первая буква слова z. По нашему предположению, x = zx
. Пусть а – первая буква слова z. По нашему предположению, x = zx 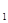 , где первой буквой слова x
, где первой буквой слова x 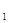 также будет а. Следовательно, zza – подслово w и w не является сильно бескубеым.
также будет а. Следовательно, zza – подслово w и w не является сильно бескубеым.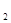 мы видим, что х = а z
мы видим, что х = а z 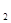 а, z = а z
а, z = а z 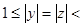
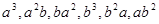
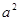 , либо
, либо 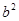 . С другой стороны, каким бы способом ни была приписана буква к любому слову из (*), результирующее слово в каждом случае будет содержать в качестве подслова одно из слов
. С другой стороны, каким бы способом ни была приписана буква к любому слову из (*), результирующее слово в каждом случае будет содержать в качестве подслова одно из слов 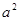 ,
,  и, следовательно, не будет бесквадратным.Ч.т.д.
и, следовательно, не будет бесквадратным.Ч.т.д.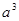 , ни
, ни 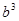 не входят в качестве подслова в
не входят в качестве подслова в 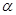 . Ни ababa, ни babab не входят в качестве подслова в
. Ни ababa, ни babab не входят в качестве подслова в 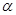
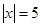 , содержит в качестве подслова либо
, содержит в качестве подслова либо 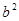 .
. . Но это не возможно, так как w
. Но это не возможно, так как w 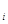 = h(w
= h(w 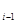 ) и, следовательно, w
) и, следовательно, w 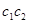 …, запишем
…, запишем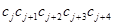 = ababa. (**)
= ababa. (**)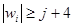 . Тогда вхождения (**) целиком лежит в w
. Тогда вхождения (**) целиком лежит в w 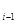 в качестве подслова входит либо
в качестве подслова входит либо  есть
есть 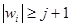 , и применяем соотношение w
, и применяем соотношение w 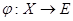 , где Е – произвольная полугруппа, существует гомоморфизм
, где Е – произвольная полугруппа, существует гомоморфизм  такой, что
такой, что для любых х
для любых х  Х.
Х.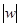 слов
слов 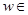 W.
W. <
< 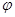 - произвольное отображение множества Х в некоторую полугруппу Е с операцией
- произвольное отображение множества Х в некоторую полугруппу Е с операцией 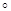 . Определим элемент
. Определим элемент  полугруппы Е индукцией по
полугруппы Е индукцией по 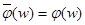 (*)
(*) <
< 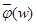 и
и 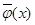 уже определены. Положим
уже определены. Положим (**)
(**)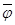 : W
: W 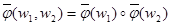 для любых
для любых 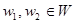 .
. . Если
. Если 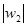 =1, то доказываемое следует из равенства (**). Если
=1, то доказываемое следует из равенства (**). Если  =
=  <
< 
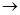 Е.
Е.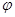 : S
: S 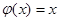 , для всех х принадлежащих Х.
, для всех х принадлежащих Х.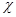 : W
: W 
 , для любых х принадлежащих Х. Таким образом Х
, для любых х принадлежащих Х. Таким образом Х  и Х
и Х 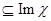 .
.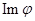 - подполугруппа В ”
- подполугруппа В ” 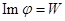 и
и  , то есть как
, то есть как  оказываются наложениями. Более того, поскольку
оказываются наложениями. Более того, поскольку 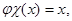 для всех х принадлежащих Х, не трудно заметить, что
для всех х принадлежащих Х, не трудно заметить, что 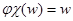 для любого слова w в алфавите Х, то есть
для любого слова w в алфавите Х, то есть  . Если
. Если 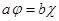 некоторых a,b принадлежащих W, то
некоторых a,b принадлежащих W, то
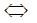 равномощны множества X и Y.
равномощны множества X и Y. W(X) и S(Y)
W(X) и S(Y)  , а обратное
, а обратное 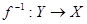 продолжается до гомоморфизма
продолжается до гомоморфизма 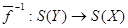 .
.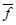 и
и  взаимно обратны
взаимно обратны 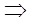
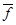 - это изоморфизм свободных полугрупп S(X) и S(Y).Ч.т.д.
- это изоморфизм свободных полугрупп S(X) и S(Y).Ч.т.д.


