Методическая разработка
на тему: «Производная и ее приложение»
по дисциплине «Математика»
План:
1. Введение.
2. Понятие производной.
3. Кинематический смысл производной.
4. Геометрический смысл производной.
5. Правило нахождения производной.
6. Правила и формулы дифференцирования.
7. Сложная функция и ее производная.
8. Самостоятельно
Введение
При изучении тех или иных процессов и явлений часто возникает задача определения скорости этих процессов. Ее решение приводит к понятию производной, являющемуся основным понятием дифференциального исчисления.
Метод дифференциального исчисления был создан в XVII и XVIII вв. С возникновением этого метода связаны имена двух великих математиков – И.Ньютона и Г.Лейбница.
Механическое истолкование производной было впервые дано И.Ньютоном. Оно заключается в следующем: скорость движения материальной точки в данный момент времени равна производной пути по времени.
Лейбниц пришел к открытию дифференциального исчисления при решении задачи о построении касательной к любой кривой, заданной уравнением.
Решение этой задачи имеет большое значение. Ведь скорость движущейся точки направлена по касательной к ее траектории, поэтому определение скорости снаряда на его траектории, скорости любой планеты на ее орбите сводится к определению направления касательной к кривой.
Понятие производной
Пусть  – некоторая функция, определенная на промежутке (a; b) и
– некоторая функция, определенная на промежутке (a; b) и  - некоторая фиксированная точка этого промежутка. Возьмем произвольное значение x из промежутка (a; b) и составим разность x -
- некоторая фиксированная точка этого промежутка. Возьмем произвольное значение x из промежутка (a; b) и составим разность x -  . Разность x -
. Разность x -  называют приращением независимой переменной (или приращением аргумента) функции
называют приращением независимой переменной (или приращением аргумента) функции  в точке
в точке  и обозначают
и обозначают 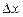 :
:
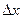 = x -
= x -  (1)
(1)
Приращением функции  в точке
в точке  называют разность между значением функции в точке
называют разность между значением функции в точке 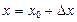 и значением функции в точке
и значением функции в точке  и обозначают
и обозначают 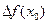 :
:
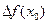 =
= 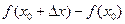 (2).
(2).
Т.к. точка  считается фиксированной, приращением функции
считается фиксированной, приращением функции 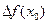 является функцией приращения аргумента
является функцией приращения аргумента 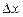 .
.
Составим отношение
 ,
,
которое также будет функцией приращения аргумента 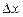 ; и рассмотрим предел этого выражения при
; и рассмотрим предел этого выражения при 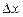 , стремящемся к нулю:
, стремящемся к нулю:
 .
.
Если этот предел существует, то говорят, что функция  имеет производную в точке
имеет производную в точке  , и пишут:
, и пишут:
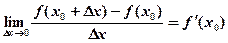 (3).
(3).
Число  называется производной функции в точке
называется производной функции в точке  .
.
Производная постоянной величины (константы)
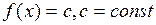

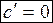
Производная переменной (аргумента)
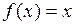


Производная алгебраической суммы функций
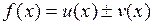
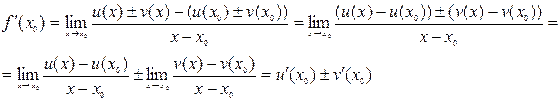

Производная произведения функций
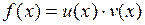

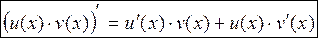
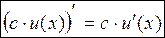
Производная частного функций

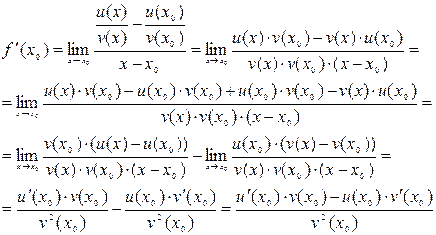
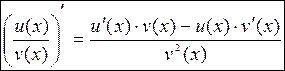
Формула дифференцирования показательной функции
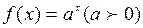
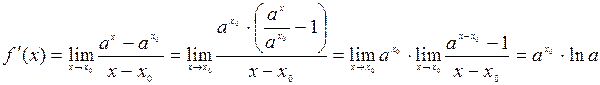
(Использовался известный предел 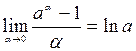 )
)
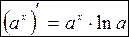
В случае 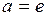 , применяя определение натурального логарифма, для числа е получаем формулу:
, применяя определение натурального логарифма, для числа е получаем формулу:

Формула дифференцирования тригонометрических функций
А) синуса
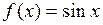
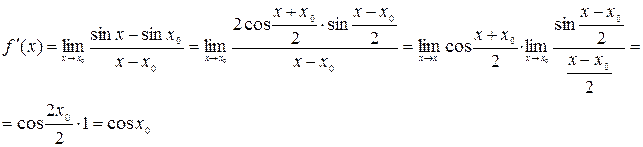
(применялась формула разности синусов и использовался первый замечательный предел: 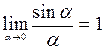 )
)
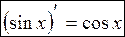
Б) косинуса
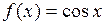
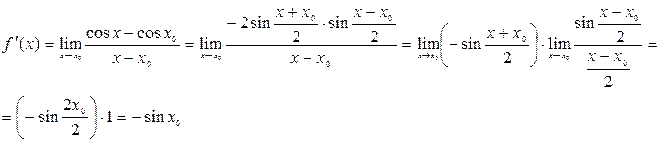
(применялась формула разности косинусов и использовался первый замечательный предел: 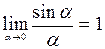 )
)
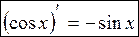
В) тангенса
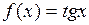 ,
, 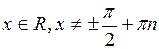
По определению, 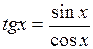 . Воспользуемся формулой производной частного функций и основным тригонометрическим тождеством:
. Воспользуемся формулой производной частного функций и основным тригонометрическим тождеством:
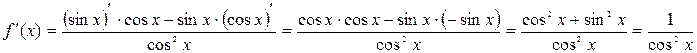
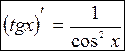
Г) котангенса
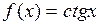 ,
, 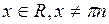
По определению, 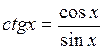 . Воспользуемся формулой производной частного функций и основным тригонометрическим тождеством:
. Воспользуемся формулой производной частного функций и основным тригонометрическим тождеством:
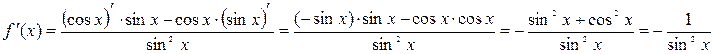
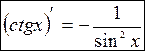
Для нахождения производных логарифмической и обратных тригонометрических функций понадобится теорема о производной обратной функции, так как данные функции являются обратными к показательной и тригонометрическим функциям соответственно.
А) арксинуса
Функция 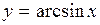 ,
, 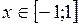 , является обратной к функции
, является обратной к функции 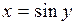 ,
, 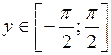 .
.
По правилу дифференцирования обратной функции
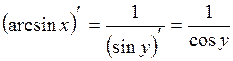 .
.
Выразим 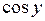 через
через 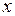 :
:
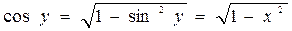 .
.
Под корнем следует брать знак «+», потому что 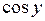 на промежутке
на промежутке 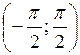 положителен.
положителен.
Таким образом,

Б) арккосинуса
Функция 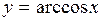 ,
, 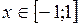 , является обратной к функции
, является обратной к функции 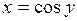 ,
, 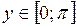 .
.
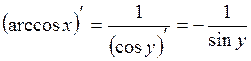
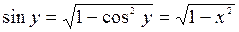
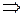
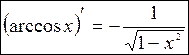
В) арктангенса
Функция 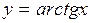 ,
, 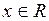 , является обратной к функции
, является обратной к функции 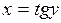 ,
, 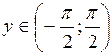 .
.
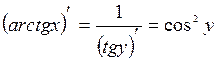
Используя основное тригонометрическое тождество, получаем следующее:
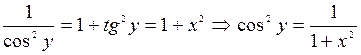
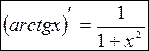
Г) арккотангенса
Функция 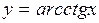 ,
, 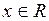 , является обратной к функции
, является обратной к функции 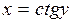 ,
, 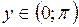 .
.
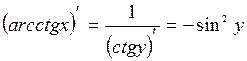
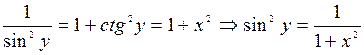
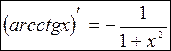
Методическая разработка
на тему: «Производная и ее приложение»
по дисциплине «Математика»
План:
1. Введение.
2. Понятие производной.
3. Кинематический смысл производной.
4. Геометрический смысл производной.
5. Правило нахождения производной.
6. Правила и формулы дифференцирования.
7. Сложная функция и ее производная.
8. Самостоятельно
Введение
При изучении тех или иных процессов и явлений часто возникает задача определения скорости этих процессов. Ее решение приводит к понятию производной, являющемуся основным понятием дифференциального исчисления.
Метод дифференциального исчисления был создан в XVII и XVIII вв. С возникновением этого метода связаны имена двух великих математиков – И.Ньютона и Г.Лейбница.
Механическое истолкование производной было впервые дано И.Ньютоном. Оно заключается в следующем: скорость движения материальной точки в данный момент времени равна производной пути по времени.
Лейбниц пришел к открытию дифференциального исчисления при решении задачи о построении касательной к любой кривой, заданной уравнением.
Решение этой задачи имеет большое значение. Ведь скорость движущейся точки направлена по касательной к ее траектории, поэтому определение скорости снаряда на его траектории, скорости любой планеты на ее орбите сводится к определению направления касательной к кривой.
Понятие производной
Пусть  – некоторая функция, определенная на промежутке (a; b) и
– некоторая функция, определенная на промежутке (a; b) и  - некоторая фиксированная точка этого промежутка. Возьмем произвольное значение x из промежутка (a; b) и составим разность x -
- некоторая фиксированная точка этого промежутка. Возьмем произвольное значение x из промежутка (a; b) и составим разность x -  . Разность x -
. Разность x -  называют приращением независимой переменной (или приращением аргумента) функции
называют приращением независимой переменной (или приращением аргумента) функции  в точке
в точке  и обозначают
и обозначают 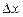 :
:
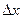 = x -
= x -  (1)
(1)
Приращением функции  в точке
в точке  называют разность между значением функции в точке
называют разность между значением функции в точке 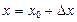 и значением функции в точке
и значением функции в точке  и обозначают
и обозначают 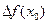 :
:
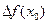 =
= 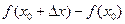 (2).
(2).
Т.к. точка  считается фиксированной, приращением функции
считается фиксированной, приращением функции 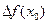 является функцией приращения аргумента
является функцией приращения аргумента 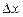 .
.
Составим отношение
 ,
,
которое также будет функцией приращения аргумента 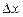 ; и рассмотрим предел этого выражения при
; и рассмотрим предел этого выражения при 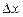 , стремящемся к нулю:
, стремящемся к нулю:
 .
.
Если этот предел существует, то говорят, что функция  имеет производную в точке
имеет производную в точке  , и пишут:
, и пишут:
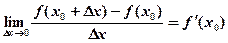 (3).
(3).
Число  называется производной функции в точке
называется производной функции в точке  .
.
Нахождение производной называется дифференцированием функции.
Если существует предел (3), также говорят, что функция  дифференцируема в точке
дифференцируема в точке  .
.
Если функция  дифференцируема в каждой точке промежутка (a; b), то говорят, что она дифференцируема в промежутке (a; b).
дифференцируема в каждой точке промежутка (a; b), то говорят, что она дифференцируема в промежутке (a; b).
Производная функции  , дифференцируемой в промежутке (a; b), сама является функцией x.
, дифференцируемой в промежутке (a; b), сама является функцией x.
Физический смысл производной
Пусть материальная точка движется по прямой под действием некоторых сил, не меняя направления своего движения, и пусть S(t) - расстояние, пройденное точкой от некоторого момента времени, который принят за нулевой, до момента t. Выберем какой-либо момент времени  и рассмотрим промежуток времени
и рассмотрим промежуток времени  от момента
от момента  до момента
до момента  . За этот промежуток времени точка пройдет некоторый путь, который обозначим
. За этот промежуток времени точка пройдет некоторый путь, который обозначим 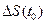 . Этот путь есть функция
. Этот путь есть функция  . По известному из физики определению отношение
. По известному из физики определению отношение 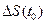 /
/  есть средняя скорость движения точки за время
есть средняя скорость движения точки за время  . Будем рассматривать все меньшие и меньшие промежутки
. Будем рассматривать все меньшие и меньшие промежутки  , устремляя
, устремляя  к нулю.
к нулю.
Предел 

 называется мгновенной скоростью точки в момент времени
называется мгновенной скоростью точки в момент времени  .
.
Производная характеризует мгновенную скорость прямолинейного движения. Однако этим не исчерпывается использование производной. Производная имеет самые широкие практические применения в вопросах физики, химии, геометрии и т.д. При изучении неравномерно меняющихся величин скорость их изменения всегда выражается с помощью производной (мгновенная скорость распада радиоактивных веществ, мгновенная мощность, коэффициент сжатия жидкости при данном давлении, угловая скорость в данный момент времени, сила тока, теплоемкость при данной температуре).
Понятие скорости, заимствованное из физики, удобно при исследовании поведения любой функции. Какую бы зависимость ни выражала функция  , отношение
, отношение  есть средняя скорость изменения функции
есть средняя скорость изменения функции  относительно изменения аргумента х, а
относительно изменения аргумента х, а 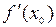 - мгновенная скорость изменения функции
- мгновенная скорость изменения функции  при некотором значении
при некотором значении  .
.



 – некоторая функция, определенная на промежутке (a; b) и
– некоторая функция, определенная на промежутке (a; b) и  - некоторая фиксированная точка этого промежутка. Возьмем произвольное значение x из промежутка (a; b) и составим разность x -
- некоторая фиксированная точка этого промежутка. Возьмем произвольное значение x из промежутка (a; b) и составим разность x - 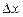 :
: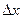 = x -
= x - 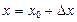 и значением функции в точке
и значением функции в точке 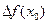 :
: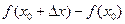 (2).
(2). ,
, .
. 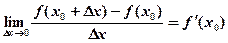 (3).
(3). называется производной функции в точке
называется производной функции в точке 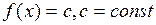

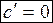
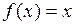


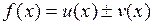
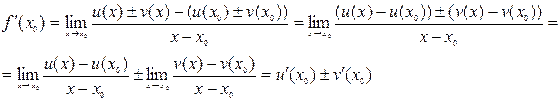

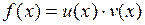

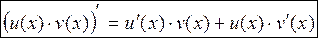
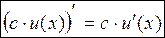

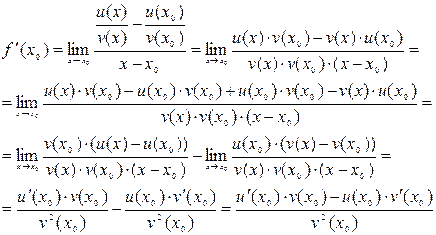
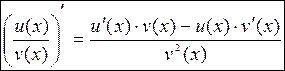
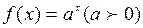
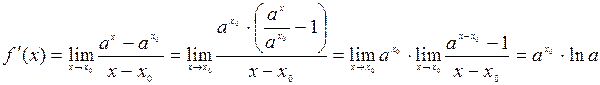
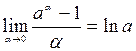 )
)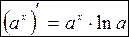
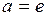 , применяя определение натурального логарифма, для числа е получаем формулу:
, применяя определение натурального логарифма, для числа е получаем формулу:
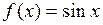
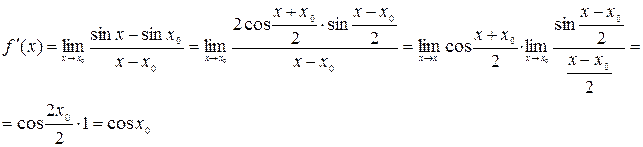
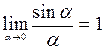 )
)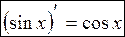
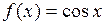
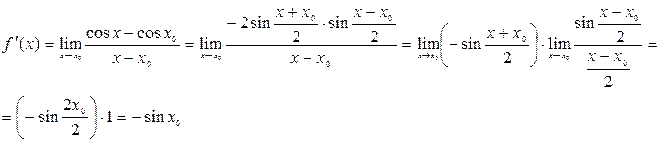
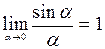 )
)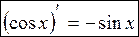
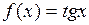 ,
, 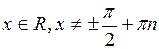
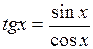 . Воспользуемся формулой производной частного функций и основным тригонометрическим тождеством:
. Воспользуемся формулой производной частного функций и основным тригонометрическим тождеством: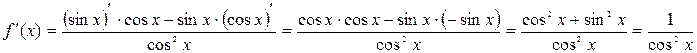
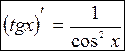
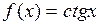 ,
, 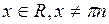
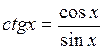 . Воспользуемся формулой производной частного функций и основным тригонометрическим тождеством:
. Воспользуемся формулой производной частного функций и основным тригонометрическим тождеством: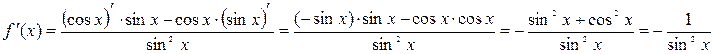
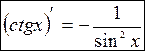
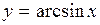 ,
, 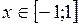 , является обратной к функции
, является обратной к функции 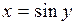 ,
, 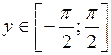 .
.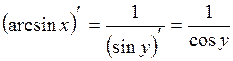 .
.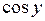 через
через 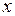 :
: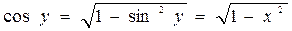 .
.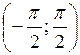 положителен.
положителен.
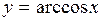 ,
, 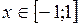 , является обратной к функции
, является обратной к функции 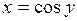 ,
, 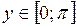 .
.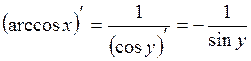
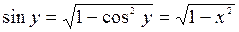
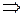
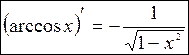
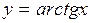 ,
, 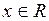 , является обратной к функции
, является обратной к функции 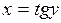 ,
, 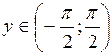 .
.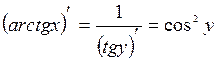
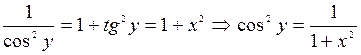
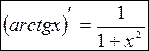
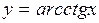 ,
, 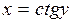 ,
, 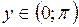 .
.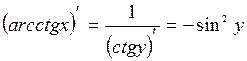
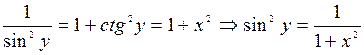
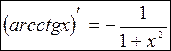
 и рассмотрим промежуток времени
и рассмотрим промежуток времени  от момента
от момента  до момента
до момента  . За этот промежуток времени точка пройдет некоторый путь, который обозначим
. За этот промежуток времени точка пройдет некоторый путь, который обозначим 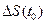 . Этот путь есть функция
. Этот путь есть функция 
 называется мгновенной скоростью точки в момент времени
называется мгновенной скоростью точки в момент времени  , отношение
, отношение  есть средняя скорость изменения функции
есть средняя скорость изменения функции  относительно изменения аргумента х, а
относительно изменения аргумента х, а 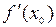 - мгновенная скорость изменения функции
- мгновенная скорость изменения функции  .
.


