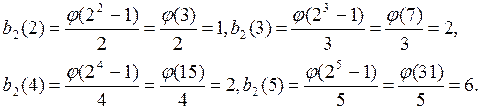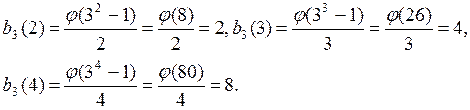Определение 1. Пусть p – простое число, q – степень простого числа p, n – натуральное число, f – нормированный многочлен степеyи n с коэффициентами из поля Fp, f (0) ¹ 0. Порядком многочлена f называется такое наименьшее натуральное число d, что
f | (x d - 1).
Порядок многочлена обозначаем через ord f.
Пример 1. Так как x 3 – 1 = (x 2 + x + 1)(x + 1), а x 2 – 1, x – 1 не делятся на x 2 + x + 1, то порядок многочлена x 2 + x + 1 над полем F 2 равен 3.
Так как
x 7 – 1 = (x + 1)(x 6 + x 5 + x 4 + x 3 + x 2 + x + 1) = (x + 1)(x 3 + x 2 + 1)(x 3 + x + 1),
а многочлены x – 1, x 2 – 1, x 3 – 1, x 4 – 1, x 5 – 1, x 6 – 1 не делятся на x 3 + x + 1, то порядок многочлена x 3 + x + 1 над полем F 2 равен 7.
Так как
(x - 1)(x + 3) (x + 5) = x 3 + 7 x 2 + 7 x – 15 = x 3 - 1,
а многочлены x – 1, x 2 – 1 не делятся на x + 5, то порядок многочлена x + 5 над полем F 7 равен 3.
Теорема 1. Если f – нормированный многочлен степени n над полем Fp, f (0) ¹ 0, то
1 £ ord f £ pn -1.
Доказательство. Так как deg f = n, то число возможных остатков от деления многочленов над полем Fp на многочлен f равно pn, в том числе pn – 1 отличных от нуля. В ряду из pn многочленов

каждый из которых не делится на f, заведомо найдутся такие два многочлена xi, xj, где i > j, что f делит xi - xj = xj (xi - j - 1). Так как многочлены x и f по условию взаимно простые, то f делит xi - j – 1, и при этом 1 £ i - j £ pn – 1. Отсюда следует, что 1 £ ord f £ pn -1.ÿ
Теорема 2. Если f – неприводимый и нормированный над Fp многочлен с корнем q ¹ 0, то
ord f = ord q.
Доказательство. Пусть a = ord f, b = ord q. Имеем f |(x a - 1). Поэтому qa - 1= 0. Так как b = ord q наименьшее натуральное число с этим свойством, то b £. a.
С другой стороны, qb - 1= 0. Таким образом, многочлены f и x b - 1 имеют общий корень q. Так как то f |(x b - 1) и a £. b. Отсюда b = a.ÿ
Теорема 3. Если f – неприводимый над Fp многочлен степени n и d = ord f, то
d | (pn - 1).
Доказательство. Пусть q - один из корней многочлена f в его поле разложения H. Так как многочлен f имеет порядок, то q ¹ 0, и поэтому q - элемент мультипликативной группы H * порядка pn - 1. Так как порядок элемента делит порядок группы, то получаем, что ord q | (pn - 1).ÿ
Имеем f |(x a - 1). Поэтому qa - 1= 0. Так как b = ord q наименьшее натуральное число с этим свойством, то b £. a.
С другой стороны, qb - 1= 0. Таким образом, многочлены f и x b - 1 имеют общий корень q. Так как многочлен f неприводим на полем Fp, то f |(x b - 1) и a £. b. Отсюда b = a.ÿ
Определение 2. Неприводимый на полем Fp многочлен f называется примитивным над полем Fp, если
ord а = pn - 1.
Через bp (n) обозначим число всех примитивных над полем Fp многочленов степени n.
Теорема 4. Число всех примитивных над полем Fp многочленов степени n равно
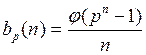 . (1)
. (1)
Доказательство. Из теоремы 2 следует, что каждый корень примитивного над Fp многочлена степени n есть примитивный элемент поля Fq, где q = pn. Верно и обратное: каждый примитивный элемент поля Fq – корень какого-нибудь примитивного над полем Fp многочлена степени n. Далее неприводимые над полем Fp и нормированные многочлены f и g тогда и только тогда имеют общий корень в некотором расширении поля Fp, когда они совпадают. По свойству порядка, число элементов поля Fq порядка q – 1 равно j(pn - 1). Так как различные нормированные неприводимые над полем Fp многочлены попарно взаимно простые, то они имеют различные корни. Так как каждый неприводимый над Fp многочлен степени n имеет n различных корней, то получаем, что 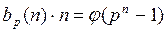 . Отсюда следует формула (1).ÿ
. Отсюда следует формула (1).ÿ
Пример 2. 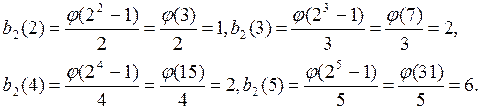
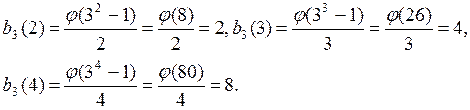




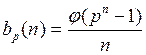 . (1)
. (1)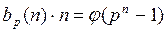 . Отсюда следует формула (1).ÿ
. Отсюда следует формула (1).ÿ