Определение 1. Многочлен f Î F [ x ] называется нормированным, если старший член многочлена f равен 1.
Определение 2. Многочлен f Î F [ x ] степени большей нуля называется приводимым над полем F, если его можно представить в виде произведения двух многочленов степени > 0 c коэффициентами из поля F.
Определение 3. Многочлен f Î F [ x ] степени большей нуля называется неприводимым над полем F, если его нельзя представить в виде произведения двух многочленов степени > 0 c коэффициентами из поля F.
Обозначим через aq (n) число нормированных неприводимых многочленов (ННМ) степени n с коэффициентами из поля Fq.
Пример 1. Нормированные многочлены первой степени над Z 2 есть
x, x +1 (1)
и оба эти многочлена неприводимы над Z 2. Следовательно, a 2(1) = 2.
2. Нормированные многочлены второй степени над Z 2 есть
x 2, x 2 + x, x 2 +1, x 2 + x +1. (2)
Первый, второй и третий многочлены из (2) приводимы над Z 2, например, x 2 +1 = x 2 + 2 x +1 = (x +1)2, а последний многочлен не делится ни на один из многочленов (1) и поэтому неприводим над Z 2. Следовательно, a 2(2) = 1.
3. Нормированные многочлены третьей степени над Z 2 есть
x 3, x 3 + x, x 3 +1, x 3 + x +1, x 3 + x 2, x 3 + x 2 + x, x 3 + x 2 +1, x 3 + x 2 + x +1. (3)
Первый, второй и третий, пятый, шестой, восьмой многочлены из (3) приводимы над Z 2, четвертый и седьмой последний многочлен не делится ни на один из многочленов (1) и поэтому неприводимы над Z 2. Следовательно, a 2(3) = 2.
Теорема 1. Поле разложения H многочлена
 (4)
(4)
над полем Fp есть конечное расширение поля Fp степени n.
Доказательство. Поле H – конечное расширение поля Fp, так как любое конечное поле является конечным расширением любого своего под поля. Пусть [ H, Fp ] = k. Тогда число элементов поля H равно pk, а другой стороны, поле разложения H многочлена (4) имеет элементов pn. Отсюда pk = pn и k = n. ÿ
Теорема 2. Любой неприводимый над полем Fp многочлен f степени n делит многочлен (4).
Доказательство. Утверждение теоремы справедливо при n = 1. Действительно, любой многочлен первой степени ax + b имеет в поле Fp корень x = - ba -1, который по теореме Ферма является корнем многочлена xp - x и по теореме Безу последний многочлен делится на многочлен ax + b.
Пусть теперь n >1. Пусть f – неприводимый над Fp многочлен и q - его корень, Fp (q) – простое алгебраическое расширение, полученное присоединением к полю Fp корня q. Поле Fp (q) содержит элементов pn, а его мультипликативная группа состоит из pn -1 элементов. Поэтому q – корень многочлена
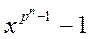 (5)
(5)
Так как многочлен f – неприводимый над Fp и имеет общий корень с многочленом (5), то многочлен (5) делится на f. Следовательно, многочлен (4) делится на f. ÿ
Теорема 3. Пусть f неприводимый над полем Fp многочлен степени n. Многочлен f делит многочлен
 (6)
(6)
тогда и только тогда, когда n делит m.
Доказательство. Утверждение теоремы справедливо при n = 1. Действительно, любой многочлен первой степени ax + b Î Fp [ x ] делит многочлен xp - x, а последний многочлен делит многочлен (6), при этом 1 делит m.
Поэтому будем предполагать, что n >1.
Необходимость. Пусть неприводимый над полем Fp многочлен f степени n делит многочлен (6), и H - поле разложения H многочлена (6), q - его корень многочлена f. Тогда
Fp Í Fp (q) Í H.
По теореме 1, поле H – конечное расширение поля Fp степени m, [ H: Fp ] = m. По теореме о строении простого алгебраического расширения поле Fp (q) - конечное расширение поля Fp степени n, [ Fp (q): Fp ] = m. По теореме о степенях расширений
m = [ H: Fp ] = [ H: Fp (q)]×[ Fp (q): Fp ] = [ H: Fp (q)]× n.
Из этого равенства следует, что n делит m.
Достаточность. Пусть n делит m, т.е. m = nk, где k Î N. Тогда имеем
m 1 = pm -1 = pnk -1 = (pn) k -1 k = (pn -1)((pn) k - 1 + (pn) k – 2 + …+ 1 k) = n 1 k 1, где k 1 Î N.
Тогда
 и многочлен (6) делится на многочлен
и многочлен (6) делится на многочлен
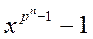
Так как по теореме 2 последний многочлен делится на многочлен f, то многочлен (6) делится на f. ÿ
Теорема 4. Число нормированных неприводимый над полем Fp многочленов степени n равно
 . (7)
. (7)
Доказательство. Рассмотрим многочлен
 (8)
(8)
Число различных корней многочлена (8) в его поле разложения равно pn. Каждый корень многочлена (8) является корнем некоторого неприводимого над Fp многочлена f степени m. При этом каждый такой многочлен f имеет m различных корней и по теореме 3 m делит n. Далее каждый неприводимый многочлен f степени m, где m делит n, является делителем многочлена (8) и все его корни являются корнями многочлена (8). Отсюда
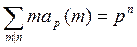 . (9)
. (9)
Применяя к этому равенству формулу обращения Мебиуса получим формулу (7).
Пример 4. 
5. С одной стороны имеем 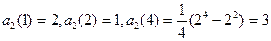 и по формуле (9)
и по формуле (9)
24 = 1× a 2(1) + 2× a 2(2) + 4× a 2(4) = 1× 2 + 2×1 + 4×3. С другой стороны, многочлен

делится на неприводимй над F 2 многочлен 2-й степени x 2 + x +1 и неприводимые над F 2 многочлены 4-й степени x 4 + x +1 и x 4 + x 3+1. Тогда
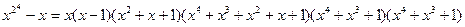 .
.
Теорема 5. Для любого простого числа p и для любого натурального числа n существует хотя бы один нормированных неприводимый над полем Fp многочлен степени n равно
. Доказательство. Для n =1 равенство (7) дает
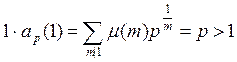 ,
,
поэтому утверждение теоремы верно.
Докажем теорему при n >1. Пусть 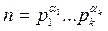 - каноническое разложение числа n, тогда все делители m числа n имеют вид:
- каноническое разложение числа n, тогда все делители m числа n имеют вид:
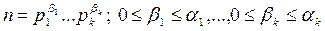 .
.
Тогда выводим

Из этой формулы находим, что  .ÿ
.ÿ



 (4)
(4)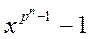 (5)
(5) (6)
(6) и многочлен (6) делится на многочлен
и многочлен (6) делится на многочлен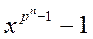
 . (7)
. (7) (8)
(8)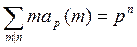 . (9)
. (9)
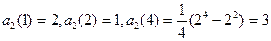 и по формуле (9)
и по формуле (9)
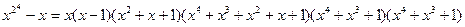 .
.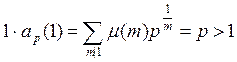 ,
,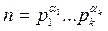 - каноническое разложение числа n, тогда все делители m числа n имеют вид:
- каноническое разложение числа n, тогда все делители m числа n имеют вид: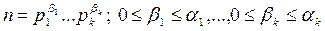 .
.
 .ÿ
.ÿ


