

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
Топ:
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования...
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Интересное:
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Определение 1. Число g называется первообразным корнем по модулю m, если порядок числа g по модулю m равен j(m), т.е. Pm (a) = j(m).
Из этого определения свойств порядка вытекают следующие свойства первообразного корня.
10 Если g первообразный корень по модулю m, то  , то aºb(mod j(m).
, то aºb(mod j(m).
20 Если g первообразный корень по модулю m, то все степени
 (1)
(1)
попарно несравнимы по модулю m.
30 Если g первообразный корень по модулю m, то любое число класса ` g по модулю m первообразный корень по модулю m.
Из 20 следует, что числа (1) образуют приведенную систему классов вычетов по модулю m, а множество всех соответствующих классов вычетов совпадает с группой Z m ´. Таким образом, для модуля m существует первообразный корень тогда и только тогда, когда группа примитивных классов Z m ´ по модулю m является циклической. При этом класс ` g является образующим элементом группы Z m ´.
Теорема 1. Для любого простого числа p существует ровно j(p -1) классов первообразных корней по модулю p.
Доказательство. Рассмотрим полную систему вычетов по модулю p:
1, 2,…, p -1. (2)
Каждое из чисел a этого множества имеет показатель d = Pp (a), который является делителем числа j(p) = p -1. Обозначим через y(d) число чисел данного множества (2), которые имеют показатель d. Тогда справедливо равенство
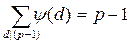 . (3)
. (3)
Из свойств функции Эйлера следует, что справедливо равенство
 . (4)
. (4)
Докажем, что y(d) £ j(d).
Если y(d) =0, то это неравенство очевидно. что
Пусть y(d) > 0. Тогда существует такое число a из множества (2), что Pp (a) = d. По свойству показателя классы
|
|
` a, ` a 2,…, ` ak (5)
образуют различные решения сравнения
xd º 1(mod p). (6)
Так как последнее сравнение имеет не более d решений, то классы (5) есть все решения последнего сравнения.
С другой стороны, любое число b из множества (2), для которого показатель равен d, удовлетворяет сравнению, т.е. класс ` b совпадает с одни из классов (5): ` b =` ak для некоторого значения k = 1, 2,…, d. Если НОД(d, k) = s > 1, то

и показатель числа a будет меньше d. Следовательно, если число b =` ak имеет показатель d, то (d, k) = 1, и таких чисел во множестве 1, 2,…, d не более j(d).
Из (3) и (4) следует
 .
.
Так как для любого d |(p -1) имеем y(d) £ j(d), то получим, что для любого d |(p -1) равенство y(d) = j(d). Последнее верно и для d = p -1. Так как y(p -1) равно числу первообразных корней во множестве (2), то теорема доказана.ÿ
Первообразный корень по модулю p можно находить, перебирая a все числа начиная с 2. Вычислить показатель Pp (a) числа a по модулю p. Если Pp (a) = p -1, то a - первообразный корень, если Pp (a) < p -1, то берем следующее число a + 1.
Алгоритм нахождения первообразного корня по модулю p.
Ввод: Простое число p.
g:= 1;
if p >2 then
Repeaet
g:= g +1; P:= function Показатель ( g, p);
until P = p -1;
Вывод: g.
Теорема 2. Пусть g – первообразный корень по модулю простого числа p > 2. Существует такое целое число t с условием, что число u, определяемое равенством
 , (7)
, (7)
не делится на p. Тогда число g + pt является первообразным корнем по любому модулю p a.
Доказательство. Действительно, имеем
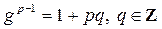 ,
,
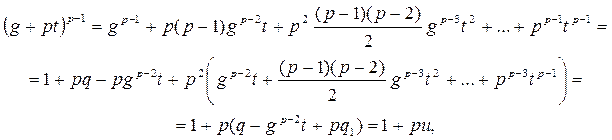 (8)
(8)
где число u вместе с числом t пробегают полную систему вычетов по модулю p. Поэтому можно указать такое t, что в равенстве (7) число u не делится на p.
При таком t имеем
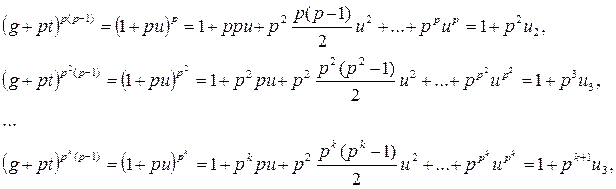 (9)
(9)
где все числа u 2, …, uk не делятся на p.
Покажем, что для любого числа a>1 число g + pt является первообразным корнем по модулю p a. Допустим, что показатель числа g + pt по модулю p aравен d. Тогда 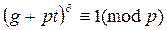 . Отсюда
. Отсюда 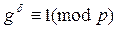 . Так как показатель числа g по модулю p равен p -1, то по свойству показателя (p -1)|d и d = (p -1) q, где q Î Z. По свойству показателя по модулю p a имеем d|j(p a), т.е. (p -1) q | (p a-1(p -1)). Отсюда q | p a-1 и q = pr, 0 £ r £ a-1.
. Так как показатель числа g по модулю p равен p -1, то по свойству показателя (p -1)|d и d = (p -1) q, где q Î Z. По свойству показателя по модулю p a имеем d|j(p a), т.е. (p -1) q | (p a-1(p -1)). Отсюда q | p a-1 и q = pr, 0 £ r £ a-1.
|
|
Равенства (8) и (9) показывают, что сравнение
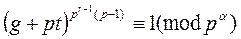
верно при r = a и неверно при r < a. Таким образом, g + pt - первообразный корнь по модулю p a. ÿ
Теорема 3. Если a ³1, g – первообразный корень по модулю p a, то нечетное из чисел g, g + p a является первообразным корнем по любому модулю 2 p a.
Теорема 4. Первообразные корни по модулю m существуют лишь в случаях, когда m = 2, 4, p a, 2 p a , где p – нечетное простое число, a - целое число ³1.
Если известно каноническое разложение числа j(m), то для нахождения первообразного корня по модулю можно воспользоваться следующим критерием первообразного корня.
Теорема 5. Пусть 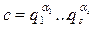 - каноническое разложение числа c = j(m), (g, m) =1. Для того, чтобы число g было первообразным корнем по модулю m необходимо и достаточно, чтобы не выполнялось ни одно из сравнений
- каноническое разложение числа c = j(m), (g, m) =1. Для того, чтобы число g было первообразным корнем по модулю m необходимо и достаточно, чтобы не выполнялось ни одно из сравнений
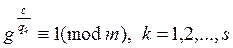 . (10)
. (10)
Доказательство. Если g - первообразный корень по модулю m, то число g имеет порядок с по модулю m и ни одно из сравнений (10) выполнятся недолжно.
Обратно, пусть не выполняется ни одно из сравнений (10). Покажем, что порядок числа g по модулю m равен c. Допустим, что Pm (g) = d < c. Тогда число  , и пусть q один из простых делителей этого числа,
, и пусть q один из простых делителей этого числа,  , u Î N. Тогда
, u Î N. Тогда
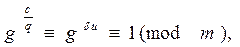
получаем противоречие с (10).ÿ
Пример 2. Найти первообразный корень по модулю 722.
Имеем 722 = 2×192. Найдем первообразный корень по модулю 19.
Находим j(19) = 18 = 22×3. Возьмем число 2.
Имеем
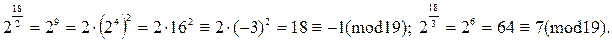
Тогда по теореме 5 2 первообразный корень по модулю 19.
Далее
 .
.
Так как 3 не делится на 19, то по теореме 2 является первообразным корнем по любой степени числа 19, т.е. 2 первообразный корень по модулю 192.
Так как число 2 + 192 = 363 нечетное, то по теореме 3 первообразным корнем по модулю 722 =2×192 является число 363.
|
|
|

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!