440305
ПАМ
Толстиков А.В.
Лекция 5. Порядки. Первообразные корни. Индексы. Характеры
1. Порядок числа и класса вычетов по модулю и их свойства..
2. Первообразные корни их существование и свойства.
3. Индексы и их свойства. Определение дискретного логарифма.
4. Квадратичные сравнения. Квадратичные вычеты. Символ Лежандра и его свойства. Символ Якоби.
5. Числовые характеры.
Литература. Виноградов И.М. – С. 396-442.
Молдовян Н.А., Молдовян А.А.. – С. 79-92.
Repeaet
g:= g +1; P:= function Показатель ( g, p);
until P = p -1;
Вывод: g.
Теорема 2. Пусть g – первообразный корень по модулю простого числа p > 2. Существует такое целое число t с условием, что число u, определяемое равенством
 , (7)
, (7)
не делится на p. Тогда число g + pt является первообразным корнем по любому модулю p a.
Доказательство. Действительно, имеем
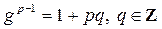 ,
,
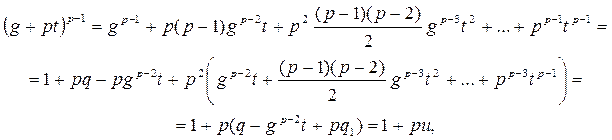 (8)
(8)
где число u вместе с числом t пробегают полную систему вычетов по модулю p. Поэтому можно указать такое t, что в равенстве (7) число u не делится на p.
При таком t имеем
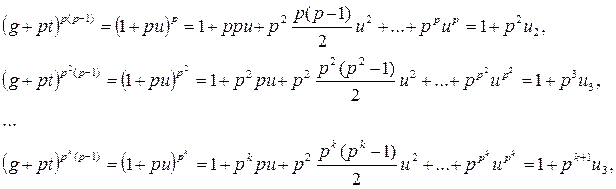 (9)
(9)
где все числа u 2, …, uk не делятся на p.
Покажем, что для любого числа a>1 число g + pt является первообразным корнем по модулю p a. Допустим, что показатель числа g + pt по модулю p aравен d. Тогда 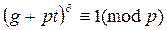 . Отсюда
. Отсюда 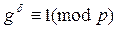 . Так как показатель числа g по модулю p равен p -1, то по свойству показателя (p -1)|d и d = (p -1) q, где q Î Z. По свойству показателя по модулю p a имеем d|j(p a), т.е. (p -1) q | (p a-1(p -1)). Отсюда q | p a-1 и q = pr, 0 £ r £ a-1.
. Так как показатель числа g по модулю p равен p -1, то по свойству показателя (p -1)|d и d = (p -1) q, где q Î Z. По свойству показателя по модулю p a имеем d|j(p a), т.е. (p -1) q | (p a-1(p -1)). Отсюда q | p a-1 и q = pr, 0 £ r £ a-1.
Равенства (8) и (9) показывают, что сравнение
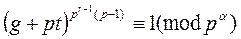
верно при r = a и неверно при r < a. Таким образом, g + pt - первообразный корнь по модулю p a. ÿ
Теорема 3. Если a ³1, g – первообразный корень по модулю p a, то нечетное из чисел g, g + p a является первообразным корнем по любому модулю 2 p a.
Теорема 4. Первообразные корни по модулю m существуют лишь в случаях, когда m = 2, 4, p a, 2 p a , где p – нечетное простое число, a - целое число ³1.
Если известно каноническое разложение числа j(m), то для нахождения первообразного корня по модулю можно воспользоваться следующим критерием первообразного корня.
Теорема 5. Пусть 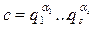 - каноническое разложение числа c = j(m), (g, m) =1. Для того, чтобы число g было первообразным корнем по модулю m необходимо и достаточно, чтобы не выполнялось ни одно из сравнений
- каноническое разложение числа c = j(m), (g, m) =1. Для того, чтобы число g было первообразным корнем по модулю m необходимо и достаточно, чтобы не выполнялось ни одно из сравнений
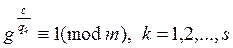 . (10)
. (10)
Доказательство. Если g - первообразный корень по модулю m, то число g имеет порядок с по модулю m и ни одно из сравнений (10) выполнятся недолжно.
Обратно, пусть не выполняется ни одно из сравнений (10). Покажем, что порядок числа g по модулю m равен c. Допустим, что Pm (g) = d < c. Тогда число  , и пусть q один из простых делителей этого числа,
, и пусть q один из простых делителей этого числа,  , u Î N. Тогда
, u Î N. Тогда
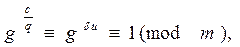
получаем противоречие с (10).ÿ
Пример 2. Найти первообразный корень по модулю 722.
Имеем 722 = 2×192. Найдем первообразный корень по модулю 19.
Находим j(19) = 18 = 22×3. Возьмем число 2.
Имеем
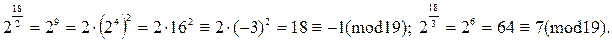
Тогда по теореме 5 2 первообразный корень по модулю 19.
Далее
 .
.
Так как 3 не делится на 19, то по теореме 2 является первообразным корнем по любой степени числа 19, т.е. 2 первообразный корень по модулю 192.
Так как число 2 + 192 = 363 нечетное, то по теореме 3 первообразным корнем по модулю 722 =2×192 является число 363.
Числовые характеры.
Определение 1. Пусть 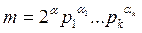 - каноническое разложение числа m, Числа c, c 0, c 1,…, ck определяются из условий:
- каноническое разложение числа m, Числа c, c 0, c 1,…, ck определяются из условий:
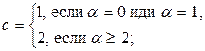
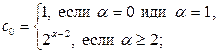 (1)
(1)
 .
.
Числа R, R 0, R 1,…, Rk обозначают какие-нибудь корни уравнений:
 (2)
(2)
т.е. числа вида  .
.
При (a, m) =1 полагаем
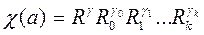 , (3)
, (3)
где g, g0, g1,…, g k - система индексов числа a, определенная соотношениями:
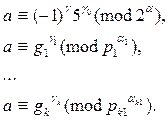 (4)
(4)
При (a, m) >1 полагаем
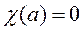 (5)
(5)
Определенную таким образом функцию  называем числовым характером по модулю m.
называем числовым характером по модулю m.
Определение 2. Если все корни R, R 0, R 1,…, Rk равны 1, то характер 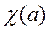 называется главным характером по модулю m. Главный характер имеет значение 1, если (a, m) =1, и значение 0, если (a, m) >1.
называется главным характером по модулю m. Главный характер имеет значение 1, если (a, m) =1, и значение 0, если (a, m) >1.
Определение 3. Два характера по модулю m считаются различными, если по крайней мере для одного значения a их значения не совпадают.
Характеры по модулю обладают следующими свойствами:
10 c(1) = 1.
20 c(ab) = c(a)c(b).
30 Если a º b (mod m), то c(a) = c(b).
40 Число различных характеров по mod m равно j(m).
50 
60 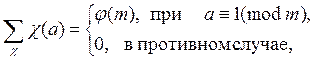
где сумма распространяется на все различные характеры c по модулю m.
70 Если c(a), c(b) характеры по модулю m, c(a)c(b) - характер по модулю m.
80 Если c0(a) - характер по модулю m, c(a) пробегает все характеры по модулю m, то c0(a)c(a) пробегает все характеры по модулю m.
90 При (l, m) =1 имеем
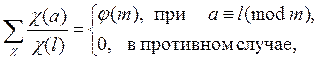
где сумма распространяется на все различные характеры c по модулю m.
Имеет место теорема.
Теорема 1. Характером по модулю m является всякая функция y(m), определенная на на всех целых числах a и удовлетворяющая усдловиям:
1) y(a) = 0, если (a, m) >1,
2) y(a) не равна тождественно нулю,
3) y(ab) = y(a)y(b),
4) Если a º b (mod m), то y(a) = y(b).
Пример 1. Построить один неглавный характер по модулю 30 и найти все его значения на полной системе вычетов 0, 1, …, 29.
Имеем 30 = 2×3×5. Вычисляем числа с, с 0, с 1, с 2 по формулам (1):
с = 1, с 0 = 1, с 1 =2, с 2 = 4.
Составим систему уравнений (2):
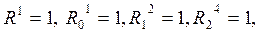
и находим ее решения
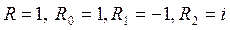 .
.
Найдем первообразные корни g 1 = 2, g 2 = 2 соответственно по модулям p 1 = 3, p 2 = 5. Рассматриваем системы сравнений (4):
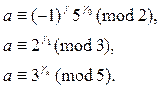 (6)
(6)
и находим по каждому числу a = 0, 1, …, 29, взаимно простому с 30 систему индексов g, g0, g1, g2 . Учитываем, что при (a, m) >1  =0.
=0.
Тогда c(0)= c(2)= c(3)= c(4)= c(5)= c(6)= c(8)= c(9)= c(10)= c(12)= c(14)= =c(15)= c(16)= c(18)= c(20)= c(21)= c(22)= c(24)= c(25)= c(26)= c(27)= c(28)=0.
Находим c(1) =1. Далее вычисляем c(a), при a = 7, 11, 13, 17, 19, 23, 29. При этих значениях a системы сравнений (6) принимают вид:

Находим решения соответствующих систем:
(g, g0, g1, g2) = (0, 0, 2, 3), (0, 0, 1, 0), (0, 0, 0, 1), (0, 0, 1, 3), (0, 0, 0, 2), (0, 0, 1, 1), (0, 0, 1, 2),
Вычисляем соответствующие значения характеров по формуле (3), которая в нашем случае принимает вид:
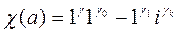 .
.
c(7) = - i, c(11) = -1, c(13) = i, c(17) = i, c(19) = -1, c(23) = - i, c(29) = 1.
Заполняем таблицу значений найденного характера:
| a
| 0
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
|
| 0
| 0
| 1
| 0
| 0
| 0
| 0
| 0
| i
| 0
| 0
|
| 1
| 0
| -1
| 0
| i
| 0
| 0
| 0
| i
| 0
| 0
|
| 2
| 0
| 0
| 0
| -i
| 0
| 0
| 0
| 0
| 0
| 1
|
азрешимо ли сравнение 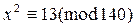 и в случае его разрешимости найти его число разрешений.
и в случае его разрешимости найти его число разрешений.
сли все корни R, R 0, R 1,…, Rk равны 1, то характер  называется главным характером по модулю m. Главный характер имеет значение 1, если (a, m) =1, и значение 0, если (, m) >1.
называется главным характером по модулю m. Главный характер имеет значение 1, если (a, m) =1, и значение 0, если (, m) >1.
пределяются из условий:
Теорема 4. Для любого простого числа p взаимно простого c числом a выполняется сравнение
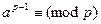 .
.
Определение 4. Пусть (G, ×) - конечная группа, a, b - элементы группы, r = ord b. Натуральное число l называется дискретным логарифмом элемента a при основанию b, если
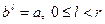 .
.
Дискретным логарифмом элемента a при основанию b обозначается символом ind ba, и называется так же индексом элемента a при основанию b.
Важную роль в вопросах применения конечных полей играют алгоритмы вычисления дискретного алгоритма.
Теорема 5. Пусть t и r - натуральные числа, r 2 ³ t. Для любого l можно указать такие целые числа x и y, что
l º xr + y (mod t); 0£ x < r, 0£ y < r.
Доказательство. Мы предположим, что 0£ l < t.. Полагаем 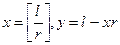 . Имеем
. Имеем 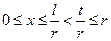 . С другой стороны,
. С другой стороны, 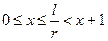 . Поэтому
. Поэтому 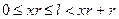 или
или 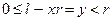 .
.
Лемма 1. Чтобы вычислить mn, где m - элемент некоторого кольца, n - натуральное число достаточно выполнить не более  умножений.
умножений.
Доказательство. Пусть 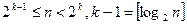 . Тогда записывая в двоичной системе счисления, получим
. Тогда записывая в двоичной системе счисления, получим
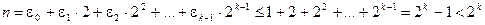 ,
,
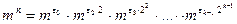 .
.
Отсюда получаем, для того, чтобы вычислить mn, можно сначала вычислить степени 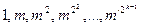 . При этом достаточно выполнить k -1 умножений (возведений в квадрат). Затем некоторые из них можно перемножить. Их не более k -1. Итак, для вычисления степени mn потребуется не более
. При этом достаточно выполнить k -1 умножений (возведений в квадрат). Затем некоторые из них можно перемножить. Их не более k -1. Итак, для вычисления степени mn потребуется не более 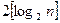 умножений.
умножений.
Теорема 6 (Гельфонда). Пусть (G, ×) - конечная группа, a, b - элементы группы, r = ord b,
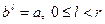 . (3)
. (3)
Тогда число l можно найти, выполнив не более  операций умножения на элементы группы G.
операций умножения на элементы группы G.
Доказательство. Полагаем 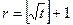 . Рассмотрим ряды
. Рассмотрим ряды
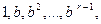 (4)
(4)
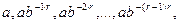 (5)
(5)
Если 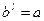 разрешимо относительно l, то по теореме 5 представим l в виде
разрешимо относительно l, то по теореме 5 представим l в виде
l º xr + y (mod t); 0£ x < r, 0£ y < r.
Так как r = ord b, то 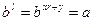 в том и только в том случае, когда
в том и только в том случае, когда
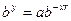 , (6)
, (6)
т.е. когда найдется элемент ряда (4), который совпадает с каким-нибудь членом ряда (5).
Подсчитаем число операций, позволяющих установить равенство (6). При вычислении элементов ряда (5) потребуется выполнить не более r -2 умножений. При вычислении  в силу леммы 1 требуется выполнить не белее чем
в силу леммы 1 требуется выполнить не белее чем 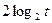 умножений. И не более чем r -1 умножений потребуется для вычисления всех членов ряда (5). Поэтому число операций для решения уравнения (3) не превосходит
умножений. И не более чем r -1 умножений потребуется для вычисления всех членов ряда (5). Поэтому число операций для решения уравнения (3) не превосходит 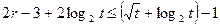 .
.
1. Криптография. Метод шифрования "с открытым ключем".
Шифрование - это кодирование данных с целью защиты от несанкционированного доступа. Процесс кодирования называется шифрованием, а процесс декодирования называется расшифровыванием. Само кодированное сообщение называется шифрованным, а применяемый метод кодирования называется шифром.
Основное требование к шифру состоит в том, чтобы расшифровка, была возможна только при наличии санкции, т.е. некоторой дополнительной информации, называемой ключом шифра. Процесс декодирования шифрованной информации без ключа называется дешифрованием (или раскрытием шифра)..
Область знаний о шифрах, методах их создания и раскрытия называется криптографией или тайнописью.
На практике тот шифр считается надежным, если раскрытие шифра стоит в денежном выражении больше, чем сама шифрованная информация. С другой стороны надежным считается такой шифр, если на его раскрытие уйдет такое время, за которое информация, содержащаяся в шифрованном сообщении устареет и не будет иметь практически ни какой ценности.
Наиболее часто используются шифры с симметричным ключом, при которых ключи шифрования и расшифровывания совпадают.
Например, шифры - подстановки (т.е. замена отдельных символов сообщения другими, по определенному правилу). Например, каждому символу сообщения сопоставляется по определенному правилу ругой символ.

Слово a шифруется по правилу b= S (a), а расшифровывается по правилу a= S -1 (b). Здесь ключ шифрования и расшифровывания один и тот же.
Преимущество.
1) Простота шифрования.
2) Высокая скорость шифрования.
Недостатки:
1) трудности с надежной передачи секретного ключа (ключ передается с помощью более надежных, но медленных шифров).
2) невысокая криптостойкость ключа, особенно, если злоумышленнику известна часть сообщения передаваемого этим ключем.
Для повышения криптостойкости применяется предварительное перемешивание битов сообщения по определенному правилу.
Электронная подпись.
1.
440305
ПАМ
Толстиков А.В.
Лекция 5. Порядки. Первообразные корни. Индексы. Характеры
1. Порядок числа и класса вычетов по модулю и их свойства..
2. Первообразные корни их существование и свойства.
3. Индексы и их свойства. Определение дискретного логарифма.
4. Квадратичные сравнения. Квадратичные вычеты. Символ Лежандра и его свойства. Символ Якоби.
5. Числовые характеры.
Литература. Виноградов И.М. – С. 396-442.
Молдовян Н.А., Молдовян А.А.. – С. 79-92.



 , (7)
, (7)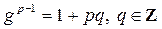 ,
,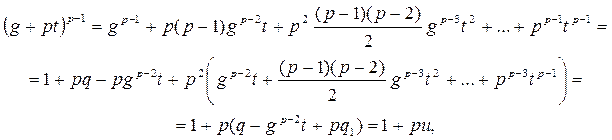 (8)
(8)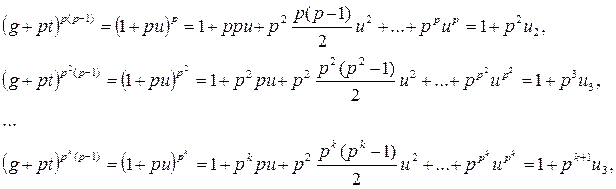 (9)
(9)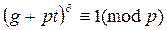 . Отсюда
. Отсюда 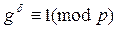 . Так как показатель числа g по модулю p равен p -1, то по свойству показателя (p -1)|d и d = (p -1) q, где q Î Z. По свойству показателя по модулю p a имеем d|j(p a), т.е. (p -1) q | (p a-1(p -1)). Отсюда q | p a-1 и q = pr, 0 £ r £ a-1.
. Так как показатель числа g по модулю p равен p -1, то по свойству показателя (p -1)|d и d = (p -1) q, где q Î Z. По свойству показателя по модулю p a имеем d|j(p a), т.е. (p -1) q | (p a-1(p -1)). Отсюда q | p a-1 и q = pr, 0 £ r £ a-1.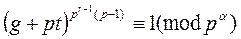
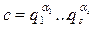 - каноническое разложение числа c = j(m), (g, m) =1. Для того, чтобы число g было первообразным корнем по модулю m необходимо и достаточно, чтобы не выполнялось ни одно из сравнений
- каноническое разложение числа c = j(m), (g, m) =1. Для того, чтобы число g было первообразным корнем по модулю m необходимо и достаточно, чтобы не выполнялось ни одно из сравнений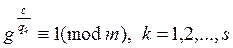 . (10)
. (10) , и пусть q один из простых делителей этого числа,
, и пусть q один из простых делителей этого числа,  , u Î N. Тогда
, u Î N. Тогда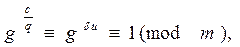
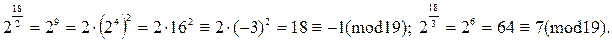
 .
.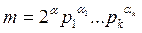 - каноническое разложение числа m, Числа c, c 0, c 1,…, ck определяются из условий:
- каноническое разложение числа m, Числа c, c 0, c 1,…, ck определяются из условий: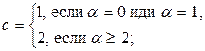
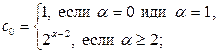 (1)
(1) .
. (2)
(2) .
.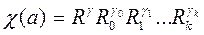 , (3)
, (3)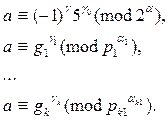 (4)
(4)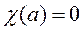 (5)
(5)  называем числовым характером по модулю m.
называем числовым характером по модулю m.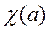 называется главным характером по модулю m. Главный характер имеет значение 1, если (a, m) =1, и значение 0, если (a, m) >1.
называется главным характером по модулю m. Главный характер имеет значение 1, если (a, m) =1, и значение 0, если (a, m) >1.
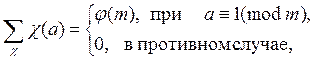
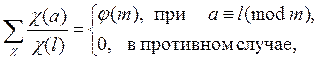
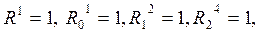
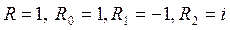 .
.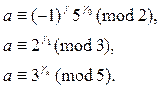 (6)
(6)
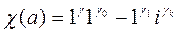 .
.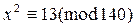 и в случае его разрешимости найти его число разрешений.
и в случае его разрешимости найти его число разрешений.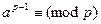 .
. 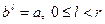 .
.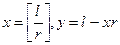 . Имеем
. Имеем 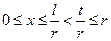 . С другой стороны,
. С другой стороны, 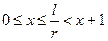 . Поэтому
. Поэтому 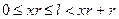 или
или 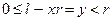 .
.  умножений.
умножений.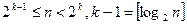 . Тогда записывая в двоичной системе счисления, получим
. Тогда записывая в двоичной системе счисления, получим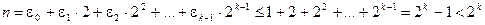 ,
,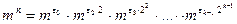 .
.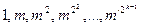 . При этом достаточно выполнить k -1 умножений (возведений в квадрат). Затем некоторые из них можно перемножить. Их не более k -1. Итак, для вычисления степени mn потребуется не более
. При этом достаточно выполнить k -1 умножений (возведений в квадрат). Затем некоторые из них можно перемножить. Их не более k -1. Итак, для вычисления степени mn потребуется не более 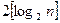 умножений.
умножений.  операций умножения на элементы группы G.
операций умножения на элементы группы G.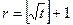 . Рассмотрим ряды
. Рассмотрим ряды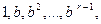 (4)
(4)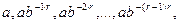 (5)
(5)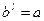 разрешимо относительно l, то по теореме 5 представим l в виде
разрешимо относительно l, то по теореме 5 представим l в виде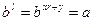 в том и только в том случае, когда
в том и только в том случае, когда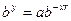 , (6)
, (6) в силу леммы 1 требуется выполнить не белее чем
в силу леммы 1 требуется выполнить не белее чем 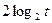 умножений. И не более чем r -1 умножений потребуется для вычисления всех членов ряда (5). Поэтому число операций для решения уравнения (3) не превосходит
умножений. И не более чем r -1 умножений потребуется для вычисления всех членов ряда (5). Поэтому число операций для решения уравнения (3) не превосходит 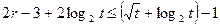 .
. 



