Определение 1. Целое число a > 1 называется составным, если его можно представить в виде произведения двух целых чисел, больших единицы, т.е.
a = a 1 a 2, (1)
где a 1 > 1, a 2 > 1, a 1 , a 2 Î Z.
Определение 2. Целое число p > 1 называется простым, если его нельзя представить в виде произведения двух целых чисел, больших единицы, т.е. нельзя представить в виде:
p = a 1 a 2, (2)
где a 1 > 1, a 2 > 1, a 1 , a 2 Î Z.
Теорема 1. Любое целое число a > 1 имеет хотя бы один простой делитель.
Доказательство. Рассмотрим множество M всех делителей числа a, которые больше 1. Множество M не пусто, так как a | a и a > 1. Следовательно, во множестве M есть наименьшее число. Обозначим это число через p и покажем, что p есть простое число. Допустим противное, что число p составное. Тогда его можно представить в виде (2), где a 1 > 1, a 2 > 1, a 1 , a 2 Î Z. Отсюда a 1| p. Так как p | a, то a 1| a и a 1 = p / a 2 < p. Получили противоречие. Следовательно, p есть простое число.ÿ
Теорема 2. Целое число a > 1 составное тогда и только тогда, когда оно имеет хотя бы один простой делитель p  .
.
Доказательство. Пусть число a > 1 составное. Тогда для него имеет место представление (1). Покажем, что хотя бы одно из чисел a 1 или a 2  . Допустим противное. Тогда оба числа a 1 и a 2
. Допустим противное. Тогда оба числа a 1 и a 2 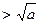 . Отсюда
. Отсюда
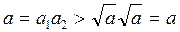 .
.
Получаем противоречие. Таким образом, хотя бы одно из чисел a 1 или a 2 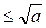 . Допустим для определенности, что a 1
. Допустим для определенности, что a 1  . Так как число a 1 > 1, то оно имеет простой делитель p, который является делителем числа a. Так как
. Так как число a 1 > 1, то оно имеет простой делитель p, который является делителем числа a. Так как 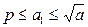 , то первая часть теоремы доказана.
, то первая часть теоремы доказана.
Обратно, если число a > 1 имеет простой делитель p 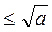 , то
, то 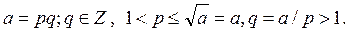 Следовательно, число a составное.ÿ
Следовательно, число a составное.ÿ
Теорема 3. Целое число p > 1 простое тогда и только тогда, когда оно не имеет простых делителей p  .
.
Доказательство. Доказательство основывается на теореме 2 ипроводится методом от противного. ÿ
Из теорем 1 и 2 следует метод проверки целого числа на простоту.
Алгоритм проверки числа на простоту.
Ввод: число a.
r:=1 ;d:= 2;
while r ¹ 0 and d 2 £ a do (q, r): = div (a, d); d:= d + 1; end while
if r =0 then s:= «число составное» else s:= «число простое»; end if.
Вывод: s и x (t), y (t).
На теоремах 2 и 3 основан метод нахождения всех простых чисел в заданных пределах, называемый решетом Эротосфена. Например, чтобы найти все простые числа в пределах от 1 до n поступают следующим образом:
1. Выписывают все числа от 1 до n. Первое число этой последовательности 1 непростое и его вычеркиваем.
2. Первое не вычеркнутое число 2, оно простое. Вычеркиваем каждое второе число, считая с 3, т.е. вычеркиваем все числа кратные 2, кроме 2.
3. Первое не вычеркнутое число 3, оно простое. Вычеркиваем в ряде каждое третье число, считая с 4, вычеркнутые числа учитываются, т.е. вычеркиваем все числа кратные 3, кроме 3.
4. Первое не вычеркнутое число 5, оно простое, если бы оно было непростое, то имело простой делитель p 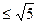 и было вычеркнуто на предыдущих шагах. Вычеркиваем в ряде каждое пятое число, считая с 6, вычеркнутые числа учитываются, т.е. вычеркиваем все числа кратные 5, кроме 5.
и было вычеркнуто на предыдущих шагах. Вычеркиваем в ряде каждое пятое число, считая с 6, вычеркнутые числа учитываются, т.е. вычеркиваем все числа кратные 5, кроме 5.
Продолжаем этот процесс до тех пор пока на некотором шаге не появится первое невычеркнутое число a 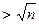 . Тогда это число a и все невычеркнутые в ряду числа будут простыми, так как они не имеют простых делителей p
. Тогда это число a и все невычеркнутые в ряду числа будут простыми, так как они не имеют простых делителей p 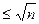 .
.
Пример 1. Найти все простые числа от 1 до 50.
 На промежутке от 1 до 50 содержится 15 чисел.
На промежутке от 1 до 50 содержится 15 чисел.
Алгоритм «решето Эротосфена».
Ввод: Число n.
m:=0; r:= b; a 1:= a;; b 1:= b;
{Занесение единиц в массив}
for i:=2… n; ai: = 1; end for;
p:=2; m:=2;
while p 2 £ n do m:= p 2;
{Вычеркивание чисел кратных p }
while m £ n do ai: = 0; m:= m + p;; end while;
m:= p + 1;
{Нахождение очередного невычеркнутого числа}
while am = 0 do m:= m + 1; end while;
p:= m
end while;
{Занесение полученных простых чисел в массив P }
т:= 0; for i:=2… n; if ai: = 1 then m:= m +1; Pm: = i; end if; end for.
Вывод: m и P.
Теорема 4 (Евклида). Простых чисел бесконечно много.
Доказательство. Доказываем методом от противного. Допустим, что простых чисел конечное число и p 1, p 2, …, pn – список всех простых чисел. Составим натуральное число a = p 1 p 2· …· pn +1. Так как число a > 1, по теореме 1 оно имеет хотя бы один простой делитель p, который совпадает с одним из данных простых чисел. Тогда p | a и p |(p 1 p 2· …· pn). По свойствам делимости получаем p |1 и по свойствам делимости p = ±1. Получаем противоречие с определением простого числа.ÿ
Вопрос, о том как простые числа распределены в натуральном ряду стоял в течении более 2000 тысяч лет и впервые существенные результаты в этом направлении были получены во второй половине 19 века русским математиком П.Л. Чебышевым.
Пусть 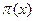 - число всех простых чисел, не превосходящих x. Функция
- число всех простых чисел, не превосходящих x. Функция 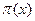 называется функцией распределения простых чисел. В силу примера 1 получаем
называется функцией распределения простых чисел. В силу примера 1 получаем
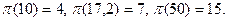 График функции
График функции  выглядит следующим образом.
выглядит следующим образом.
 Теорема 5 (неравенства Чебышева). Существуют такие два действительных числа a и b, 0 < a <1< b,что выполняется неравенства
Теорема 5 (неравенства Чебышева). Существуют такие два действительных числа a и b, 0 < a <1< b,что выполняется неравенства
 .
.
П.Л.Чебышев показал, что 0,921 £ a <1< b £ 1,106.
Теорема 5 (Теорема Чебышева, 1848 г.). Если существует предел
 , (3)
, (3)
то он равен (3) существует доказал.
То что предел (3) существует доказали независимо друг от друга Адамар и Валле-Пуссен в 1896 году. Из этого следует, что
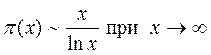 .
.
В 20 веке было получено много интересных результатов, связанных с поведением функции  .
.
Основная теорема арифметики
Теорема 1 (основная теорема арифметики). Любое целое число a > 1 представляется в виде произведения простых чисел:
a = p 1 p 2… pk, (1)
где p 1, p 2,…, pk – простые числа и такое представление единственно с точностью до порядка следования простых сомножителей, т.е. если есть второе представление вида
a = q 1 q 2… qm, (2)
где q 1, q 2,…, qm – простые числа, то k = m и при соответствующей перестановке сомножителей pi = qi для всех i = 1, 2,…, k.
Доказательство. Существования. Докажем методом математической индукции по a. Если a = 2, то разложение (1) имеет место при k =1, p 1 = 2. Допустим, что разложение (1) имеет место для любых целых чисел b, 2 £ b < a. И докажем справедливость утверждения теоремы для числа a.
Если a - простое число, то формула (1) имеет место при k =1, p 1 = a. Если a - составное число, то
a = bc, где 2 £ b, c < a; b, c Î Z. (3)
По индуктивному предположению каждое из чисел b, c представляется в виде произведения простых чисел
b =p 1 p 2… pl, c =pl+ 1 p l+ 2… pk.
Подставляя b, c в формулу (3) получим требуемое разложение.
Единственность. Доказательство единственности опирается на следующие леммы:
Лемма 1. Если p – простое число, a –любое целое число, то либо p | a либо (p, a) = 1.
Доказательство. Пусть D = НОД(p, a). Тогда D | p. Так как p – простое число, то либо D = 1, либо D = p. В первом случае числа p, a взаимно простые, (p, a) = 1. Во втором случае, по определению НОД p | a. ÿ
Лемма 2. Если p – простое число, a, b – любые целые числа и p | ab, то p | a или p | b.
Доказательство. Пусть p | ab. Тогда по лемме 1 либо p | a либо (p, a) = 1. В первом случае утверждение леммы справедливо, а во втором случае, по свойству взаимно простых чисел получаем p | b. ÿ
Лемма 3. Если p, q 1, q 2,…, qm – простые числа, и p |(q 1 q 2… qm), то p совпадает хотя бы с одним из простых сомножителей q 1, q 2,…, qm.
Доказательство. Докажем утверждение методом математической индукции по m. Пусть m = 1. Тогда p | q 1. По определению делимости q 1 = pa. Так как q 1простое число, то a = 1 или p =1. Последнее невозможно. Поэтому a =1 и q 1 = p.
Предположим, что утверждение теоремы справедливо для m = k и докажем его для m = k + 1 сомножителей. Пусть p |(q 1 q 2… qk qk +1). По лемме 2 p |(q 1 q 2… qk) или p | qk +1. В первом случае по индуктивному предположению p совпадает хотя бы с одним из сомножителей. q 1,…, qk. Во втором случае по доказанному выше p = qk +1. ÿ
Продолжение доказательства теоремы. Доказываем теорему методом от противного. Допустим, что единственность не имеет места. И пусть a наименьшее натуральное число для которого единственность разложения не имеет места. Тогда для числа a имеют место два разложения (1) и (2). Тогда
a = p 1 p 2… pk = q 1 q 2… qm. (4)
Левая часть этого равенства делится на простое число p 1, поэтому и правая часть его делится на p 1. Тогда по лемме 3, число p 1 совпадает хотя бы с одним из сомножителей. q 1,…, qm. Можно считать, что p 1 = q 1, в противном случае можно переставить сомножители во втором произведении. Так как p 1| a, то a = p 1 b, где b Î N, b < a. Тогда из равенства (4) получаем:
b = p 2… pk = q 2… qm.
Так как b Î N, b < a, то для числа b имеет место единственность разложения, т.е. k = m и при соответствующей перестановке сомножителей pi = qi для всех i = 2, 2,…, k. Последнее противоречит тому, что разложения (1) и (2) числа a различны. ÿ
Рассмотрим разложение (1) числа a на простые множители. В этом разложении могут оказаться одинаковые простые множители. Произведение всех простых множителей запишем в виде натуральной степени одного простого числа и представим число a в виде:
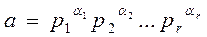 , (5)
, (5)
где 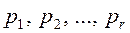 - попарно различные простые числа, a1, a2,…,a r - натуральные числа (иногда в этом разложении допускаются и нулевые показатели, когда соответствующий неприводимый многочлен).
- попарно различные простые числа, a1, a2,…,a r - натуральные числа (иногда в этом разложении допускаются и нулевые показатели, когда соответствующий неприводимый многочлен).
Представление целого числа в виде (5) называется каноническим представление целого числа a. В силу теоремы предыдущего параграфа получаем следующую теорему.
Теорема 2. Для любых целого числа a > 1 каноническое разложение (6) существует и оно однозначно с точностью до порядка следования степеней простых чисел.
Теорема 3. Пусть 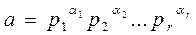 ,
,  - канонические разложения целых чисел a, b (допускаются нулевые показатели). Тогда справедливы следующие утверждения:
- канонические разложения целых чисел a, b (допускаются нулевые показатели). Тогда справедливы следующие утверждения:
1) a, делит b.тогда и только тогда. когда a i £ b i для любого i = 1, 2, …, r;
2) 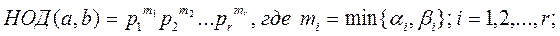
3) 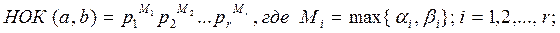
Доказательство. 1. Пусть a, делит b. Тогда по определению делимости a = bc, где c Î Z. Пусть теперь 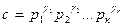 - каноническое разложение числа с. Тогда предыдущее равенство представится в виде
- каноническое разложение числа с. Тогда предыдущее равенство представится в виде
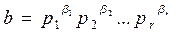
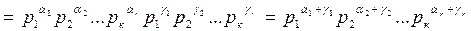 .
.
В силу единственности канонического разложения получаем равенства b i = a i + g i для любого i = 1, 2, …, r. Так как g i ³ 0, то отсюда получаем требуемое неравенство b i ³ a i.
Обратно, если b i ³ a i для любого i = 1, 2, …, r, то и тогда получаем b i = a i + g i, где g i ³ 0. Тогда
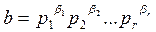
 ,
,
где с Î Z.
2. Пусть  . Так как mi = min{a i, b i } £ a i, b i для любого i = 1, 2, …, r, то по доказанному свойству 1 D \ f, D | g.
. Так как mi = min{a i, b i } £ a i, b i для любого i = 1, 2, …, r, то по доказанному свойству 1 D \ f, D | g.
Пусть теперь 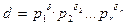 - общий делитель чисел a и b. Тогда по свойству 1 d i £ a i, d i £ b i для любого i = 1, 2, …, r, то d i £min{a i, b i } = mi. Тогда по свойству 1 имеем d \ D. По определению многочлен есть НОД многочленов f и g.
- общий делитель чисел a и b. Тогда по свойству 1 d i £ a i, d i £ b i для любого i = 1, 2, …, r, то d i £min{a i, b i } = mi. Тогда по свойству 1 имеем d \ D. По определению многочлен есть НОД многочленов f и g.
Аналогичным образом доказывается третья часть теоремы 2.
В теории чисел более двух тысяч лет решались две основные задачи:
1. Задача тестирования целого числа на простоту: найти наиболее быстрый алгоритм определения, является данное целое число a простым или составным.
2. Задача факторизации: нужно разложить число a на множители, если известно, что оно простое.
Оказалось, что эти задачи принципиально отличаются по трудности. Распознать, на простоту наугад взятое число, содержащее 125 и более десятичных знаков можно за несколько минут, а для того чтобы разложить такое число на множители может потребоваться миллионы лет машинного времени.
В связи с появлением в криптографии алгоритмов несимметричного шифрования оказалось, что эти задачи имеют большое практическое значение. Через две тысячи лет теория чисел стала прикладной наукой. В последние два десятилетия интерес к этим задачам теории чисел многократно возрос. Появилось большое число работ, посвященных этим задачам.
Отметим, что задача факторизации более трудная задача чем задача тестирования числа на простоту, на чем и основан алгоритм RSA. В последние десятилетия появилось множество различных алгоритмов тестирования и факторизации целых чисел. Найдены быстрые алгоритмы тестирования на простоту целых чисел и новые алгоритмы факторизации, но тем не менее скорость факторизации чисел на десятки порядков ниже скорости их тестирования.
В начале 80-х годов Адлеман, Померанс и Румели предложили детерминированный алгоритм проверки простоты чисел, для заданного натурального числа n алгоритм делает  операций. Существенное улучшение их алгоритма в 1981 году получено Х.Ленстрой. Реализация этого алгоритма позволила проверять на простоту числа n порядка 10100 за несколько минут. В настоящее время удается тестировать на простоту числа порядка 101000. В 1992 г Адлеман и Хуанг предложили вероятностный алгоритм проверки на простоту чисел, полиномиальной сложности, теоретическая оценка
операций. Существенное улучшение их алгоритма в 1981 году получено Х.Ленстрой. Реализация этого алгоритма позволила проверять на простоту числа n порядка 10100 за несколько минут. В настоящее время удается тестировать на простоту числа порядка 101000. В 1992 г Адлеман и Хуанг предложили вероятностный алгоритм проверки на простоту чисел, полиномиальной сложности, теоретическая оценка 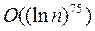 операций. Индийскими математиками Агравала, Кайала и Саксены в 2002 г. получен алгоритм проверки целого числа на простоту полиномиальной сложности, теоретическая оценка
операций. Индийскими математиками Агравала, Кайала и Саксены в 2002 г. получен алгоритм проверки целого числа на простоту полиномиальной сложности, теоретическая оценка 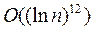 операций.
операций.
Алгоритм факторизации числа n с помощью пробного деления, опирающийся на теорему 2 предыдущей главы требует 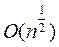 арифметических операций. Алгоритм Шермана - Лемена, полученный в 1974 году, требует
арифметических операций. Алгоритм Шермана - Лемена, полученный в 1974 году, требует 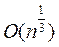 арифметических операций. Лучший из детерминированных алгоритмов факторизации Полларда - Штрассена, найденный в 1974 году, требует
арифметических операций. Лучший из детерминированных алгоритмов факторизации Полларда - Штрассена, найденный в 1974 году, требует 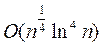 арифметических операций для разложение числа на два множителя.
арифметических операций для разложение числа на два множителя.
Пусть
 .
.
Существуют алгоритмы факторизации натуральных чисел n, делающие 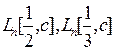 арифметических операций. Например, алгоритм квадратичного решета составляет
арифметических операций. Например, алгоритм квадратичного решета составляет 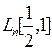 арифметических операций и позволил факторизовать 129-значное RSA-число. Другой алгоритм решета числового поля позволил разложить в 2000 году 155-значное RSA - число – число 512 бит. На факторизацию последнего числа ушло 8400 mips-year (при миллионе операций в секунду 8400 годов).
арифметических операций и позволил факторизовать 129-значное RSA-число. Другой алгоритм решета числового поля позволил разложить в 2000 году 155-значное RSA - число – число 512 бит. На факторизацию последнего числа ушло 8400 mips-year (при миллионе операций в секунду 8400 годов).



 .
. . Допустим противное. Тогда оба числа a 1 и a 2
. Допустим противное. Тогда оба числа a 1 и a 2 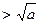 . Отсюда
. Отсюда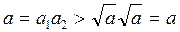 .
.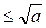 . Допустим для определенности, что a 1
. Допустим для определенности, что a 1 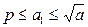 , то первая часть теоремы доказана.
, то первая часть теоремы доказана.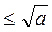 , то
, то 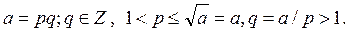 Следовательно, число a составное.ÿ
Следовательно, число a составное.ÿ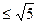 и было вычеркнуто на предыдущих шагах. Вычеркиваем в ряде каждое пятое число, считая с 6, вычеркнутые числа учитываются, т.е. вычеркиваем все числа кратные 5, кроме 5.
и было вычеркнуто на предыдущих шагах. Вычеркиваем в ряде каждое пятое число, считая с 6, вычеркнутые числа учитываются, т.е. вычеркиваем все числа кратные 5, кроме 5.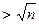 . Тогда это число a и все невычеркнутые в ряду числа будут простыми, так как они не имеют простых делителей p
. Тогда это число a и все невычеркнутые в ряду числа будут простыми, так как они не имеют простых делителей p 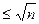 .
. На промежутке от 1 до 50 содержится 15 чисел.
На промежутке от 1 до 50 содержится 15 чисел.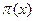 - число всех простых чисел, не превосходящих x. Функция
- число всех простых чисел, не превосходящих x. Функция 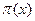 называется функцией распределения простых чисел. В силу примера 1 получаем
называется функцией распределения простых чисел. В силу примера 1 получаем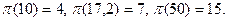 График функции
График функции  выглядит следующим образом.
выглядит следующим образом. Теорема 5 (неравенства Чебышева). Существуют такие два действительных числа a и b, 0 < a <1< b,что выполняется неравенства
Теорема 5 (неравенства Чебышева). Существуют такие два действительных числа a и b, 0 < a <1< b,что выполняется неравенства .
. , (3)
, (3)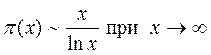 .
.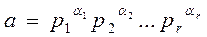 , (5)
, (5) - попарно различные простые числа, a1, a2,…,a r - натуральные числа (иногда в этом разложении допускаются и нулевые показатели, когда соответствующий неприводимый многочлен).
- попарно различные простые числа, a1, a2,…,a r - натуральные числа (иногда в этом разложении допускаются и нулевые показатели, когда соответствующий неприводимый многочлен).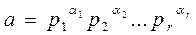 ,
,  - канонические разложения целых чисел a, b (допускаются нулевые показатели). Тогда справедливы следующие утверждения:
- канонические разложения целых чисел a, b (допускаются нулевые показатели). Тогда справедливы следующие утверждения: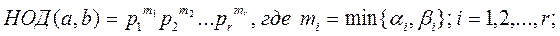
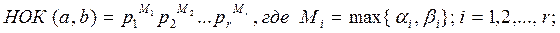
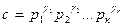 - каноническое разложение числа с. Тогда предыдущее равенство представится в виде
- каноническое разложение числа с. Тогда предыдущее равенство представится в виде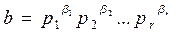
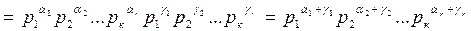 .
.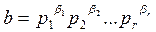
 ,
, . Так как mi = min{a i, b i } £ a i, b i для любого i = 1, 2, …, r, то по доказанному свойству 1 D \ f, D | g.
. Так как mi = min{a i, b i } £ a i, b i для любого i = 1, 2, …, r, то по доказанному свойству 1 D \ f, D | g.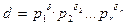 - общий делитель чисел a и b. Тогда по свойству 1 d i £ a i, d i £ b i для любого i = 1, 2, …, r, то d i £min{a i, b i } = mi. Тогда по свойству 1 имеем d \ D. По определению многочлен есть НОД многочленов f и g.
- общий делитель чисел a и b. Тогда по свойству 1 d i £ a i, d i £ b i для любого i = 1, 2, …, r, то d i £min{a i, b i } = mi. Тогда по свойству 1 имеем d \ D. По определению многочлен есть НОД многочленов f и g. операций. Существенное улучшение их алгоритма в 1981 году получено Х.Ленстрой. Реализация этого алгоритма позволила проверять на простоту числа n порядка 10100 за несколько минут. В настоящее время удается тестировать на простоту числа порядка 101000. В 1992 г Адлеман и Хуанг предложили вероятностный алгоритм проверки на простоту чисел, полиномиальной сложности, теоретическая оценка
операций. Существенное улучшение их алгоритма в 1981 году получено Х.Ленстрой. Реализация этого алгоритма позволила проверять на простоту числа n порядка 10100 за несколько минут. В настоящее время удается тестировать на простоту числа порядка 101000. В 1992 г Адлеман и Хуанг предложили вероятностный алгоритм проверки на простоту чисел, полиномиальной сложности, теоретическая оценка 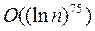 операций. Индийскими математиками Агравала, Кайала и Саксены в 2002 г. получен алгоритм проверки целого числа на простоту полиномиальной сложности, теоретическая оценка
операций. Индийскими математиками Агравала, Кайала и Саксены в 2002 г. получен алгоритм проверки целого числа на простоту полиномиальной сложности, теоретическая оценка 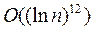 операций.
операций.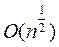 арифметических операций. Алгоритм Шермана - Лемена, полученный в 1974 году, требует
арифметических операций. Алгоритм Шермана - Лемена, полученный в 1974 году, требует 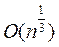 арифметических операций. Лучший из детерминированных алгоритмов факторизации Полларда - Штрассена, найденный в 1974 году, требует
арифметических операций. Лучший из детерминированных алгоритмов факторизации Полларда - Штрассена, найденный в 1974 году, требует 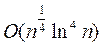 арифметических операций для разложение числа на два множителя.
арифметических операций для разложение числа на два множителя. .
.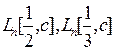 арифметических операций. Например, алгоритм квадратичного решета составляет
арифметических операций. Например, алгоритм квадратичного решета составляет 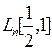 арифметических операций и позволил факторизовать 129-значное RSA-число. Другой алгоритм решета числового поля позволил разложить в 2000 году 155-значное RSA - число – число 512 бит. На факторизацию последнего числа ушло 8400 mips-year (при миллионе операций в секунду 8400 годов).
арифметических операций и позволил факторизовать 129-значное RSA-число. Другой алгоритм решета числового поля позволил разложить в 2000 году 155-значное RSA - число – число 512 бит. На факторизацию последнего числа ушло 8400 mips-year (при миллионе операций в секунду 8400 годов).