

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...
Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Интересное:
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
ПАМ
Толстиков А.В.
Лекция 3. Теория делимости целых чисел.
1. Делимость целых чисел. Теорема о делении с остатком.
2. Представление целого числа в g-ичной системе счисления.
3. Целочисленная арифметика многократной точности.
4. Наибольший общий делитель целых чисел и наименьшее общее кратное целых чисел. Алгоритм Евклида.
5. Цепные дроби и их свойства. Линейные диофантовы уравнения и их системы.
6. Простые и составные числа. Критерий простоты числа. Теорема Евклида. Неравенства Чебышева.
7. Основная теорема арифметики и следствия из нее.
Литература. Виноградов И.М. – С. 7-54;
Василенко О.Н. –С. 254- 273;
Коробейников А. Г. и др. –С. 2-17
Делимость целых чисел. Теорема о делении с остатком.
Определение 1. Говорят, что целое число a делит целое число b, если существует такое целое число с, что b = a с. При этом число a называется делителем числа b, число – с – частным, число b называют также кратным числу a. Обозначаем a | b.
Теорема 1. Для любых целых чисел a, b, с, d, e, f справедливы свойства:
10. a| a;
20. a |0;
30. 1| a;
40. a | b и b | c Þ a | c;
50. a | b и a | c Þ a |(b + c);
60. a | b и a | c Þ a |(b - c);
70. a | b и a |(b + c)Þ a | c;
80. a | b и c | d Þ ac |(bd);
90. a | b и a | c Þ a |(db + ec);
100. a | b и b | a Þ a = ± b;
110. a | b и b ¹ 0, Þ | a | £| b |;
120. a | b и | b | <| a |, Þ b = 0.
Доказательство. Докажем свойство 4, а остальные свойства предоставляем доказать самостоятельно. Пусть a | b и b | c. Тогда по определению делимости
b = a с и c = bd,
где с, d Î Z. Отсюда c = a (dc), где dc Î Z. Тогда по определению 1 a | c. ÿ
Теорема 2 (теорема о делении с остатком). Для любых целых чисел a, где b ¹ 0, существует такая единственная пара целых чисел q и r, что
b = aq + r, 0£ r < | b |. (1)
|
|
Доказательство. Существование. Рассмотрим множество
M = { x = a - by | y Î Z, x ³ 0} Ì Z.
Множество M не пусто; если a ³ 0, то число a = a - b ·0Î M; если a < 0, то число x = a - | b | a Î M. Тогда множество M содержит минимальный элемент r,, а соответствующее ему число y обозначим через q. Тогда
r = a – bq, a= bq + r, q и r Î Z, r ³ 0.
Покажем, что r < | b |. Допустим, что r ³ | b |. Отсюда
r - | b | ³ 0, r - | b | = a – b (q ±1) Î Z,
и число r - | b |< r Î M. Получаем противоречие. Следовательно, числа q и r удовлетворяющие условиям теоремы 2 существуют.
Единственность. Допустим, что существует еще одна пара целых q и r чисел, удовлетворяющих условиям теоремы. Тогда имеем
b = aq + r, 0£ r < | b |;
b = aq 1+ r 1, 0£ r 1 < | b |.
Вычитая эти равенства и неравенства почленно, получаем
A (q - q 1)+ (r - r 1) = 0, -| b | < r - r 1 < | b |. (2)
Из равенства (2) по свойствам делимости следует, что b | (r - r 1). Так как | r - r 1| < | b |,
то по свойству 11 делимости получаем r - r 1 = 0, r = r 1. Тогда из равенства (2) находим A (q - q 1) = 0, q - q 1 = 0, q = q 1. Полученное противоречие доказывает единственность деления с остатком. ÿ
Замечания 1. Число r в равенстве (1) теоремы 2 называется остатком, число q неполным частным.
2. По теореме 2 любое целое число a представляется в одном и только одном виде: b = aq + 0, b = aq + 1 ,…, b = aq + (a -1);
End for
if c 0:= 1 then
for i = 1… n; (f, ci): = div (ai - bi + f, g); end for
else if c 0:= -1 then
for i = 1… n; (f, ci): = div (bi - ai + f, g); end for
end if;
Выход: 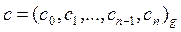 .
.
При вычитании двух n -значных чисел требуется выполнить n операций деления с остатком и 2 n операций вычитаний чисел величиной с цифру и n сравнений.
Пусть даны два целых числа
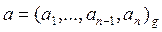 ,
, 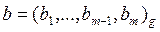
Перенос в другой разряд обозначаем через f (флаг переноса). Находим произведение чисел 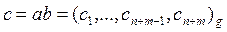 . Произведение чисел можно выполнять по формулам:
. Произведение чисел можно выполнять по формулам:
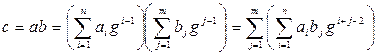 , (1)
, (1)
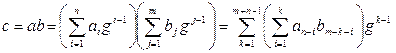 , (2)
, (2)
где при l <1 мы полагаем al = 0, bl = 0.
Алгоритм, реализуемый по формуле (1) напоминает «умножение столбиком», а по формуле (2) «умножение быстрым столбиком»
Алгоритм умножения неотрицательных целых чисел столбиком.
|
|
Вход: 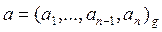 ,
, 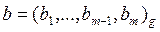 ;
;
c = 0; f:=0;
for j = 1… m;
if bi > 0 then
for i = 1… n; (f, ci + j- 1): = div (ci + j- 1 + ai bj + f, g); end for
end if;
End for
Выход: 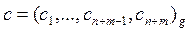 .
.
При умножении n -значного числа на m -значное число по этому алгоритму требуется выполнить не более nm операций умножения, nm операций деления с остатком, 2 nm операций сложения.
Алгоритм умножения неотрицательных целых чисел быстрый столбик.
Вход: 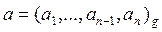 ,
, 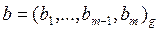 ;
;
c = 0; f:=0;
for k = 1… n+m- 1;
for i = 1… k;
if n-i >0 and m-k + i > 0 then f:= f+ an-i · bm-k+i end if;
end for
(f, ck): = div (f, g);
End for
Выход: 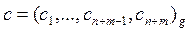 .
.
При умножении n -значного числа на m -значное число требуется выполнить nm операций умножения, n + m операций сложения и n + m операций деления с остатком.
В 1962 году студент МГУ, ныне профессор А.А.Карацуба предложил более быстрый способ умножения больших многозначных чисел. Предположим, что у нас имеется два 2 n -значных числа:
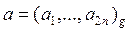 ,
, 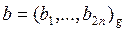 .
.
Положим
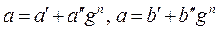 ,
,
где
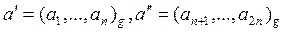 ,
, 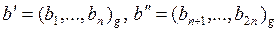 .
.
Тогда
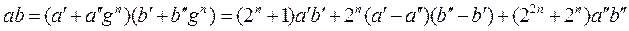 . (3)
. (3)
Таким образом, при умножении двух 2 n -значных чисел по формуле (3) нужно 3 умножения n -значных чисел, 4 сложения и 2 вычитания и 4 сдвига n-значных чисел. По формуле требуется 4 сложения и 3 сдвига. (4) требуется 4 умножения и 3 сдвига.
При больших n метод Карацубы становится более эффективным, чем «быстрый столбец».Если обозначить через T (n) число битовых операций для умножения двух n -разрядных чисел, то
T (2 n) = 3 T (n) + cn, (4)
где c – константа. Используя эти соображения получим, что
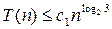 .
.
Установлено, что существует метод умножения двух n -значных двоичных чисел, требующий не более O(n ·ln n · lnln n) двоичных операций.
Пусть дано целое число
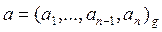
иодноразрядное число b, 1£ b < g. Находим частное 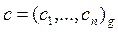 и остаток r.
и остаток r.
Алгоритм деления неотрицательного целого числа на однозначное число.
Вход: 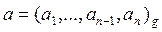 ,
, 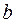 ;
;
r = 0;
for i = 1… n;
(ci, r): = div (rg+ai, b);
End for
Выход: 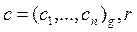 .
.
Рассмотрим алгоритм деления целых чисел в общем случае. Задача деления целых чисел упирается в задачу подбора очередной цифры неполного частного в следующей ситуации. Пусть 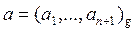 ,
, 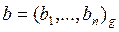 , причем bn >0, a / b < g. Нам нужно найти частное от деления a на b:
, причем bn >0, a / b < g. Нам нужно найти частное от деления a на b:
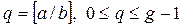 . (5)
. (5)
Условие a / b < g равносильно неравенству a / g < b, что равносильно неравенству
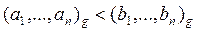 (6)
(6)
Обозначим
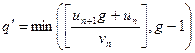 (7)
(7)
Лемма 1. При указанных выше условиях справедливо неравенство
|
|
q £ q `. (8)
При дополнительном условии bn > [ g /2] справедливо неравенство
q `-2 £ q. (9)
Замечание. Чтобы оказаться в рамках второго условия леммы 1 необходимо нормализовать числа a и b, умножив их оба на 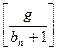 . При этом доказывается, что частное q не изменяется.
. При этом доказывается, что частное q не изменяется.
Алгоритм деления неотрицательных целых чисел.
Вход: делимое 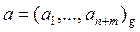 , делитель
, делитель 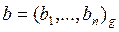 , n ³ 2;
, n ³ 2;
Нормализация чисел a и b (нахождение нормализирующего множителя и умножение на него чисел a и b).
(d, k): = div (g, bn +1);
t:=0; for i = 1… n + m; (t, ai): = div (tg + dai, g); end for;
if t >0 then m:= m+ 1; am:= t; end if;
t:=0; for i = 1… n; (t, bi): = div (tg + dbi, g); end for;
for j = m …1;
Подбор очередной цифры qm неполного частного. Обеспечение условий подбора очередной цифры (a / b < g, a < gb, e = gb)
e:= (0, b 1,…, bn);
p:=1;
for v = 0 … g -1;
for i = n …1;
if bi > an+i then p:=1; break else if bi < an+i then break; end if;
end for
if p =1 then break;end if;
end for
Нахождение приближенного значения q ` цифры qm неполного частного по формуле (7).
if bn = an+j then q`:= g - 1 else (q`, t): = div (an+j g + an+j- 1, bn); end if;
Уточнение приближенного значения q ` цифры qm неполного частного.
while bn- 1 q` > ( an+j g + an+j- 1 - bnq` ) g + an+j- 2 do q`:= q`- 1; end while;
Проверка правильности подбора приближенного значения q ` цифры qm и ее уточнение:
t:=0; for i = 1… n; (t, aj+i): = div (aj+i - q`bi + tg, g); end for;
qm := q`;
if t <0 then qm := qm -1; t:=0;
for i = 1… n; (t, aj+i): = div (bi-aj+i + tg, g); end for;
end if;
qm := qm + vg; (не всегда цифра в g -ичной системе счисления.
end for;
Нахождение правильного представления неполного частного и остатка.
t:=0; for i = 1… n; (t, qi): = div (qj + tg, g); end for;
if t >0 then n:= n+ 1; qm:= t; end if;
t = 0; for i = 1… n; (ri, t): = div (tg+ai, d); end for
Выход: неполное частное 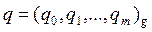 , остаток
, остаток 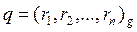 .
.
Возведение в натуральную степень. Предполагается, что операция умножения многозначных чисел уже реализована. Требуется число a возвести в степень числа m. Представим число m в двоичной системе счисления:
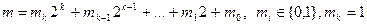 . (6)
. (6)
Тогда возможны два возможных алгоритма вычисления степени am , которые получаются из следующих равенств:
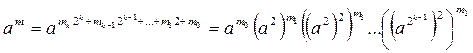 , (7)
, (7)
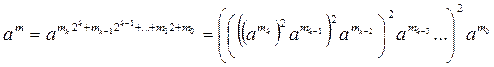 . (8)
. (8)
Алгоритмы называются бинарными алгоритмами возведения в степень.
|
|
В первом случае находятся степени 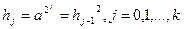 . Затем находится произведение всех hj,, для которых mi ¹0:
. Затем находится произведение всех hj,, для которых mi ¹0:
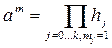 .
.
Во втором случае находят 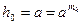 , далее
, далее
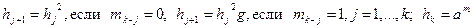 .
.
Первый алгоритм возведения в степень.
Вход: основание a, показатель степени m;
b:=1; h:= a;
while m > 0 do (m, r): = div (m, 2);
if r >0 then b:= bh; end if;
if m > 0 then h:= h·h; end if;
end while;
Выход: b.
Второй алгоритм возведения в степень.
Вход: основание a, показатель степени m;
b:= a; h:=2 j:=-1;
while m > 0 do j:= j +1; (m, mj): = div (m, 2); end while;
for i = j-1…0; if mj >0 then b:= b·b·a else b:= b·b; end if; end for;
Выход: b.
Первый способ более экономен в отношении памяти, во втором способе происходит экономия на умножении.
Основная теорема арифметики
Теорема 1 (основная теорема арифметики). Любое целое число a > 1 представляется в виде произведения простых чисел:
a = p 1 p 2… pk, (1)
где p 1, p 2,…, pk – простые числа и такое представление единственно с точностью до порядка следования простых сомножителей, т.е. если есть второе представление вида
a = q 1 q 2… qm, (2)
где q 1, q 2,…, qm – простые числа, то k = m и при соответствующей перестановке сомножителей pi = qi для всех i = 1, 2,…, k.
Доказательство. Существования. Докажем методом математической индукции по a. Если a = 2, то разложение (1) имеет место при k =1, p 1 = 2. Допустим, что разложение (1) имеет место для любых целых чисел b, 2 £ b < a. И докажем справедливость утверждения теоремы для числа a.
Если a - простое число, то формула (1) имеет место при k =1, p 1 = a. Если a - составное число, то
a = bc, где 2 £ b, c < a; b, c Î Z. (3)
По индуктивному предположению каждое из чисел b, c представляется в виде произведения простых чисел
b =p 1 p 2… pl, c =pl+ 1 p l+ 2… pk.
Подставляя b, c в формулу (3) получим требуемое разложение.
Единственность. Доказательство единственности опирается на следующие леммы:
Лемма 1. Если p – простое число, a –любое целое число, то либо p | a либо (p, a) = 1.
Доказательство. Пусть D = НОД(p, a). Тогда D | p. Так как p – простое число, то либо D = 1, либо D = p. В первом случае числа p, a взаимно простые, (p, a) = 1. Во втором случае, по определению НОД p | a. ÿ
Лемма 2. Если p – простое число, a, b – любые целые числа и p | ab, то p | a или p | b.
Доказательство. Пусть p | ab. Тогда по лемме 1 либо p | a либо (p, a) = 1. В первом случае утверждение леммы справедливо, а во втором случае, по свойству взаимно простых чисел получаем p | b. ÿ
Лемма 3. Если p, q 1, q 2,…, qm – простые числа, и p |(q 1 q 2… qm), то p совпадает хотя бы с одним из простых сомножителей q 1, q 2,…, qm.
Доказательство. Докажем утверждение методом математической индукции по m. Пусть m = 1. Тогда p | q 1. По определению делимости q 1 = pa. Так как q 1простое число, то a = 1 или p =1. Последнее невозможно. Поэтому a =1 и q 1 = p.
|
|
Предположим, что утверждение теоремы справедливо для m = k и докажем его для m = k + 1 сомножителей. Пусть p |(q 1 q 2… qk qk +1). По лемме 2 p |(q 1 q 2… qk) или p | qk +1. В первом случае по индуктивному предположению p совпадает хотя бы с одним из сомножителей. q 1,…, qk. Во втором случае по доказанному выше p = qk +1. ÿ
Продолжение доказательства теоремы. Доказываем теорему методом от противного. Допустим, что единственность не имеет места. И пусть a наименьшее натуральное число для которого единственность разложения не имеет места. Тогда для числа a имеют место два разложения (1) и (2). Тогда
a = p 1 p 2… pk = q 1 q 2… qm. (4)
Левая часть этого равенства делится на простое число p 1, поэтому и правая часть его делится на p 1. Тогда по лемме 3, число p 1 совпадает хотя бы с одним из сомножителей. q 1,…, qm. Можно считать, что p 1 = q 1, в противном случае можно переставить сомножители во втором произведении. Так как p 1| a, то a = p 1 b, где b Î N, b < a. Тогда из равенства (4) получаем:
b = p 2… pk = q 2… qm.
Так как b Î N, b < a, то для числа b имеет место единственность разложения, т.е. k = m и при соответствующей перестановке сомножителей pi = qi для всех i = 2, 2,…, k. Последнее противоречит тому, что разложения (1) и (2) числа a различны. ÿ
Рассмотрим разложение (1) числа a на простые множители. В этом разложении могут оказаться одинаковые простые множители. Произведение всех простых множителей запишем в виде натуральной степени одного простого числа и представим число a в виде:
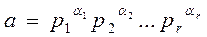 , (5)
, (5)
где 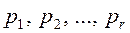 - попарно различные простые числа, a1, a2,…,a r - натуральные числа (иногда в этом разложении допускаются и нулевые показатели, когда соответствующий неприводимый многочлен).
- попарно различные простые числа, a1, a2,…,a r - натуральные числа (иногда в этом разложении допускаются и нулевые показатели, когда соответствующий неприводимый многочлен).
Представление целого числа в виде (5) называется каноническим представление целого числа a. В силу теоремы предыдущего параграфа получаем следующую теорему.
Теорема 2. Для любых целого числа a > 1 каноническое разложение (6) существует и оно однозначно с точностью до порядка следования степеней простых чисел.
Теорема 3. Пусть 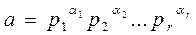 ,
,  - канонические разложения целых чисел a, b (допускаются нулевые показатели). Тогда справедливы следующие утверждения:
- канонические разложения целых чисел a, b (допускаются нулевые показатели). Тогда справедливы следующие утверждения:
1) a, делит b.тогда и только тогда. когда a i £ b i для любого i = 1, 2, …, r;
2) 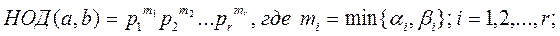
3) 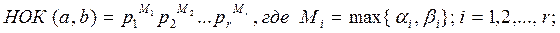
Доказательство. 1. Пусть a, делит b. Тогда по определению делимости a = bc, где c Î Z. Пусть теперь 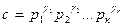 - каноническое разложение числа с. Тогда предыдущее равенство представится в виде
- каноническое разложение числа с. Тогда предыдущее равенство представится в виде
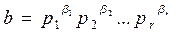
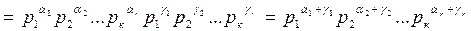 .
.
В силу единственности канонического разложения получаем равенства b i = a i + g i для любого i = 1, 2, …, r. Так как g i ³ 0, то отсюда получаем требуемое неравенство b i ³ a i.
Обратно, если b i ³ a i для любого i = 1, 2, …, r, то и тогда получаем b i = a i + g i, где g i ³ 0. Тогда
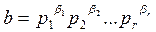
 ,
,
где с Î Z.
2. Пусть  . Так как mi = min{a i, b i } £ a i, b i для любого i = 1, 2, …, r, то по доказанному свойству 1 D \ f, D | g.
. Так как mi = min{a i, b i } £ a i, b i для любого i = 1, 2, …, r, то по доказанному свойству 1 D \ f, D | g.
Пусть теперь 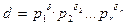 - общий делитель чисел a и b. Тогда по свойству 1 d i £ a i, d i £ b i для любого i = 1, 2, …, r, то d i £min{a i, b i } = mi. Тогда по свойству 1 имеем d \ D. По определению многочлен есть НОД многочленов f и g.
- общий делитель чисел a и b. Тогда по свойству 1 d i £ a i, d i £ b i для любого i = 1, 2, …, r, то d i £min{a i, b i } = mi. Тогда по свойству 1 имеем d \ D. По определению многочлен есть НОД многочленов f и g.
Аналогичным образом доказывается третья часть теоремы 2.
В теории чисел более двух тысяч лет решались две основные задачи:
1. Задача тестирования целого числа на простоту: найти наиболее быстрый алгоритм определения, является данное целое число a простым или составным.
2. Задача факторизации: нужно разложить число a на множители, если известно, что оно простое.
Оказалось, что эти задачи принципиально отличаются по трудности. Распознать, на простоту наугад взятое число, содержащее 125 и более десятичных знаков можно за несколько минут, а для того чтобы разложить такое число на множители может потребоваться миллионы лет машинного времени.
В связи с появлением в криптографии алгоритмов несимметричного шифрования оказалось, что эти задачи имеют большое практическое значение. Через две тысячи лет теория чисел стала прикладной наукой. В последние два десятилетия интерес к этим задачам теории чисел многократно возрос. Появилось большое число работ, посвященных этим задачам.
Отметим, что задача факторизации более трудная задача чем задача тестирования числа на простоту, на чем и основан алгоритм RSA. В последние десятилетия появилось множество различных алгоритмов тестирования и факторизации целых чисел. Найдены быстрые алгоритмы тестирования на простоту целых чисел и новые алгоритмы факторизации, но тем не менее скорость факторизации чисел на десятки порядков ниже скорости их тестирования.
В начале 80-х годов Адлеман, Померанс и Румели предложили детерминированный алгоритм проверки простоты чисел, для заданного натурального числа n алгоритм делает  операций. Существенное улучшение их алгоритма в 1981 году получено Х.Ленстрой. Реализация этого алгоритма позволила проверять на простоту числа n порядка 10100 за несколько минут. В настоящее время удается тестировать на простоту числа порядка 101000. В 1992 г Адлеман и Хуанг предложили вероятностный алгоритм проверки на простоту чисел, полиномиальной сложности, теоретическая оценка
операций. Существенное улучшение их алгоритма в 1981 году получено Х.Ленстрой. Реализация этого алгоритма позволила проверять на простоту числа n порядка 10100 за несколько минут. В настоящее время удается тестировать на простоту числа порядка 101000. В 1992 г Адлеман и Хуанг предложили вероятностный алгоритм проверки на простоту чисел, полиномиальной сложности, теоретическая оценка 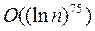 операций. Индийскими математиками Агравала, Кайала и Саксены в 2002 г. получен алгоритм проверки целого числа на простоту полиномиальной сложности, теоретическая оценка
операций. Индийскими математиками Агравала, Кайала и Саксены в 2002 г. получен алгоритм проверки целого числа на простоту полиномиальной сложности, теоретическая оценка 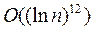 операций.
операций.
Алгоритм факторизации числа n с помощью пробного деления, опирающийся на теорему 2 предыдущей главы требует 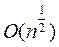 арифметических операций. Алгоритм Шермана - Лемена, полученный в 1974 году, требует
арифметических операций. Алгоритм Шермана - Лемена, полученный в 1974 году, требует 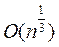 арифметических операций. Лучший из детерминированных алгоритмов факторизации Полларда - Штрассена, найденный в 1974 году, требует
арифметических операций. Лучший из детерминированных алгоритмов факторизации Полларда - Штрассена, найденный в 1974 году, требует 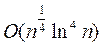 арифметических операций для разложение числа на два множителя.
арифметических операций для разложение числа на два множителя.
Пусть
 .
.
Существуют алгоритмы факторизации натуральных чисел n, делающие 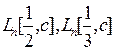 арифметических операций. Например, алгоритм квадратичного решета составляет
арифметических операций. Например, алгоритм квадратичного решета составляет 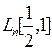 арифметических операций и позволил факторизовать 129-значное RSA-число. Другой алгоритм решета числового поля позволил разложить в 2000 году 155-значное RSA - число – число 512 бит. На факторизацию последнего числа ушло 8400 mips-year (при миллионе операций в секунду 8400 годов).
арифметических операций и позволил факторизовать 129-значное RSA-число. Другой алгоритм решета числового поля позволил разложить в 2000 году 155-значное RSA - число – число 512 бит. На факторизацию последнего числа ушло 8400 mips-year (при миллионе операций в секунду 8400 годов).
ПАМ
Толстиков А.В.
Лекция 3. Теория делимости целых чисел.
1. Делимость целых чисел. Теорема о делении с остатком.
2. Представление целого числа в g-ичной системе счисления.
3. Целочисленная арифметика многократной точности.
4. Наибольший общий делитель целых чисел и наименьшее общее кратное целых чисел. Алгоритм Евклида.
5. Цепные дроби и их свойства. Линейные диофантовы уравнения и их системы.
6. Простые и составные числа. Критерий простоты числа. Теорема Евклида. Неравенства Чебышева.
7. Основная теорема арифметики и следствия из нее.
Литература. Виноградов И.М. – С. 7-54;
Василенко О.Н. –С. 254- 273;
Коробейников А. Г. и др. –С. 2-17
|
|
|
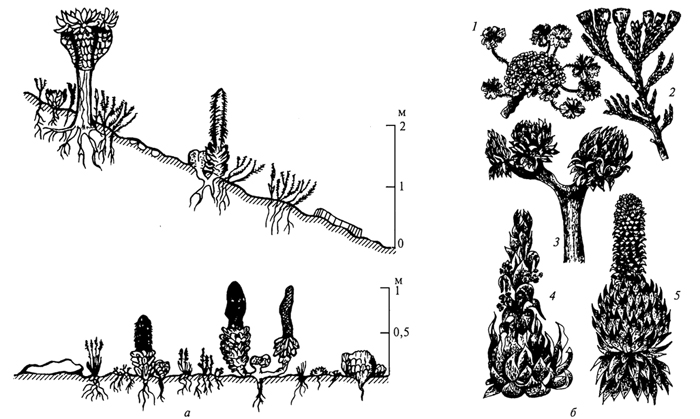
Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...
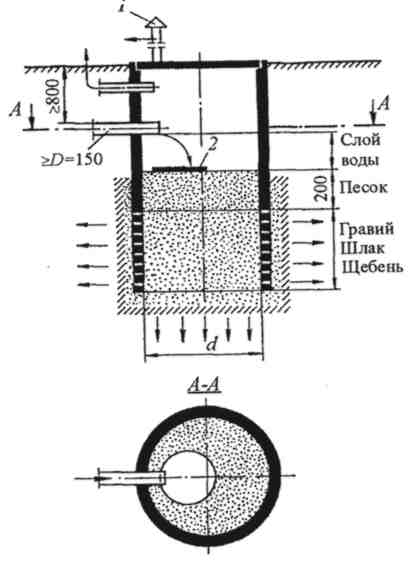
Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...
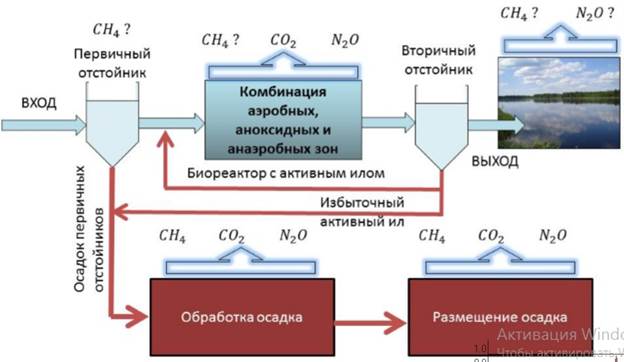
Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!