Определение 1. Пусть p – простое число; a 1, a 2,…, an Î Fp, an ¹ 0. Уравнение вида
d x+n = a 1d x+n- 1 + a 2d x+n- 2 + …+ an d x (1)
называется линейным рекуррентным уравнением над полем Fp порядка n. Многочлен
f (l) = l n - a 1l n- 1 - …+ an Î Fp [l] (2)
называется характеристическим многочленом уравнения (1). Последовательность d элементов поля Fp называется решением уравнения (1), если она удовлетворяет уравнению (1). Первые n членов последовательности d0, d1,…, d n - 1 последовательности называются начальными членами последовательности d. Они однозначно определяют всю последовательность d.
Решение линейного рекуррентного уравнения (1) называют также рекуррентной последовательностью.
Через s (f) = s F (f) обозначаем множество всех решений уравнения (1) над полем F = Fp с характеристическим многочленом f.
Пример 1. Пусть p = 2, n = 2, f = l2 - l -1. Список всех решений над полем F 2 уравнения d x + 2 = d x + 1 + d x приведен в таблице.
| x
| 0
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| …
|
| d x
| 0
| 0
| 0
| 0
| 0
| 0
| 0
| 0
| 0
| …
|
| d x
| 0
| 1
| 1
| 0
| 1
| 1
| 0
| 1
| 1
| …
|
| d x
| 1
| 0
| 1
| 1
| 0
| 1
| 1
| 0
| 1
| …
|
| d x
| 1
| 1
| 0
| 1
| 1
| 0
| 1
| 1
| 0
| …
|
Пример 2. Пусть p = 3, n = 2, f = l2 - l -1. Список всех решений над полем F 3 уравнения d x + 2 = d x + 1 + d x приведен в таблице.
| x
| 0
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| …
|
| d x
| 0
| 0
| 0
| 0
| 0
| 0
| 0
| 0
| 0
| 0
| …
|
| d x
| 0
| 1
| 1
| 2
| 0
| 2
| 2
| 1
| 0
| 1
| …
|
| d x
| 1
| 0
| 1
| 1
| 2
| 0
| 2
| 2
| 1
| 0
| …
|
| d x
| 0
| 2
| 2
| 1
| 0
| 1
| 1
| 2
| 0
| 2
| …
|
| d x
| 2
| 0
| 2
| 2
| 1
| 0
| 1
| 1
| 2
| 0
| …
|
| d x
| 1
| 1
| 2
| 0
| 2
| 2
| 1
| 0
| 1
| 1
| …
|
| d x
| 1
| 2
| 0
| 2
| 2
| 1
| 0
| 1
| 1
| 2
| …
|
| d x
| 2
| 1
| 0
| 1
| 1
| 2
| 0
| 2
| 2
| 1
| …
|
| d x
| 2
| 2
| 1
| 0
| 1
| 1
| 2
| 0
| 2
| 2
| …
|
Теорема 1. Число всех решений линейного рекуррентного уравнения порядка n над полем Fp равно pn, в том числе pn - 1 ненулевых, т.о.
| s F (f)| = pn = p deg f.
Доказательство. Число решений уравнения (1) равно числу всевозможных различных наборов начальных членов (d0, d1,…, d n - 1). Каждый такой набор есть размещение с повторениями из p элементов поля Fp. Следовательно, число решений уравнения равно pn.
Теорема 2. Пусть d = {d x }- какое-нибудь решение линейного рекуррентного уравнения (1), x, y – неотрицательные целые числа. Если
d x = d y , d x+ 1 = d y+ 1, …, d x+n- 1 = d y+n- 1, (3)
то d x + n = d y + n, если к тому же x > 0, y > 0, то d x - 1 = d y - 1.
Доказательство. Из уравнения (1) имеем
d x+n = a 1d x+n- 1 + a 2d x+n- 2 + …+ an d x, d y+n = a 1d y+n- 1 + a 2d y+n- 2 + …+ an d y.
Тогда в силу равенств (3) получаем d x + n = d y + n.
Если x > 0, y > 0, то запишем уравнения (1) при x равном x – 1 и y – 1
d x+n- 1 = a 1d x+n- 2 + a 2d x+n- 3 + …+ an d x- 1, d y+n- 1 = a 1d y+n- 2 + a 2d y+n- 3 + …+ an d y - 1.
Так как an ¹ 0, то в в силу равенств (3) получаем d x - 1 = d y - 1.
Теорема 3. Пусть S (f) - система (s (f), +, Fp). Тогда:
1) система S (f) – векторное пространство над полем Fp, замкнутое относительно сдвига;
2) для любого решения d Î s (f) и многочлена g Î Fp [l] имеем g ·d Î s (f);
3) векторное пространство S (f) изоморфно n -мерному координатному пространству Vn над полем Fp.
Доказательство. 1.Пусть 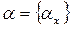 , b = {b x }Î s (f). Тогда для любого неотрицательного числа x выполняются равенства
, b = {b x }Î s (f). Тогда для любого неотрицательного числа x выполняются равенства
a x+n = a 1a x+n- 1 + a 2a x+n- 2 + …+ an a x, b x+n = a 1b x+n- 1 + a 2b x+n- 2 + …+ an b x.
Складывая эти равенства почленно, получаем равенство
a x+n + b x+n = a 1(a x+n- 1 + b x+n- 1) + a 2(a x+n- 2 + b x+n- 2) + …+ an (a x + b x),
которое показывает, что последовательность a+b = {a x + b x }Î s (f).
Умножая обе части равенства (1) на элемент c Î Fp, получаем равенство
c a x+n = a 1(c a x+n- 1) + a 2(c a x+n- 2) + …+ an (c a x),
которое показывает, что последовательность c a = { c a x }Î s (f). Так как s (f) Ì s, а множество s является векторным пространством над Fp, то из доказанного выше следует, что s (f) – векторное пространство над полем Fp.
Так как для любой последовательности aÎ s (f), последовательность T ·a Î s (f)и так как любая последовательности 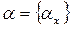 Î s (f) может быть получена сдвигом последовательности b = {b x }Î s (f), где для любого a = {a x }, T ·a = b = {b x }. имеем b x + 1 = a x, а b0 – произвольный элемент из Fp. Поэтому T · s = s.
Î s (f) может быть получена сдвигом последовательности b = {b x }Î s (f), где для любого a = {a x }, T ·a = b = {b x }. имеем b x + 1 = a x, а b0 – произвольный элемент из Fp. Поэтому T · s = s.
2. Пусть d Î s (f) и многочлена g (l) = b 0 + b 1l + …+ bk l k Î Fp [l]. Тогда
g ·d = b 0 d + b 1 T ·d + …+ bkTk · d.
По доказательству первого пункта имеем
d, T ·d,…, Tk · d, b 0 d, b 1 T ·d,…, bkTk · d, b 0 d + b 1 T ·d + …+ bkTk · d Î s (f).
Таким образом, g ·d Î s (f).
3. Зададим отображение Y: s (f) ® Vn по правилу:
Y(d) = (d0, d1,…, d n - 1).
Это отображение Y является биекцией, в силу того, что любая рекуррентная последовательность однозначно определяется характеристическим уравнением и ее начальными членами. Далее из определения суммы последовательностей и произведения последовательности на число следует, что для любых последовательностей 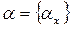 , b = {b x }Î s (f) и любого c Î Fp выполняются свойства
, b = {b x }Î s (f) и любого c Î Fp выполняются свойства
Y(a + b) = Y({a x } + {b x }) = Y({a x + b x }) = (a0 + b0, a1 + b1,…, a n - 1 + b n - 1) =
= (a0, a1,…, a n - 1 ) + (b0, b1,…, b n - 1) = Y(a) + Y(b),
Y(с a) = Y(с {a x }) = Y({ с a x }) = (с a0, с a1,…, с a n - 1 ) = с (a0, a1,…, a n - 1 ) = с Y(a).
По определению отображение Y является изоморфизмом, а векторные пространства S (f) и Vn изоморфные.
Так как dim Vn = n и S (f) @ Vn, то dim S (f)= n и базис пространства S (f) состоит из n решений.
Определение 2. Решение d линейного рекуррентного уравнения (1) называется главным решением, если набор решений (d, T ·d,…, Tn - 1· d) является базисом пространства S (f).
Пример 3. Решение r = {r x }Î s (f) уравнения (1) с начальными значениями
r0 = r1 = …= r n - 2 = 0, r n - 1 = 1
является главным, так как векторам r, T ·r,…, Tn - 1· r при отображении Y соответствуют векторы
(0, 0,…, 0, 1), (0, 0,…, 1, r n), …, (1, r n,…, r2 n -3, r2 n -2),
которые образуют базис пространства Vn. Тогда по свойству изоморфизма векторы r, T ·r,…, Tn - 1· r образуют базис пространства S (f) и решение d - главное.



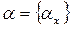 , b = {b x }Î s (f). Тогда для любого неотрицательного числа x выполняются равенства
, b = {b x }Î s (f). Тогда для любого неотрицательного числа x выполняются равенства


