Разложение определителя по элементам строки или столбца.

Операции над матрицами.

1. A и В считаются равными, если они имеют одинаковую размерность и соответствующие элементы равны.

2. Для того, чтобы сложить 2 матрицы, достаточно сложить соответствующие элементы.

3. Умножение матрицы на число: В = λA; достаточно умножить на это число все элементы.

4. Умножение матриц: для перемножения А и В надо выполнить следующие условия: длинна а строки матрицы А должна равняться высоте столбца матрицы В; число столбцов А = число строк В; АВ<>ВА; A (m*k) à m/k; B (k*n) à k/n; A*B = mk/kn = m/n; примеры

Определитель матрицы. Вычисляется только для квадратной матрицы. Определитель второго порядка Δ=detA=|a _ij | = a₁₁ a₂₂ — a₁₂ a₂₁; Определитель третьего порядка — число найденной по правилу Саррюса.(Примеры)

Минор и алгебраическое дополнение. Минор — это определитель, полученный вычеркиванием строки или столбца. Базисный минор — любой минор r порядка м-ы А отличный от 0. Минором Мij матрицы A, n*n, называется определитель, полученный вычеркиванием i строки и j столбца из матрицы А. Минор, взятый с определенным знаком называется алгебраическим дополнением элемента. A_ij = (-1) ^( i + j) M_ij

Разложение определителя по элементам строки или столбца.

Рассмотрим i-тую строку: Δ= a_i1 A_i1 + a_i2 A_i2 +…+a_in A_in

Рассмотрим j-тый столбец: Δ = a_1j A_1j + a_2j A_2j+…+a_nj A_nj

Свойства определителя n-го порядка.

1. Если все элементы строки или столбца равны нулю, то и Δ= 0;

2. При перестановке 2 строк (столбцов) знак определителя меняется на противоположный.

3. Определитель не изменится, если транспонировать соответствующую матрицу.

4. Общий множитель строки или столбца можно выносить за знак определителя.

5. Если элементы строки или столбца представляют собой сумму слагаемых, то определитель равен сумме Δей, элементами которых в данной строке или столбце являются эти слагаемые.

6. Если две строки или столбца имеют одинаковые элементы, то такой Δ= 0

7. Определитель не изменяется, если к элементам строки или столбца прибавить соответствующие элементы другой строки или столбца, умноженные на некоторое число k, где k — любое действительное число.(Примеры)

Обратная матрица. Обратная матрица к исходной матрице А называется матрица А ^-1, удовлетворяющая условию A*A ^{- 1} =A ^{- 1} A=E.

ТЕОРЕМА о существовании обратной матрицы. Для того, чтобы квадратная матрица А имела обратную матрицу, необходимо и достаточно (<=>), чтобы матрица А была невыражденной — detA<>0;

1. необходимые условия. Дано: А, А ^-1; Док-ть: detA ¹ 0; Док-во: Предположим detA=0; AA ^-1 =E; |AA ^{- 1} | = |A| |A ^-1 | = |E| = 1; |AA ^{- 1} | =0; Противоречие, значит |A| ¹ 0;

2. достаточные условия: Дано A, detA ¹ 0; Док-ть: A ^-1 -?; Док-во: AA ^-1 =E -?;

A(a₁₁, a₁₂…a₃₂, A₃₃); Заменим каждый элемент алгебраическим дополнением. В = (A₁₁, A₁₂…A₃₂, A₃₃)*1/|A|; Транспонируем и разделим все элементы на Δ: B ^T = (A₁₁/Δ, A₂₁/Δ…A₂₃/Δ, A₃₃/Δ); B ^T =A ^-1 -?; B ^T A=E -?

(a₁₁ a₁₂…a₃₂ a₃₃)*(A₁₁A₁₂…A₃₂ A₃₃)=(a₁₁A₁₁+a₁₂A₁₂+a₁₃A₁₃/Δ)=(1 0..0 1)=E;

a₂₁A₁₁+a₂₂A₁₂+a₂₃A₁₃ = 0; a₁₁A₁₁+a₁₂A₁₂+a₁₃A₁₃=Δ;

Системы линейных алгебраических уравнений СЛАУ.

(x₁; x₂; x₃;…x_n) — матрица-столбец. A= (a₁₁ a₁₂… a_nn) * B= (b₁; b₂; … b_n); AX=B; {a₁₁ x₁+a₁₂ x₂+…+a_1n x_n = b₁; a₂₁ x₁+a₂₂ x₂+…+a_2n x_n = b₂; a_n1 x₁+a_n2 x₂+…+a_nn x_n = b_n. — ЭТО СЛАУ; Если СЛАУ имеет решение, то она называется совместной. Если это решение единственное, то СЛАУ называется определенной системой. Если СЛАУ имеет множество решений, то она называется неопределенной. Для установки совместности надо вычислить определитель: {a₁₁ x₁…+a₃₃ x₃ = b₃; Находим определитель матрицы А: Δ=|A| =|a₁₁ a₁₂…a₃₂ a₃₃| <> 0; Для совместности <=>, чтобы главный Δ системы не равнялся нулю. x1-?; Столбец коэффициента x1 занимает столбец (b) (своб. член):

Δx₁= |b₁ a₁₂ a₁₃; b₂ a₂₂…; … b₃ a₂₃ a₃₃|; Δx₂=|a₁₁ b₁ a₁₃; a₂₁ b₂ a₂₃; a₃₁ b₃ a₃₃|; Δx₃=|a₁₁ a₁₂ b₁; a₂₁ a₂₂ b₂; a₃₁ a₃₂ b₃|; x₁=Δx₁/Δ; x₂=Δx₂/Δ; x₃=Δx₃/Δ

1) Δ<>0, Δx_i<>0, тогда имеет единичное решение

2) Δ=0, Δx_i= 0, множество решений.

Определитель Вандермонда.

Для определителя Вандермонда справедлива формула

Определитель Вандермонда равен нулю, тогда и только тогда, когда среди чисел x1,…,xn есть хотя бы два одинаковых.

 

Комплексные числа.

Комплексным числом z называется выражение вида z=x+iy, где x и y – действительные числа, а i – так называемая мнимая единица, i²=-1.

Если x=0, то число 0+iy=iy называется чисто мнимым; если y=0, то число x+i0=x отождествляется с действительным числом x, а это означает, что множество R всех действительных чисел является подмножеством множества С всех комплексных чисел, т. е. RÌC.

Число x называется действительной частью комплексного числа z и обозначается x=Re z, а y – мнимой частью z, y=Im z.

Два комплексных числа z1=x1+iy1 и z2=x2+iy2 называются равными тогда и только тогда, когда равны их действительные части и равны их мнимые части: x1=x2, y1=y2. В частности, комплексное число z=x+iy равно нулю тогда и только тогда, когда x=y=0. Понятие «больше» и «меньше» для комплексных чисел не вводится.

Два комплексных числа z1=x1+iy1 и z2=x2+iy2, отличающиеся лишь знаком мнимой части, называются сопряжёнными.

Всякое комплексное число z=x+iy можно изобразить точкой M(x;y) плоскости Oxy такой, что x=Re z, y=Im z. И, наоборот, каждую точку M(x;y) координатной плоскости можно рассматривать как образ комплексного числа z=x+iy.

Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Ось абцисс называется действительной осью, так как на ней лежат действительные числа z=x+i0=x. Ось ординат называется мнимой осью, на ней лежат чисто мнимые комплексные чмсла z=0+iy.

Комплексное число z=x+iy можно задавать с помощью радиус-вектора OM=(x;y). Длина вектора OM, изображающего комплексное число z, называется модулем этого числа и обозначается |z|. Величина угла между положительным направлением действительной осью и вектором ОМ, изображающим комплексное число, называется аргументом этого комплексного числа, обозначается Arg z или j.

Аргумент комплексного числа z=0 не определён. Аргумент комплексного числа z<>0 – величина многозначная и определяется с точностью до слагаемого 2pk (k=0,-1,1,-2,2…): Arg z=arg z+2pk, где arg z – главное значение аргумента, заключённое в промежутке (-p;p].

Запись числа z в виде z=x+iy называют алгебраической формой комплексного числа.

Модуль OM и аргумент j комплексного числа можно рассматривать как полярные координаты вектора OM, изображающего комплексное число z=x+iy. Тогда получаем x=rcosj, y=rsinj, где r=OM. Следовательно, комплексное число z=x+iy можно записать в виде z=rcosj+irsinj или z=r(cosj+isinj). Такая запись комплексного числа называется тригонометрической формой. r=|z|=Ö(x²+y²).

Использую формулу Эйлера e^ij= cosj+isinj, комплексное число z=r(cosj+isinj) можно записать в так называемой показательной (или экспоненциальной) форме z=re^ij, где r=|z| - модуль комплексного числа, а угол j = Arg z=arg z+2pk.

Суммой двух комплексных чисел z1=x1+iy1 и z2=x2=iy2 называется комплексное число, определяемое равенством: z1+z2=(x1+x2)+I(y1+y2).

Сложение двух комплексных чисел обладает переместительным и сочетательным свойствами.

Геометрические комплексные числа складываются как векторы.

Вычитание определяется как действие, обратное сложению. Разностью двух комплексных чисел z1 и z2 называется такое комплексное число z, которое, будучи сложенным с z2, даёт число z1, т.е. z=z1-z2, если z+z2=z1.

Если z1=x1+iy1, z2=x2+iy2, то из этого определения легко получить z: z=z1-z2=(x1-x2)+i(y1-y2).

Геометрические комплексные числа вычитаются как векторы.

Произведением комплексных чисел z1=x1+iy1 и z2=x2+iy2 называется комплексное число, определяемое равенством: z=z1z2=(x1x2-y1y2)+i(x1y2+y1x2).

Отсюда, в частности, следует важнейшее соотношение i²=-1.

При умножении комплексных чисел их модули перемножаются, а аргументы складываются.

Это правило распространяется на любое конечное число множителей. В частности, если есть n множителей и все они одинаковые, то zⁿ=(r(cosj+isinj))ⁿ=rⁿ(cosnj+isinnj). Эта формула называется формулой Муавра.

Деление определяется как действие, обратное умножению. Частным двух комплексных чисел z1 и z2 <>0 называется комплексное число z, которое, будучи умноженное на z2, даёт число z1, т.е. z1/z2=z, если z2z=z1.

Для тригонометрической формы комплексного числа формула деления имеет вид:

При делении комплексных чисел их модули, соответственно, делятся, а аргументы, соответственно, вычитаются.

Извлечение корня n-ой степени определяется как действие, обратное возведению в натуральную степень.

Корнем n-ой степени из комплексного числа zназывается комплексное число w, удовлетворяющее равенству wⁿ=z.

Если положить z=r(cosj+isinj), а w=p(cosq+isinq), то, по определению корня и формуле Муавра, получаем z=wⁿ=pⁿ(cos(nq)+isin(nq))=r(cosj+isinj). Отсюда имеем pⁿ=r, nq=j+2pk,k=0,-1,1,-2,2,… То есть q=(j+2pk)/n и p=r^(1/n) (арифметический корень). Поэтому равенство z^(1/n)=w принимает вид:

k=0,1,…,n-1

 

Многочлены.

Комплексное число z₀ называется корнем многочлена P(z), если P(z₀)=0.

Теорема Безу. Число z₀,будет корнем многочлена P(z) степени n>=1, тогда и только тогда, когда P(z) делится на (z-z₀) без остатка.

Док-во. P(z)=H(z)(z-z₀)+R(z), где H(z) – многочлен степени (n-1), а остаток R(z) – многочлен степени 1, т.е. degR=0, т.е. R(z)=C. Итак, P(z)=(z- z₀)H(z)+C;

z= z₀, P(z₀)=0+C=C; P(z)=(z- z₀)H(z)+P(z₀)

z₀ – корень многочлена óP(z₀)=(z- z₀)H(z), т.е. P(z) делится на (z- z₀) без остатка.

Следствие. Пусть z₀ – корень многочлена P(z) степени n>=1, тогда существует натуральное число l, 1<=l<=n, такое что P(z) можно записать в виде P(z)=(z- z₀)H(z), где degH=n-l, H(z₀)<>0.

Теорема (Основная теорема алгебры). Всякий многочлен P(z) степени n>=1 имеет хотя бы один корень.

Следствие основной теоремы алгебры. Всякий многочлен P(z) степени n>=1 имеет ровно n корней с учётом их кратности и для него справедливо разложение на линейные множители. P(z)=P_n(z-z₁)^m1…(z-z_s)^ms, где z₁…z_s различные корни многочлена (z_k<>z_l при k<>l), m₁,…,m_s кратности этих корней (1<=s<=n) и m₁+…+m_s=n, P_n – старший коэффициент при Zⁿ.

Алгебра матриц.

Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаково длины (или n столбцов одинаковой длины).

Матрицы равны между собой, если равны все соответствующие элементы этих матриц.

Матрица, у которой число строк равно числу столбцов, называется квадратной.

Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.

матрица, содержащая один столбец или одну строку, называется вектором.

Матрица, полученная из данной заменой каждой её строки столбцом с тем же номером, называется матрицей  транспонированной к данной.

Суммой двух матриц A и В называется матрица С такая, что cij=aij+bij.

Разностью двух матриц A и В называется матрица С такая, что cij=aij-bij.

Произведением матрицы А на число k называется матрица В такая, что bij=k*aij.

Матрица –A=(-1)*A называется противоположной матрице А.

Разность матриц можно определить как: А-В=А+(-В).

Операции сложения матриц и умножения матрицы на число обладают следующими свойствами:

- А+В=В+А;

- A+(B+C)=(A+B)+C;

- A+0=A;

- A-A=0;

- 1*A=A;

- a*(A+B)=a*A+a*B;

- (a+b)*A=a*A+b*B

- a*(bA)=(ab)A.

Элементарные преобразования матриц:

- перестановка метами двух параллельных рядов матрицы;

- умножение всех элементов ряда матрицы на число, отличное от нуля;

- прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.

Две матрицы А и В называются эквивалентными, если одно из них получается из другой с помощью элементарных преобразований.

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

Произведением матрицы А(m´n) на матрицу В(n´p) называется матрица C(m´p) такая, что cik=ai1*b1k+ai2*b2k+…+ain*bnk, где i=1..m, k=1…p.

Матрицы А и В называются перестановочными, если АВ=ВА.

Св-ва умножения матриц:

- A(BC)=(AB)C;

- A(B+C)=AB+AC;

- (A+B)C=AC+BC;

- a(AB)= (aA)B.

Св-ва транспонирования:

- (A+B)^T=A ^T +B ^T;

- (AB) ^T=B ^T A ^T.

Пусть А – квадратная матрица n-го порядка.

При умножении квадратных матриц их определители перемножаются.

Квадратная матрица А называется невырожденной, если определитель не равен нулю, в противном случае матрица А называется вырожденной.

Матрицей, союзной к матрице А называется матрица

, где Aij – алгебраическое дополнение элемента aij данной матрицы А.

Матрица А^-1 называется обратной матрице А, если выполняется условие А*А^-1=А^-1*А=Е.

Всякая невырожденная матрица имеет обратную.

Св-ва обратных матриц:

- если у матрицы А есть обратная, то определитель А<>0;

- если В= А^-1, то А=В^-1;

- если матрица А имеет обратную, только одну;

- если А и В имеют обратные, то произведения тоже имеют обратные матрицы, причём обратная к произведению есть произведение обратных в обратном порядке (АВ) ^–1=В^-1А^-1.

Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы.

Минор, порядок которого определяет ранг матрицы, называется базисным.

Крамер. AX+ B.

Если определитель системы отличен от нуля, то система называется невырожденной.

X= А^-1B.

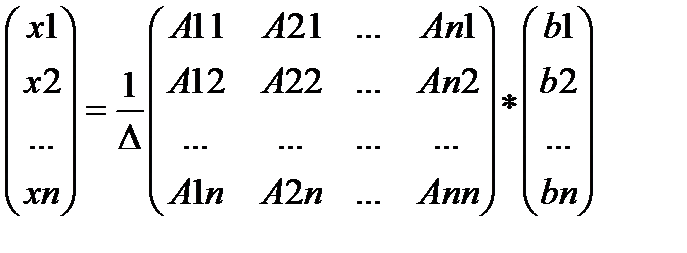
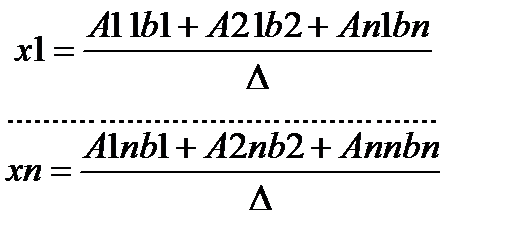
Но A11b1+A21b2+…+An1bn есть разложение определителя по элементам первого столбца.

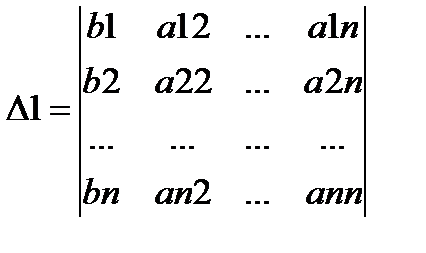
Определитель D1 получается из определителя D путём замены первого столбца коэффициентов столбцом из свободных. Итак, xi=Di/D (формула Крамера).

Линейные пространства.

Линейным пространством называется множество элементов «векторов» x,y,z,… для которых определены операции сложения векторов и умножения их на числа: x,yÎL ® z=x+yÎL; xÎL, aÎR®axÎL, причём эти операции удовлетворяют аксиомам:

1) аксиомы сложения:

· x+(y+z)=(x+y)+z (ассоциативность);

· x+y=y+x (коммутативность);

· $0ÎL: x+0=0+x=x "xÎL;

· у любого вектора есть противоположный

xÎL=>$(-x)ÎL:x+(-x)=0.

2) аксиомы умножения на число:

· 1*x=x;

· (ab)x=a(bx).

3) аксиомы дистрибутивности:

· (a+b)x=ax+bx;

· a(x+y)=ax+ay.

Примеры линейных пространств.

1. Пространство V³. Пространство геометрических векторов.

2. Пространство Rⁿ. Арифметическое пространство. Роль векторов – упорядоченные наборы из n вещественных чисел. x=(x1,x2,x3,…,xn), y=(y1,y2,y3,…,yn) и т.д.. Операции сложения векторов и умножения на число определяются покомпонентно, т.е. x+y=(x1+y1,…,xn+yn), ax=(ax1,…, axn).

3. Пространство M_mn. Роль векторов – матрицы. Сумма матриц и умножение на число поэлементно.

4. Пространство P_n. Пространство многочленов степени не выше n. Роль векторов – многочлены вида P=P(t)=p₀+p₁t+…+p_ntⁿ. Сложение векторов и умножение на число по правилам действия с многочленами.

5. Пространство функций непрерывных на отрезке С[ a _c, b _c]. Векторы – функции x=x(t), y=y(t) – непрерывные при tÎ[a_c,b_c]. Сумма векторов и умножение на число по правилам действия с функциями. x+y=x(t)+y(t), ax=ax(t).

Св-ва подпространств.

1. Если М подпространство, то 0ÎМ и для любого xÎM, => -xÎM.

Док-во. Для "xÎM имеем 0=0xÎM по определению, –x=(-1)xÎM по определению.

L=R⁴={x=(x1,x2,x3,x4),xiÎR}

M1={x=(a,0,b,0),a,bÎR}ÌR⁴

M2={x=(a,1,b,0),a,bÎR}ÌR⁴

Тогда М1 – подпространство в R⁴, а М2 не является подпространством R⁴. Для "x,yÎM1 имеем x=(a1,0,b1,0), y=(a2,0,b2,0), x+y=(a1+a2,0,b1+b2,0)ÎM1, ax=(aa1,0,ab1,0)ÎM1, значит М1 подпространство в R⁴. М2 не подпространство, например не содержит 0.

2. Подпространство линейного пространства само является линейным пространством.

Док-во. Операции сложения векторов и умножения на числа определены на всём линейном пространстве L, а значит и на МÌL, причём результаты снова в М по определению подпространства. По св-ву 1 М содержит 0 вектор и для "xÎM +> -xÎM. Все остальные аксиомы линейного пространства выполнены на всём L, а значит и на М. Вывод: М является линейным подпространством.

Вектор xÎL называется линейной комбинацией векторов из S, если существует набор чисел a1,…,akÎR такой, что x=a1x1+…+akxk.

Мн-во М=L(S) всех линейных комбинаций векторов из системы S называется линейной оболочкой системы S.

S1={a}, aÎV³; L(S1)={aa; aÎR} – все векторы, коллинеарные a.

S2={a, 2a}; L(S2)={x=a1a+a₂2a; a1,a2ÎR}={aa}=L(S1)

S3={a,b;not(a||b)}; L(S3)={x=aa+bb:a,bÎR} – мн-во всех векторов плоскости, заданной векторами a и b.

Теорема. Линейная оболочка системы векторов образует подпространство.

Док-во. Пусть S система векторов {x1,…,xk}ÌL, L(s)={x=a1x1+…+akxk: a1,…akÎR} (1). Для "x,yÎL(S) имеем в силу (1) x=a1x1+…+akxk, y=b1y1+…+bkyk; x+y=(a1+ 1)xa+…+(ak+bk)xkÎL(S)

ax=aa1x1+…+aakxkÎL(S) => L(S) подпространство в L. Замечание. L(s) есть наименьшее подпространство, содержащее все векторы системы S.

Система S={x1,…,xk} называется линейно независимой, если равенство a1x1+…+akxk=0 возможно только, когда все коэффициенты нулевые.

Системы S называется линейно зависимой, если существует не нулевой набор коэффициентов a1,…,ak<>0 (хотя бы один) для которого справедливо равенство a1x1+…+akxk=0.

Вектора

Вектор – это направленный прямолинейный отрезок, т.е. отрезок, имеющий определённую длину и определённое направление.

Длиной вектора называется длина отрезка.

Вектор, длина которого равна нулю, называется нулевым вектором.

Вектор, длина которого равна единице, называется единичным вектором.

Векторы a и b называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

Два вектора называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые длины.

Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

Вектор, соединяющий начало одного вектора с концом другого вектора называется суммой этих векторов.

Под разностью векторов a и b понимается вектор c=a-b такой, что b+c=a.

Произведением вектора a на скаляр l называется вектор lа, который имеет длину |l|*|a|, коллинеарен вектору а, имеет направление вектора а, если l>0 и противоположное, если l<0.

Линейные операции над векторами обладают следующими свойствами:

1) a+b=b+a;

2) (a+b)+c=a+(b+c);

3) l1(l2*a)= l1*l2*a;

4) (l1+l2)*a=l1*a+l2*a;

5) l(a+b)= la+lb.

Проекцией точки М на ось l называется основание М1 перпендикуляра ММ1, опущенного из точки на ось.

Проекцией вектора на AB ось l называется положительное число |AB|, если вектор A1B1 и ось l одинаково направлены и отрицательное число, если вектор А1В1 и ось l противоположно направлены.

Св-ва.

1. Проекция вектора а на ось l равна произведению модуля вектора а на косинус угла j между вектором и осью, т.е. прla=|a|*cosj.

Следствие. Проекция вектора на ось положительна(отрицательна), если вектор образует с осью острый(тупой) угол, и равна нулю, если этот угол – прямой.

Следствие. Проекции равных векторов на одну и ту же ось равны между собой.

2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось.

3. При умножении вектора а на число l его проекция на ось также умножается на это число.

Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.

 

a=ax*I+ay*j+az*k. Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных осей. Числа ax, ay, az называются координатами вектора a, т.е. координаты вектора есть его проекции на соответствующие координатные оси.

|a|=Ö(ax²+ay²+az²), т.е. модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.

cos²a+ cos²b+ cos²g=1, т.е. сумма квадратов направляющих косинусов ненулевого вектора равна единице.

Скалярным произведением двух ненулевых векторов a и b называется число, равное произведению длин этих векторов на косинус угла между ними.

Св-ва.

1) ab=ba;

2) (la)b=l(ab);

3) a(b+c)=ab+ac;

4) a²=|a|²;

5) если векторы a и b (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю.

a*b=axbx+ayby+azbz. Скалярное произведение векторов равно сумме произведений их одноимённых координат.

Векторным произведением вектора а на вектор b называется вектор с, который:

1) перпендикулярен векторам а и b;

2) имеет длину, численно равную площади параллелограмма, построенного на векторах a и b как на сторонах, т.е. |c|=|a|*|b|*sinj, где j угол между векторами а и b;

3) векторы a, b и c образуют правую тройку.

Св-ва.

1. При перестановке сомножителей векторное произведение меняет знак.

2. l(axb)=(la)xb=ax(lb).

3. Два не нулевых вектора a и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.

4. (a+b)xc=axc+bxc.

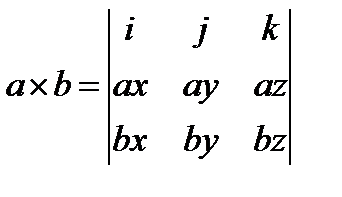
Смешанное произведение представляет собой число.

Св-ва.

1. (axb)c=(bxc)a=(cxa)b.

2. (axb)c=a(bxc).

3. Смешанное произведение меняет свой знак при перемене мест любых двух векторов-сомножителей, т.е. abc=-acb.

4. Смешанное произведение ненулевых векторов a, b и с равно нулю тогда и только тогда, когда они компланарны.

 

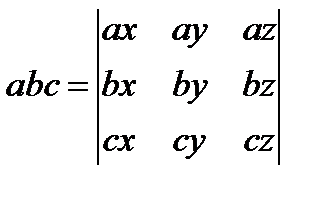
Операции над матрицами.

1. A и В считаются равными, если они имеют одинаковую размерность и соответствующие элементы равны.

2. Для того, чтобы сложить 2 матрицы, достаточно сложить соответствующие элементы.

3. Умножение матрицы на число: В = λA; достаточно умножить на это число все элементы.

4. Умножение матриц: для перемножения А и В надо выполнить следующие условия: длинна а строки матрицы А должна равняться высоте столбца матрицы В; число столбцов А = число строк В; АВ<>ВА; A (m*k) à m/k; B (k*n) à k/n; A*B = mk/kn = m/n; примеры

Определитель матрицы. Вычисляется только для квадратной матрицы. Определитель второго порядка Δ=detA=|a _ij | = a₁₁ a₂₂ — a₁₂ a₂₁; Определитель третьего порядка — число найденной по правилу Саррюса.(Примеры)

Минор и алгебраическое дополнение. Минор — это определитель, полученный вычеркиванием строки или столбца. Базисный минор — любой минор r порядка м-ы А отличный от 0. Минором Мij матрицы A, n*n, называется определитель, полученный вычеркиванием i строки и j столбца из матрицы А. Минор, взятый с определенным знаком называется алгебраическим дополнением элемента. A_ij = (-1) ^( i + j) M_ij

Разложение определителя по элементам строки или столбца.

Рассмотрим i-тую строку: Δ= a_i1 A_i1 + a_i2 A_i2 +…+a_in A_in

Рассмотрим j-тый столбец: Δ = a_1j A_1j + a_2j A_2j+…+a_nj A_nj