Если в задаче целочисленного программирования количество управляющих переменных равно двум, а ограничения имеют вид неравенств, то ее можно решить графическим методом. При этом процесс решения состоит из двух этапов.
Этап 1. Решение исходной задачи обычным графическим методом. Если найденное оптимальное решение является целочисленным, то решение прекращают. Если же найденное оптимальное решение содержит хотя бы одно дробное значение, то переходят к этапу 2.
Этап 2. В непосредственной близости от границ ОДР задачи со стороны, где расположена вершина оптимального решения нецелочисленной задачи (т.е. вблизи тех границ ОДР, куда указывает вектор градиента целевой функции), строят точки, координатами которых являются целые числа. Дальнейшее решение в точности повторяет графическое решение обычной задачи линейного программирования, с тем лишь отличием, что, продвигая в направлении вектора градиента линию уровня целевой функции, находят последнюю из целочисленных точек на пути продвижения. Именно ее координаты и будут являться оптимальным целочисленным решением исходной задачи.
ПРИМЕР: Найдите графическим методом оптимальное решение целочисленной задачи линейного программирования, заданной моделью вида:
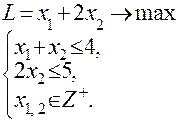
Вначале решим поставленную задачу графическим методом без ограничения на целочисленность управляющих переменных.
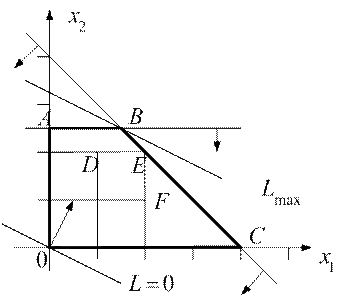
Рис. 4.
Как следует из рассмотрения рис. 4, ОДР задачи есть трапеция ОАВС, а оптимальным решением задачи будут являться координаты точки В, т.е. получено нецелочисленное оптимальное решение задачи в виде: 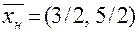 .
.
Построим внутри ОДР целочисленную сетку и примем во внимание точки D, E и F, имеющие целые значения координат. Очевидно, что наиболее близкой к точке В оказывается точка Е, координаты которой и будут являться искомым целочисленным решением: 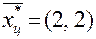 и при этом
и при этом 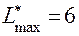 .
.
Метод Гомори решения задач целочисленного
Программирования
Для решения задач целочисленного программирования с любым количеством управляющих переменных может быть успешно применен метод Гомори. Алгоритм решения задачи этим методом содержит два этапа.
Этап 1. Решение задачи линейного программирования без условия целочисленности управляющих переменных обычным симплекс – методом. Если все значения управляющих переменных оптимального плана – целые числа, то решение заканчивают. Если же полученное оптимальное решение содержит хотя бы одно дробное значение управляющих переменных, то переходят к этапу 2.
Этап 2. Составление дополнительного ограничения (сечения) и решение расширенной задачи обычным симплекс – методом. При этом дополнительное ограничение (сечение) отсекает нецелочисленные решения, оставляя только целочисленные.
Целой частью [ r ] рационального числа r называется наибольшее целое число, не превосходящее числа r. Дробной частью числа r называется правильная дробь { r }, определяемая соотношением: { r } = r – [ r ].
Пример 1. Для числа 5 имеем: [5] = 5 и {5} = 0.
Пример 2. Для числа 4/5 имеем: [4/5] = 0 и {4/5} = 4/5.
Пример 3. Для числа 8/3 имеем: [8/3] = 2 и {8/3} = 2/3.
Пример 4. Для числа – 4/5 имеем: [- 4/5] = - 1 и {- 4/5} = 1/5.
Пример 5. Для числа – 8/3 имеем: [- 8/3] = - 3 и {- 8/3} = 1/3.
Поясним, каким образом составляется сечение (дополнительное ограничение). Пусть выполнен этап 1, т.е. найдено оптимальное решение задачи в виде:
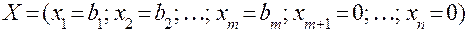
и пусть некоторое 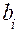 - дробное число. Рассмотрим i -ое ограничение задачи:
- дробное число. Рассмотрим i -ое ограничение задачи:

С учетом обозначений: 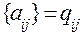 и
и 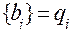 дополнительное ограничение (сечение) для переменной
дополнительное ограничение (сечение) для переменной 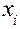 можно записать в виде:
можно записать в виде:
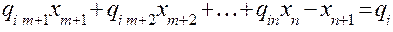 , где
, где  .
.
Очевидно, что при дополнении исходной задачи этим ограничением, получают задачу большей размерности. На практике поступают так: последнюю симплекс-таблицу, содержащую оптимальное (нецелочисленное) решение дополняют еще одной строкой с переменной 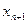 в списке базисных переменных и еще одним столбцом, соответствующим этой же дополнительной переменной, а в дополнительную строку записывают числовые коэффициенты сечения, включая значение свободного члена. После чего, обычно в одну итерацию, продолжают решение задачи симплекс – методом и, наконец, получают искомое целочисленное решение исходной задачи.
в списке базисных переменных и еще одним столбцом, соответствующим этой же дополнительной переменной, а в дополнительную строку записывают числовые коэффициенты сечения, включая значение свободного члена. После чего, обычно в одну итерацию, продолжают решение задачи симплекс – методом и, наконец, получают искомое целочисленное решение исходной задачи.
Если при решении целочисленной задачи симплекс – методом (на этапе 1) получено несколько дробных значений, то дополнительное ограничение следует составлять для значения, имеющего максимальную дробную часть.
ПРИМЕР: Найдите методом Гомори целочисленное решение задачи примера подраздела 3.3.1.
Решив поставленную задачу симплекс-методом, получим последнюю симплекс-таблицу, содержащую оптимальное (не целочисленное) решение, (убедитесь в этом сами) в виде:
| БП
| 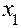
| 
| 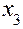
| 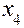
| СЧ
|

| 1
| 0
| 1
| –1/2
| 3/2
|

| 0
| 1
| 0
| 1/2
| 5/2
|
| L
| 0
| 0
| 1
| 1/2
| 13/2
|
Поскольку оба свободных члена имеют одинаковую дробную часть, равную 1/2, для определенности будем составлять сечение по Гомори для переменной  . Его можно записать в виде:
. Его можно записать в виде:
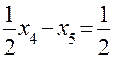 .
.
Введя это ограничение и дополнительную базисную переменную в приведенную симплекс-таблицу, получим новую симплекс-таблицу, из которой в одну итерацию получим искомое целочисленное решение поставленной задачи.
| БП
| 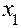
| 
| 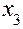
| 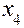
| 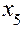
| СЧ
|

| 1
| 0
| 1
| –1/2
| 0
| 3/2
|

| 0
| 1
| 0
| 1/2
| 0
| 5/2
|
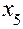
| 0
| 0
| 0
| 1/2
| –1
| 1/2
|
| L
| 0
| 0
| 1
| 1/2
| 0
| 13/2
|

| 1
| 0
| 1
| 0
| –1
| 2
|

| 0
| 1
| 0
| 0
| 1
| 2
|
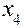
| 0
| 0
| 0
| 1
| –2
| 1
|
| L
| 0
| 0
| 1
| 0
| 1
| 6
|
Из последней симплекс-таблицы следует 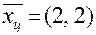 и при этом:
и при этом: 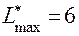 .
.
Рекомендуемая литература по теме 3: [1 ÷ 4].
ВОПРОСЫ для самопроверки знаний по теме 3:
1. Чем отличаются целочисленные задачи от обычных задач линейного программирования?
2. В чем суть графического метода решения задач целочисленного программирования?
3. В чем суть метода Гомори решения задач целочисленного программирования?
4. Для какой управляющей переменной составляется дополнительное ограничение по Гомори?



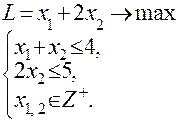

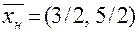 .
.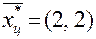 и при этом
и при этом 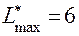 .
.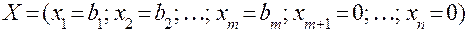
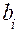 - дробное число. Рассмотрим i -ое ограничение задачи:
- дробное число. Рассмотрим i -ое ограничение задачи:
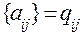 и
и 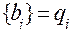 дополнительное ограничение (сечение) для переменной
дополнительное ограничение (сечение) для переменной 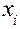 можно записать в виде:
можно записать в виде: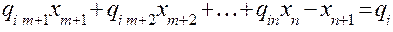 , где
, где  .
.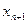 в списке базисных переменных и еще одним столбцом, соответствующим этой же дополнительной переменной, а в дополнительную строку записывают числовые коэффициенты сечения, включая значение свободного члена. После чего, обычно в одну итерацию, продолжают решение задачи симплекс – методом и, наконец, получают искомое целочисленное решение исходной задачи.
в списке базисных переменных и еще одним столбцом, соответствующим этой же дополнительной переменной, а в дополнительную строку записывают числовые коэффициенты сечения, включая значение свободного члена. После чего, обычно в одну итерацию, продолжают решение задачи симплекс – методом и, наконец, получают искомое целочисленное решение исходной задачи.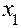

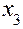
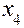

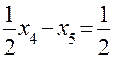 .
.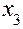
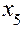
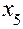
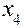
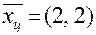 и при этом:
и при этом: 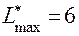 .
.


