При a = 0 уравнение (3.1) принимает вид:
5x2 + 4xy + 2y2 + 8x - 6y + 5 = 0 (3.2)
Приведем уравнение кривой (3.2) к каноническому виду, применяя преобразования параллельного переноса и поворота координатных осей. Мы установили, что данная кривая — центральная, поэтому используем методику приведения к каноническому виду для уравнения центральной кривой.
a) Характеристическое уравнения для данной кривой будет иметь вид:
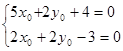
A(x, y) = 5x2 + 4xy + 2y2

Откуда следует, корни характеристического уравнения есть: l1 = 1, l2 = 6.
Расположение эллипса относительно начальной системы координат будет известно, если мы будем знать координаты центра и угловой коэффициент вещественной оси эллипса.
Уравнения для определения координат центра имеют вид:
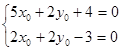
Откуда мы находим x0 = -  и y0 =
и y0 =  . Следовательно, точка O ¢ (-
. Следовательно, точка O ¢ (-  ,
,  ) есть центр данной кривой.
) есть центр данной кривой.
Угловой коэффициент оси O ¢ X можем определить по формуле:

б) Совершим параллельный перенос начала координат в точку O ¢ (x0, y0). При этом координаты x, yпроизвольной точки плоскости в системе координат xOy и координаты x ', y ' в новой системе координат x ' O ' y ' связаны соотношениями:

Подставив данные выражения в уравнение (3.1), получим:
5(x0 + x¢)2 + 4(x0 + x¢)(y0 + y¢) + 2(y0 + y¢)2 + 8(x0 + x¢) - 6(y0 + y¢) + 5=0
Раскрыв скобки и приведя подобные члены, получим:
5x¢2+4x¢y¢+2y¢2+(10x0+4x0 + 8)x¢ + (4x0 + 4y0 - 6)y¢ + (5x02 + 4x0y0 + 2y02 + 8x0 - 6y0 + 5) = 0 (3.3)
В данном уравнении коэффициенты при x¢ и y¢ приравняем к нулю и получим систему уравнений:

Решив эту систему уравнений, мы получим, найденные уже раннее, координаты центра O ¢, x0 = -  и y0 =
и y0 =  . Подставив данные значения в уравнение (3.3), коэффициенты при x¢ и y¢ станут равными нулю, мы получим уравнение в системе координат x ' O ' y ':
. Подставив данные значения в уравнение (3.3), коэффициенты при x¢ и y¢ станут равными нулю, мы получим уравнение в системе координат x ' O ' y ':
5x¢2 + 4x¢y¢ + 2y¢2 + (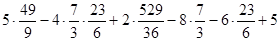 ) = 0
) = 0
5x¢2 + 4x¢y¢ + 2y¢2 - 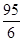 = 0 (3.4)
= 0 (3.4)
в) Так как a12 = 2 ¹ 0, то для дальнейшего упрощения необходимо произвести поворота осей координат на угол a. При повороте осей координат на угол a координаты x', y' произвольной точки М плоскости в системе координат x ' O ' y ' и координаты X, Y в новой системе координат XO'Y связаны соотношениями:

Подставим данные выражения в уравнение (3.4), получим:
5(Xcosa - Ysina)2 + 4(Xcosa - Ysina)(Xsina + Ycosa) + 2(Xsina + Ycosa)2 -  = 0
= 0
(5cos2a + 4sinacosa + 2sin2a)X2 + (-6sinacosa + 4cos2a - 4sin2a)XY +
(5sin2a - 4sinacosa + 2cos2a)Y2 - 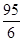 = 0 (3.5)
= 0 (3.5)
В полученном выражении найдём такой угол a, чтобы коэффициент при XY стал равен нулю, для этого необходимо:
-6sinacosa + 4cos2a - 4sin2a = 0
2tg2a + 3tga - 2=0
Откуда, при решении, находим два значения tga = -2 и tga =  .
.
В первом задании мы нашли, что угловой коэффициент вещественной оси O ' X эллипса равен k = -2. Так как угловой коэффициент равен тангенсу, то из двух найдённых значений выберем tga = -2. Следовательно:
cosa =  , sina =
, sina = 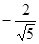
Подставив данные значения для sina и cosa в уравнение (3.5), коэффициент при XY станет равным нулю, получим:
( )X2 + (
)X2 + ( )Y2 -
)Y2 - 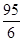 = 0
= 0
X2 + 6Y2 - 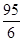 = 0
= 0
 (3.6)
(3.6)
- это каноническое уравнение данной кривой (3.1) при a = 0.
Построение графиков
Подтвердим результаты проведённого исследования данного уравнения кривой (3.1) второго порядка, построив соответствующие графики кривых при разных a.
При a = 3 уравнение (3.1) принимает вид:
2x2 + 4xy + 3y2 + 8x – 6y +5 = 0
Графиком данного уравнения является парабола:
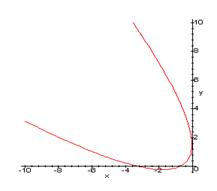
При a = 6 уравнение (3.1) принимает вид:
x2 + 4xy + 3y2 + 8y2 – 6y +5 = 0
Графиком данного уравнения является гипербола:
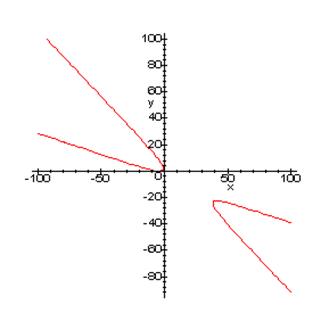
При a = 0 уравнение (3.1) принимает вид
5x2 + 4xy + 3y2 + 8y2 – 6y +5 = 0
Графиком данного уравнения является эллипс. Изобразим в данной системе также график канонического уравнения эллипса (3.6):
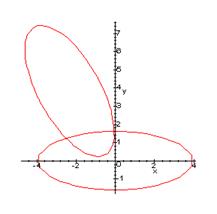
Вывод
Исследовав данное общее уравнение кривой второго порядка, мы установили, что при значении параметра a = 0 уравнение задаёт эллипс. Привели уравнение к каноническому виду, применяя преобразования параллельного переноса и поворота. При параллельном переносе коэффициенты при первых степенях стали равны нулю, при повороте координатных осей коэффициенты при смешанном произведении стали равны нулю. Построили графики для всех фигур, которое может задавать данное уравнение, построили график эллипса в общей и канонической системе координат.



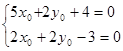

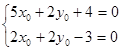
 и y0 =
и y0 =  . Следовательно, точка O ¢ (-
. Следовательно, точка O ¢ (-  ,
,  ) есть центр данной кривой.
) есть центр данной кривой.


 . Подставив данные значения в уравнение (3.3), коэффициенты при x¢ и y¢ станут равными нулю, мы получим уравнение в системе координат x ' O ' y ':
. Подставив данные значения в уравнение (3.3), коэффициенты при x¢ и y¢ станут равными нулю, мы получим уравнение в системе координат x ' O ' y ':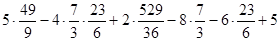 ) = 0
) = 0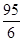 = 0 (3.4)
= 0 (3.4)
 = 0
= 0 .
. , sina =
, sina = 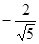
 )X2 + (
)X2 + ( )Y2 -
)Y2 -  (3.6)
(3.6)





