Интегральное исчисление.
В дифференциальном исчислении определено понятие производной в точке. Можно сказать, что это предел некоей взвешенной разности:

Если производную взять в каждой точке, то возникнет новая функция y ´(x). Итак, имеется некий алгоритм перехода y 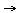 y ´. Естественным образом возникает вопрос о нахождении функции по её производной: y ´
y ´. Естественным образом возникает вопрос о нахождении функции по её производной: y ´ 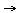 y. Возникает идея: если производная является как бы разностью, то обратный переход должен осуществляться с помощью суммирования.
y. Возникает идея: если производная является как бы разностью, то обратный переход должен осуществляться с помощью суммирования.
Рассмотрим эту идею более подробно. Пусть на отрезке [a; b] задана функция y ´(x). Требуется восстановить функцию y (x) такую, что её производная даёт y ´(x). Сразу отметим, что y (x) определяется неоднозначно. По свойству производной y (x) + c имеет ту же производную, что и y (x). По этой причине можем считать, что y (a) = y 0. Разобьём отрезок [a; x] на n частей длины 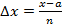 . Обозначим
. Обозначим  , тогда
, тогда
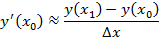
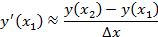
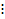
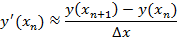
Далее  . Итак,
. Итак, 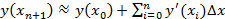 .
.
Чтобы получить точное выражение y (x) нужно устремить 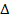 x к нулю. Тогда сумма ∑ превратится в сумму бесконечного ряда. Она обозначается через
x к нулю. Тогда сумма ∑ превратится в сумму бесконечного ряда. Она обозначается через 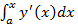 (интеграл). Рассмотрим, каков геометрический смысл интеграла. У нас задана функция y ´(x), то произведение
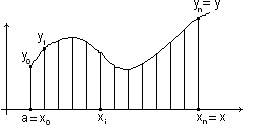
(интеграл). Рассмотрим, каков геометрический смысл интеграла. У нас задана функция y ´(x), то произведение 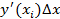 приблизительно равно площади полоски шириной
приблизительно равно площади полоски шириной 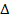 x.
x.
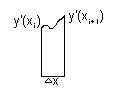 Тогда сумма равна площади криволинейной трапеции на отрезке [a; x]. Итак, задача нахождения функции по её производной связана с вычислением предела некоторой суммы (с увеличением числа членов), т. е. интеграла. Геометрический смысл интеграла состоит в том, что он выражает площадь криволинейной трапеции. Таким образом, задача о проведении касательной и задача о вычислении площадей являются обратными друг к другу.
Тогда сумма равна площади криволинейной трапеции на отрезке [a; x]. Итак, задача нахождения функции по её производной связана с вычислением предела некоторой суммы (с увеличением числа членов), т. е. интеграла. Геометрический смысл интеграла состоит в том, что он выражает площадь криволинейной трапеции. Таким образом, задача о проведении касательной и задача о вычислении площадей являются обратными друг к другу.
Мы установим, что 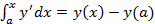 . Фактически в этом и состоит основной результат интегрального исчисления. Полученная формула называется формулой Ньютона-Лейбница.
. Фактически в этом и состоит основной результат интегрального исчисления. Полученная формула называется формулой Ньютона-Лейбница.
Перейдем к более точным определениям.
Пусть 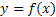 – некоторая функция, тогда функция F(x) такая, что
– некоторая функция, тогда функция F(x) такая, что 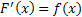 называется неопределенным интегралом или первообразной для f(x) и обозначается
называется неопределенным интегралом или первообразной для f(x) и обозначается 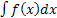 .
.
Задачу нахождения первообразной можно в ряде случаев решить с помощью таблицы производных. Например, из формулы дифференцирования функции 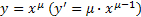 вытекает, что
вытекает, что 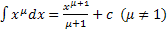 .
.
1. 
2. 
3. 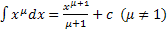
4. 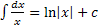
5. 
6. 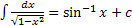
7. 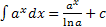
8. 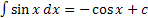
9. 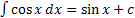
10. 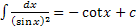
11. 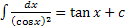
12. 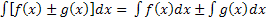
13. 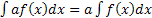
14. Если 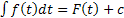 , то
, то 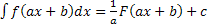
Интегрирование путем замены переменной
Теорема. Если 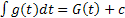 , то
, то 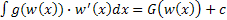 .
.
Пример 1.
 . Положим
. Положим 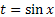 , тогда
, тогда 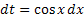 .
.
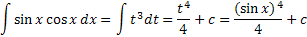
Пример 2.

Пример 3.
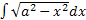 . Положим
. Положим 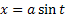 , тогда
, тогда 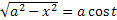 . Далее
. Далее 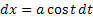 .
. 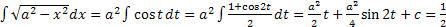 . Далее
. Далее  ,
, 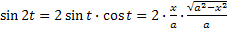 . В итоге
. В итоге 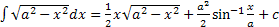 .
.
Одним из важных признаков применения замены переменной является наличие производной и функции. Например, 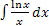 содержит
содержит 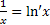 логарифм.
логарифм. 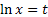
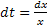 , следовательно,
, следовательно, 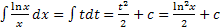 .
.
Особое значение играют методы интегрирования рациональных функций вида 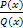 , где P(x) и Q(x) – многочлены. Общая схема интегрирования такова:
, где P(x) и Q(x) – многочлены. Общая схема интегрирования такова:
1. Если дробь 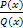 не является правильной, то можно выполнить деление и разбить дробь на сумму многочлена и правильной дроби, т.е. дроби, у которой степень числителя меньше степени знаменателя.
не является правильной, то можно выполнить деление и разбить дробь на сумму многочлена и правильной дроби, т.е. дроби, у которой степень числителя меньше степени знаменателя.
2. Если дробь 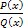 является правильной, то ее можно разложить на сумму простых дробей, т.е. дробей вида
является правильной, то ее можно разложить на сумму простых дробей, т.е. дробей вида 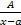 ,
, 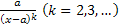 ,
, 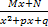 ,
, 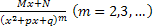 . Чтобы выполнить это разложение, необходимо разложить на множители знаменатель Q(x), что само по себе является сложной задачей. Затем применяется метод неопределенных коэффициентов.
. Чтобы выполнить это разложение, необходимо разложить на множители знаменатель Q(x), что само по себе является сложной задачей. Затем применяется метод неопределенных коэффициентов.
3. Интегралы от простых дробей выражаются с помощью логарифмов и арктангенсов.
Пример.
Дробь 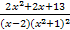 представляют в виде
представляют в виде 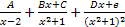 . Далее складывают простые дроби и приравнивают друг другу коэффициенты многочленов. В результате возникает система линейных уравнений относительно A, B, C, D, E. Результат
. Далее складывают простые дроби и приравнивают друг другу коэффициенты многочленов. В результате возникает система линейных уравнений относительно A, B, C, D, E. Результат 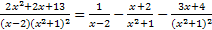 .
.
Интегралы вида 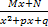 и
и 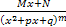 вычисляются следующим образом:
вычисляются следующим образом: 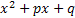 выделением полного квадрата представляют в виде
выделением полного квадрата представляют в виде 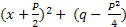 . Далее полагают
. Далее полагают 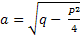 и делают подстановку
и делают подстановку  ,
, 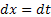 ,
, 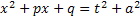 ,
, 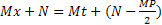 .
.
Интегрирование по частям
Поскольку 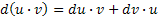 ,
, 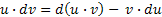 . Интегрируя обе части, получим
. Интегрируя обе части, получим 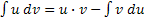 .
.
Пример.
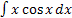 . Положим
. Положим 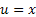 ,
,  ,
, 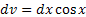 . Тогда
. Тогда 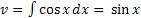 . Следовательно,
. Следовательно, 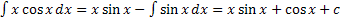 .
.
В отличие от дифференцирования, интегрирование требует значительных творческих усилий. При этом оказывается, что не все функции, выражаемые через элементарные, имеют интеграл, выражаемый через элементарные функции. Так, например, 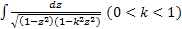 называется эллиптическим интегралом 1-го рода и взять его невозможно.
называется эллиптическим интегралом 1-го рода и взять его невозможно.
Благодаря этому в математическом анализе появляются новые функции. Их изучение затруднено, но возможно разложение этих функций в ряды и т. д.
Определенный интеграл
Для вычисления площадей криволинейных трапеций вводится понятие определенного интеграла. Интуитивно он является пределом суммы площадей малых прямоугольников при стремлении максимальной ширины прямоугольника к нулю. Согласно обозначениям Лейбница интеграл записывается следующим образом: 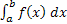 .
.
Смысл этого обозначения прост: знак ∫ – стилизованная буква S символизирует сумму. Буквы a и b указывают отрезок, на котором проводится суммирование. Они называются пределами интегрирования. Произведение  выражает площадь бесконечно узкого прямоугольника. Таким образом, речь идет о сумме площадей таких прямоугольников.
выражает площадь бесконечно узкого прямоугольника. Таким образом, речь идет о сумме площадей таких прямоугольников.
Интегрального исчисления.
Пусть функция f (x) интегрируема на отрезке [ a, b ]. Рассмотрим функцию 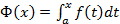 . Придадим аргументу x приращение
. Придадим аргументу x приращение 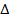 x. Тогда
x. Тогда 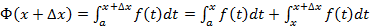 . Второй интеграл при стремлении
. Второй интеграл при стремлении 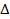 x к нулю приближённо равен площади f (x)
x к нулю приближённо равен площади f (x) 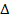 x, таким образом,
x, таким образом, 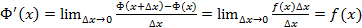 . Итак, Ф(x) – первообразная функции f (x). Пусть F (x) – любая другая первообразная той же функции. Тогда Ф (x)= F (x)+ c. Определим с. Ф (a)=0, значит, 0= Ф (а)= F (a)+ c, т.е. c =- F (a). Окончательно Ф (x)= F (x)- F (a). При x = b получаем формулу Ньютона-Лейбница:
. Итак, Ф(x) – первообразная функции f (x). Пусть F (x) – любая другая первообразная той же функции. Тогда Ф (x)= F (x)+ c. Определим с. Ф (a)=0, значит, 0= Ф (а)= F (a)+ c, т.е. c =- F (a). Окончательно Ф (x)= F (x)- F (a). При x = b получаем формулу Ньютона-Лейбница:
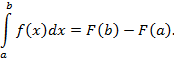
Пример. Найти площадь одной арки синусоиды ( на отрезке [0, π].)
на отрезке [0, π].)
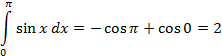
Несобственные интегралы
1. Несобственные интегралы с бесконечными приделами. Пусть функция y = f(x) определена на [a, + 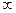 ) и имеет смысл
) и имеет смысл 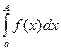 для любого A > a. Тогда по определению
для любого A > a. Тогда по определению 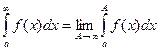 . Аналогично определяется
. Аналогично определяется 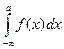 , а
, а 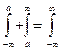 .
.
Пример. 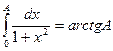 , откуда
, откуда 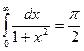 и
и 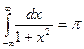 .
.
Важнейшую роль эти интегралы играют в теории вероятностей.
2. Несобственные интегралы от неограниченных функций.
Пусть 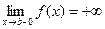 , но при любом η > 0 существует
, но при любом η > 0 существует 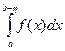 , тогда
, тогда 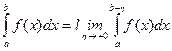 .
.
Пример.  , откуда следует, что
, откуда следует, что 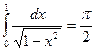 .
.
Интегральное исчисление.
В дифференциальном исчислении определено понятие производной в точке. Можно сказать, что это предел некоей взвешенной разности:

Если производную взять в каждой точке, то возникнет новая функция y ´(x). Итак, имеется некий алгоритм перехода y 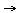 y ´. Естественным образом возникает вопрос о нахождении функции по её производной: y ´
y ´. Естественным образом возникает вопрос о нахождении функции по её производной: y ´ 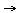 y. Возникает идея: если производная является как бы разностью, то обратный переход должен осуществляться с помощью суммирования.
y. Возникает идея: если производная является как бы разностью, то обратный переход должен осуществляться с помощью суммирования.
Рассмотрим эту идею более подробно. Пусть на отрезке [a; b] задана функция y ´(x). Требуется восстановить функцию y (x) такую, что её производная даёт y ´(x). Сразу отметим, что y (x) определяется неоднозначно. По свойству производной y (x) + c имеет ту же производную, что и y (x). По этой причине можем считать, что y (a) = y 0. Разобьём отрезок [a; x] на n частей длины 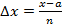 . Обозначим
. Обозначим  , тогда
, тогда
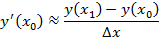
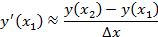
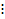
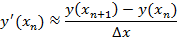

Далее  . Итак,
. Итак, 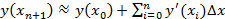 .
.
Чтобы получить точное выражение y (x) нужно устремить 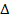 x к нулю. Тогда сумма ∑ превратится в сумму бесконечного ряда. Она обозначается через
x к нулю. Тогда сумма ∑ превратится в сумму бесконечного ряда. Она обозначается через 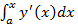 (интеграл). Рассмотрим, каков геометрический смысл интеграла. У нас задана функция y ´(x), то произведение
(интеграл). Рассмотрим, каков геометрический смысл интеграла. У нас задана функция y ´(x), то произведение 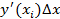 приблизительно равно площади полоски шириной
приблизительно равно площади полоски шириной 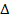 x.
x.
 Тогда сумма равна площади криволинейной трапеции на отрезке [a; x]. Итак, задача нахождения функции по её производной связана с вычислением предела некоторой суммы (с увеличением числа членов), т. е. интеграла. Геометрический смысл интеграла состоит в том, что он выражает площадь криволинейной трапеции. Таким образом, задача о проведении касательной и задача о вычислении площадей являются обратными друг к другу.
Тогда сумма равна площади криволинейной трапеции на отрезке [a; x]. Итак, задача нахождения функции по её производной связана с вычислением предела некоторой суммы (с увеличением числа членов), т. е. интеграла. Геометрический смысл интеграла состоит в том, что он выражает площадь криволинейной трапеции. Таким образом, задача о проведении касательной и задача о вычислении площадей являются обратными друг к другу.
Мы установим, что 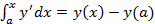 . Фактически в этом и состоит основной результат интегрального исчисления. Полученная формула называется формулой Ньютона-Лейбница.
. Фактически в этом и состоит основной результат интегрального исчисления. Полученная формула называется формулой Ньютона-Лейбница.
Перейдем к более точным определениям.
Пусть 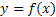 – некоторая функция, тогда функция F(x) такая, что
– некоторая функция, тогда функция F(x) такая, что 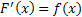 называется неопределенным интегралом или первообразной для f(x) и обозначается
называется неопределенным интегралом или первообразной для f(x) и обозначается 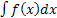 .
.
Задачу нахождения первообразной можно в ряде случаев решить с помощью таблицы производных. Например, из формулы дифференцирования функции 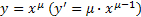 вытекает, что
вытекает, что 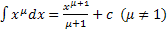 .
.
1. 
2. 
3. 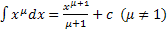
4. 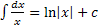
5. 
6. 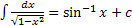
7. 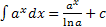
8. 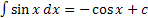
9. 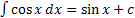
10. 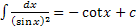
11. 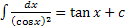
12. 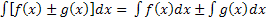
13. 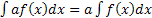
14. Если 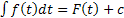 , то
, то 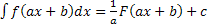
Интегрирование путем замены переменной
Теорема. Если 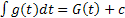 , то
, то 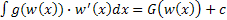 .
.
Пример 1.
 . Положим
. Положим 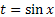 , тогда
, тогда 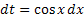 .
.
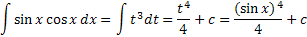
Пример 2.

Пример 3.
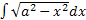 . Положим
. Положим 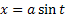 , тогда
, тогда 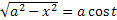 . Далее
. Далее 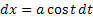 .
. 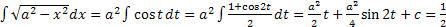 . Далее
. Далее  ,
, 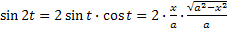 . В итоге
. В итоге 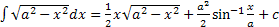 .
.
Одним из важных признаков применения замены переменной является наличие производной и функции. Например, 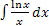 содержит
содержит 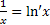 логарифм.
логарифм. 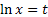
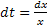 , следовательно,
, следовательно, 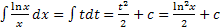 .
.
Особое значение играют методы интегрирования рациональных функций вида 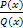 , где P(x) и Q(x) – многочлены. Общая схема интегрирования такова:
, где P(x) и Q(x) – многочлены. Общая схема интегрирования такова:
1. Если дробь 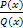 не является правильной, то можно выполнить деление и разбить дробь на сумму многочлена и правильной дроби, т.е. дроби, у которой степень числителя меньше степени знаменателя.
не является правильной, то можно выполнить деление и разбить дробь на сумму многочлена и правильной дроби, т.е. дроби, у которой степень числителя меньше степени знаменателя.
2. Если дробь 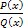 является правильной, то ее можно разложить на сумму простых дробей, т.е. дробей вида
является правильной, то ее можно разложить на сумму простых дробей, т.е. дробей вида 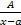 ,
, 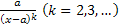 ,
, 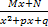 ,
, 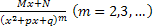 . Чтобы выполнить это разложение, необходимо разложить на множители знаменатель Q(x), что само по себе является сложной задачей. Затем применяется метод неопределенных коэффициентов.
. Чтобы выполнить это разложение, необходимо разложить на множители знаменатель Q(x), что само по себе является сложной задачей. Затем применяется метод неопределенных коэффициентов.
3. Интегралы от простых дробей выражаются с помощью логарифмов и арктангенсов.
Пример.
Дробь 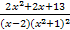 представляют в виде
представляют в виде 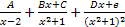 . Далее складывают простые дроби и приравнивают друг другу коэффициенты многочленов. В результате возникает система линейных уравнений относительно A, B, C, D, E. Результат
. Далее складывают простые дроби и приравнивают друг другу коэффициенты многочленов. В результате возникает система линейных уравнений относительно A, B, C, D, E. Результат 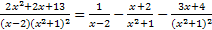 .
.
Интегралы вида 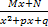 и
и 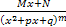 вычисляются следующим образом:
вычисляются следующим образом: 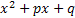 выделением полного квадрата представляют в виде
выделением полного квадрата представляют в виде 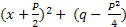 . Далее полагают
. Далее полагают 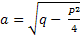 и делают подстановку
и делают подстановку  ,
, 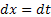 ,
, 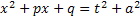 ,
, 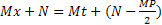 .
.
Интегрирование по частям
Поскольку 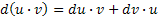 ,
, 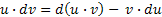 . Интегрируя обе части, получим
. Интегрируя обе части, получим 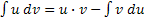 .
.
Пример.
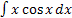 . Положим
. Положим 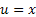 ,
,  ,
, 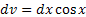 . Тогда
. Тогда 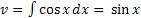 . Следовательно,
. Следовательно, 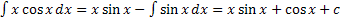 .
.
В отличие от дифференцирования, интегрирование требует значительных творческих усилий. При этом оказывается, что не все функции, выражаемые через элементарные, имеют интеграл, выражаемый через элементарные функции. Так, например, 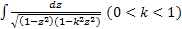 называется эллиптическим интегралом 1-го рода и взять его невозможно.
называется эллиптическим интегралом 1-го рода и взять его невозможно.
Благодаря этому в математическом анализе появляются новые функции. Их изучение затруднено, но возможно разложение этих функций в ряды и т. д.
Определенный интеграл
Для вычисления площадей криволинейных трапеций вводится понятие определенного интеграла. Интуитивно он является пределом суммы площадей малых прямоугольников при стремлении максимальной ширины прямоугольника к нулю. Согласно обозначениям Лейбница интеграл записывается следующим образом: 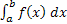 .
.
Смысл этого обозначения прост: знак ∫ – стилизованная буква S символизирует сумму. Буквы a и b указывают отрезок, на котором проводится суммирование. Они называются пределами интегрирования. Произведение  выражает площадь бесконечно узкого прямоугольника. Таким образом, речь идет о сумме площадей таких прямоугольников.
выражает площадь бесконечно узкого прямоугольника. Таким образом, речь идет о сумме площадей таких прямоугольников.




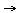 y ´. Естественным образом возникает вопрос о нахождении функции по её производной: y ´
y ´. Естественным образом возникает вопрос о нахождении функции по её производной: y ´ 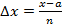 . Обозначим
. Обозначим  , тогда
, тогда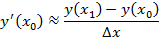
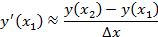
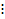
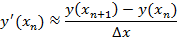

 . Итак,
. Итак, 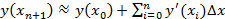 .
.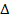 x к нулю. Тогда сумма ∑ превратится в сумму бесконечного ряда. Она обозначается через
x к нулю. Тогда сумма ∑ превратится в сумму бесконечного ряда. Она обозначается через 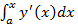 (интеграл). Рассмотрим, каков геометрический смысл интеграла. У нас задана функция y ´(x), то произведение
(интеграл). Рассмотрим, каков геометрический смысл интеграла. У нас задана функция y ´(x), то произведение 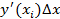 приблизительно равно площади полоски шириной
приблизительно равно площади полоски шириной 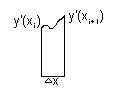 Тогда сумма равна площади криволинейной трапеции на отрезке [a; x]. Итак, задача нахождения функции по её производной связана с вычислением предела некоторой суммы (с увеличением числа членов), т. е. интеграла. Геометрический смысл интеграла состоит в том, что он выражает площадь криволинейной трапеции. Таким образом, задача о проведении касательной и задача о вычислении площадей являются обратными друг к другу.
Тогда сумма равна площади криволинейной трапеции на отрезке [a; x]. Итак, задача нахождения функции по её производной связана с вычислением предела некоторой суммы (с увеличением числа членов), т. е. интеграла. Геометрический смысл интеграла состоит в том, что он выражает площадь криволинейной трапеции. Таким образом, задача о проведении касательной и задача о вычислении площадей являются обратными друг к другу.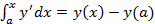 . Фактически в этом и состоит основной результат интегрального исчисления. Полученная формула называется формулой Ньютона-Лейбница.
. Фактически в этом и состоит основной результат интегрального исчисления. Полученная формула называется формулой Ньютона-Лейбница.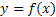 – некоторая функция, тогда функция F(x) такая, что
– некоторая функция, тогда функция F(x) такая, что 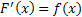 называется неопределенным интегралом или первообразной для f(x) и обозначается
называется неопределенным интегралом или первообразной для f(x) и обозначается 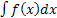 .
.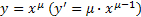 вытекает, что
вытекает, что 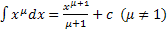 .
.

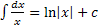

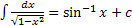
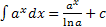
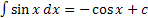
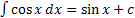
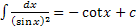
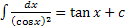
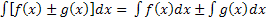
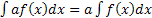
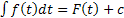 , то
, то 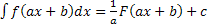
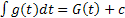 , то
, то 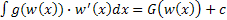 .
. . Положим
. Положим 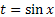 , тогда
, тогда 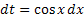 .
.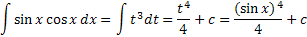

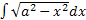 . Положим
. Положим 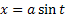 , тогда
, тогда 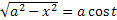 . Далее
. Далее 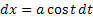 .
. 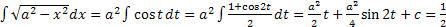 . Далее
. Далее  ,
, 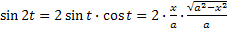 . В итоге
. В итоге 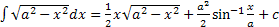 .
.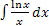 содержит
содержит 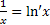 логарифм.
логарифм. 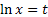
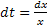 , следовательно,
, следовательно, 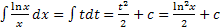 .
.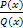 , где P(x) и Q(x) – многочлены. Общая схема интегрирования такова:
, где P(x) и Q(x) – многочлены. Общая схема интегрирования такова: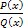 является правильной, то ее можно разложить на сумму простых дробей, т.е. дробей вида
является правильной, то ее можно разложить на сумму простых дробей, т.е. дробей вида 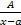 ,
, 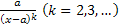 ,
, 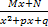 ,
, 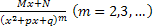 . Чтобы выполнить это разложение, необходимо разложить на множители знаменатель Q(x), что само по себе является сложной задачей. Затем применяется метод неопределенных коэффициентов.
. Чтобы выполнить это разложение, необходимо разложить на множители знаменатель Q(x), что само по себе является сложной задачей. Затем применяется метод неопределенных коэффициентов.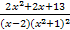 представляют в виде
представляют в виде 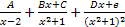 . Далее складывают простые дроби и приравнивают друг другу коэффициенты многочленов. В результате возникает система линейных уравнений относительно A, B, C, D, E. Результат
. Далее складывают простые дроби и приравнивают друг другу коэффициенты многочленов. В результате возникает система линейных уравнений относительно A, B, C, D, E. Результат 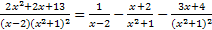 .
.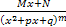 вычисляются следующим образом:
вычисляются следующим образом: 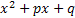 выделением полного квадрата представляют в виде
выделением полного квадрата представляют в виде 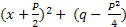 . Далее полагают
. Далее полагают 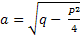 и делают подстановку
и делают подстановку  ,
, 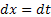 ,
, 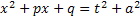 ,
, 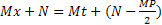 .
.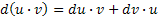 ,
, 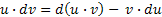 . Интегрируя обе части, получим
. Интегрируя обе части, получим 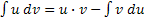 .
.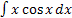 . Положим
. Положим 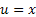 ,
,  ,
, 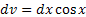 . Тогда
. Тогда 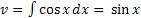 . Следовательно,
. Следовательно, 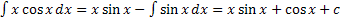 .
.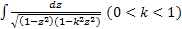 называется эллиптическим интегралом 1-го рода и взять его невозможно.
называется эллиптическим интегралом 1-го рода и взять его невозможно.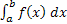 .
. выражает площадь бесконечно узкого прямоугольника. Таким образом, речь идет о сумме площадей таких прямоугольников.
выражает площадь бесконечно узкого прямоугольника. Таким образом, речь идет о сумме площадей таких прямоугольников.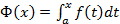 . Придадим аргументу x приращение
. Придадим аргументу x приращение 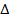 x. Тогда
x. Тогда 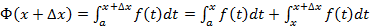 . Второй интеграл при стремлении
. Второй интеграл при стремлении 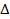 x к нулю приближённо равен площади f (x)
x к нулю приближённо равен площади f (x) 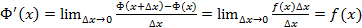 . Итак, Ф(x) – первообразная функции f (x). Пусть F (x) – любая другая первообразная той же функции. Тогда Ф (x)= F (x)+ c. Определим с. Ф (a)=0, значит, 0= Ф (а)= F (a)+ c, т.е. c =- F (a). Окончательно Ф (x)= F (x)- F (a). При x = b получаем формулу Ньютона-Лейбница:
. Итак, Ф(x) – первообразная функции f (x). Пусть F (x) – любая другая первообразная той же функции. Тогда Ф (x)= F (x)+ c. Определим с. Ф (a)=0, значит, 0= Ф (а)= F (a)+ c, т.е. c =- F (a). Окончательно Ф (x)= F (x)- F (a). При x = b получаем формулу Ньютона-Лейбница: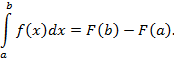
 на отрезке [0, π].)
на отрезке [0, π].)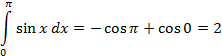
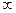 ) и имеет смысл
) и имеет смысл 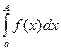 для любого A > a. Тогда по определению
для любого A > a. Тогда по определению 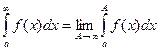 . Аналогично определяется
. Аналогично определяется 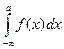 , а
, а 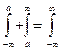 .
.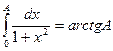 , откуда
, откуда 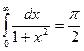 и
и 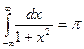 .
.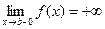 , но при любом η > 0 существует
, но при любом η > 0 существует 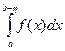 , тогда
, тогда 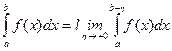 .
. , откуда следует, что
, откуда следует, что 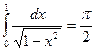 .
.


