

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...
Топ:
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности...
Интересное:
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Ковариация случайных величин 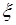 и
и  определяется через их совместную плотность вероятности
определяется через их совместную плотность вероятности 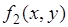 соотношением:
соотношением:
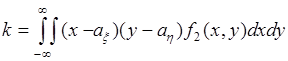 . (57.1)
. (57.1)
Подынтегральная функция в (57.1) неотрицательна для таких 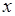 ,
, 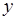 , при которых
, при которых 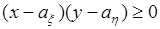 , то есть при
, то есть при 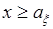 ,
, 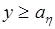 или
или 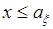 ,
, 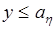 . И наоборот, при
. И наоборот, при 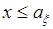 ,
, 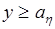 или
или 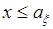 ,
, 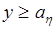 подынтегральная функция (57.1) отрицательна либо равна нулю. Знак ковариации зависит от того, какие значения, положительные или отрицательные преобладают в подынтегральной функции. Поэтому знак числа
подынтегральная функция (57.1) отрицательна либо равна нулю. Знак ковариации зависит от того, какие значения, положительные или отрицательные преобладают в подынтегральной функции. Поэтому знак числа 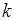 определяется расположением линий равного уровня плотности вероятности
определяется расположением линий равного уровня плотности вероятности  . На рис. 57.1 представлен пример линий равного уровня функции
. На рис. 57.1 представлен пример линий равного уровня функции 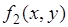 , для которой
, для которой 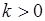 . Штриховкой
. Штриховкой
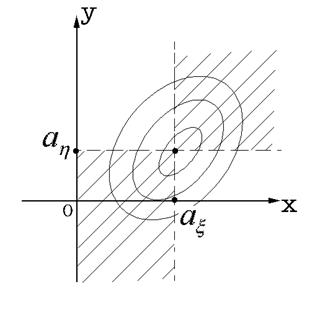
Рис. 57.1.
Линии равного уровня плотности вероятности при 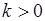 .указана часть плоскости, на которой
.указана часть плоскости, на которой 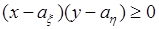 , и следовательно неотрицательна подынтегральная функция. Поскольку в заштрихованной области (положительные значения подынтегральной функции) плотность
, и следовательно неотрицательна подынтегральная функция. Поскольку в заштрихованной области (положительные значения подынтегральной функции) плотность  имеет в среднем большее значение, чем в нештрихованной области (отрицательные значения подынтегральной функции), то ковариация
имеет в среднем большее значение, чем в нештрихованной области (отрицательные значения подынтегральной функции), то ковариация  . На рис. 57.2 представлены линии равного уровня плотности
. На рис. 57.2 представлены линии равного уровня плотности  при
при 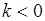 . Случай
. Случай 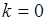 соответствует симметричному расположению линий относительно прямой
соответствует симметричному расположению линий относительно прямой 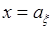 (или
(или 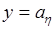 ). Например, эти линии могут быть эллипсами, у которых большая полуось совпадает по направлению с прямой
). Например, эти линии могут быть эллипсами, у которых большая полуось совпадает по направлению с прямой 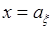 (или
(или 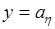 ). Другой пример – линии являются окружностями с центром в точке
). Другой пример – линии являются окружностями с центром в точке 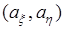 .
.
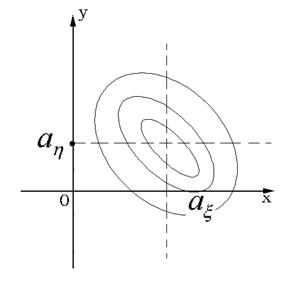
Рис. 57.2. Линии равного уровня плотности
вероятности при 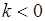 .
.
Отметим, что если 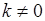 , а линии равного уровня имеют ось симметрии, например, на рис. 57.1 линии – это эллипсы, тогда можно выполнить преобразование (вращение) системы координат
, а линии равного уровня имеют ось симметрии, например, на рис. 57.1 линии – это эллипсы, тогда можно выполнить преобразование (вращение) системы координат 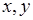 , такое, что в новой системе ковариация
, такое, что в новой системе ковариация 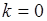 . Это означает также и преобразование случайных величин
. Это означает также и преобразование случайных величин 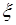 ,
,  с ненулевой ковариацией к новым случайным величинам, для которых ковариация равна нулю.
с ненулевой ковариацией к новым случайным величинам, для которых ковариация равна нулю.
|
|
Коэффициент корреляции
58.1. Коэффициентом корреляции двух случайных величин 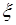 и
и 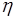 называется число
называется число
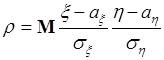 . (58.1)
. (58.1)
Коэффициент корреляции является ковариацией: 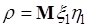 двух безразмерных случайных величин
двух безразмерных случайных величин
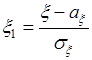 ,
, 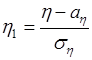 , (58.2)
, (58.2)
полученных из исходных величин 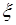 и
и  путем преобразования специального вида (58.2) (нормировки), которое обеспечивает нулевые средние
путем преобразования специального вида (58.2) (нормировки), которое обеспечивает нулевые средние 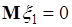 ,
,  и единичные дисперсии
и единичные дисперсии 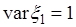 ,
, 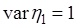 .
.
Коэффициент корреляции (58.1) можно представить через ковариацию 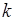 случайных величин
случайных величин 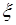 и
и  :
:
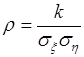 . (58.3)
. (58.3)
Поскольку 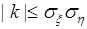 , то из (58.3) следует
, то из (58.3) следует
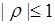 . (58.4)
. (58.4)
Коэффициент корреляции является безразмерной величиной, принимает значения на интервале 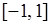 и поэтому используется как мера статистической связи линейного типа между случайными величинами
и поэтому используется как мера статистической связи линейного типа между случайными величинами 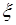 и
и  , в отличие от ковариации
, в отличие от ковариации 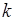 , для которой интервал значений
, для которой интервал значений 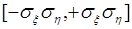 зависит от дисперсий случайных величин. Рассмотрим примеры вычисления коэффициента корреляции, позволяющие выяснить свойства
зависит от дисперсий случайных величин. Рассмотрим примеры вычисления коэффициента корреляции, позволяющие выяснить свойства  как меры статистической связи между случайными величинами.
как меры статистической связи между случайными величинами.
58.2. Пусть 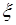 - случайная величина с математическим ожиданием
- случайная величина с математическим ожиданием 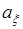 , дисперсией
, дисперсией 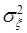 и
и 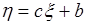 . Ковариация случайных величин
. Ковариация случайных величин 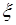 и
и 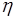 определяется формулой (56.5):
определяется формулой (56.5): 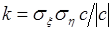 . Подставим это соотношение в (58.3), тогда:
. Подставим это соотношение в (58.3), тогда:
 (58.4)
(58.4)
Таким образом, для случайных величин 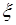 ,
, 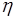 , связанных линейной зависимостью коэффициент корреляции
, связанных линейной зависимостью коэффициент корреляции  принимает либо максимальное значение
принимает либо максимальное значение 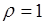 , либо минимальное -
, либо минимальное - 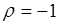 .
.
58.3. Рассмотрим обобщение линейной функции, связывающей случайные величины 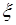 и
и  на линейную случайную функцию следующего вида:
на линейную случайную функцию следующего вида:
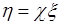 (58.5)
(58.5)
где 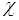 и
и 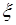 - независимые случайные величины. В частном случае
- независимые случайные величины. В частном случае 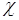 - число и (58.5) – линейная функция, определяющая
- число и (58.5) – линейная функция, определяющая  через
через 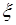 . Для детерминированной линейной связи
. Для детерминированной линейной связи 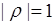 - принимает максимальное значение. Если
- принимает максимальное значение. Если 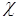 - случайная величина, то связь (58.5) становится статистической (стохастической, случайной), то есть не столь жесткой как детерминированная функциональная связь. Это приводит к
- случайная величина, то связь (58.5) становится статистической (стохастической, случайной), то есть не столь жесткой как детерминированная функциональная связь. Это приводит к  . В зависимости от свойств случайной величины
. В зависимости от свойств случайной величины 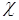 статистическая связь между
статистическая связь между 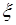 и
и  может быть сильной,
может быть сильной,  , или слабой,
, или слабой, 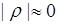 . Для того, чтобы ответить на вопрос, какова мера связи между случайными величинами
. Для того, чтобы ответить на вопрос, какова мера связи между случайными величинами 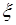 и
и 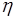 (58.5) вычислим их коэффициент корреляции.
(58.5) вычислим их коэффициент корреляции.
|
|
Пусть 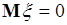 ,
,  ,
, 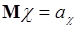 ,
, 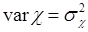 . Тогда из (58.5) следует, в силу независимости
. Тогда из (58.5) следует, в силу независимости 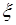 и
и 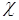 :
:
 .
.
Выразим дисперсию случайные величины  через параметры случайных величин
через параметры случайных величин 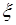 ,
,  :
:
 . (58.6)
. (58.6)
Теперь по формуле (58.3):
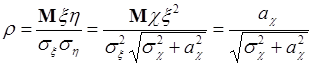 . (58.7)
. (58.7)
Если 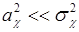 , то из (58.7) следует
, то из (58.7) следует 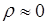 , что соответствует слабой связи между случайными величинами
, что соответствует слабой связи между случайными величинами 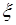 и
и  . Если
. Если 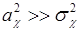 , из (58.7) следует
, из (58.7) следует 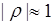 , связь становится сильной и в пределе при
, связь становится сильной и в пределе при 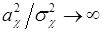 переходит в детерминированную линейную связь.
переходит в детерминированную линейную связь.
|
|
|

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!