Расчет ККЭ – очень сложная математическая задача, включающая проблему неоднородных двумерных граничных условий. Чтобы упростить проблему граничных условий до выполнимого уровня, мы сделаем несколько предположений. Упрощенная геометрия короткоканального МОПТ представлена на рис.С1.5. Область определения – прямоугольный бокс с длиной, равной длине канала L, определяемой как расстояние между истоком и стоком (рис.С1.5). В вертикальном направлении бокс состоит из области оксида, толщиной 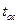 , и области кремния, определяемой толщиной обедненного слоя
, и области кремния, определяемой толщиной обедненного слоя 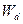 .
.
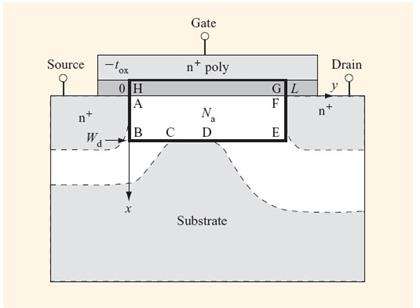
Рис. С1.5 Упрощенная геометрия для аналитического решения уравнения Пуассона в короткоканальном МОПТ. Затемненные площади в подложке представляют собой проводящие области постоянного потенциала [4].
Ось х направлена вертикально вниз, ось у – горизонтально, начало координат в точке А. Потенциал 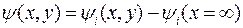 определяется как потенциал в точке (х,у) относительно потенциала р -подложки. Подложка предполагается равномерно легированной с концентрацией Na. В области окисла AFGH уравнение Пуассона переходит в уравнение Лапласа (заряды отсутствуют):
определяется как потенциал в точке (х,у) относительно потенциала р -подложки. Подложка предполагается равномерно легированной с концентрацией Na. В области окисла AFGH уравнение Пуассона переходит в уравнение Лапласа (заряды отсутствуют):
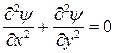 . (С1.3)
. (С1.3)
В подпороговой области (до порога включительно) концентрация подвижных носителей в обедненной области кремния (и дырок, и электронов) предполагается пренебрежимо малой. Поэтому уравнение Пуассона имеет вид
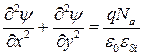 . (С1.4)
. (С1.4)
Длина области кремния равна длине канала L. Глубина обедненного слоя,  , будет определена позднее.
, будет определена позднее.
Как следует из условия 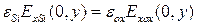 (закон Гаусса), нормальная компонента электрического поля
(закон Гаусса), нормальная компонента электрического поля 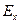 изменяется с коэффициентом
изменяется с коэффициентом 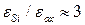 при переходе через границу кремний-окисел AF (скачок электрического поля). Чтобы исключить это граничное условие так, чтобы
при переходе через границу кремний-окисел AF (скачок электрического поля). Чтобы исключить это граничное условие так, чтобы 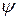 и его производные были непрерывны (отсутствует скачок потенциала), окисел заменяется некоторой эквивалентной областью с той же самой диэлектрической постоянной, что и у кремния, но с толщиной, равной
и его производные были непрерывны (отсутствует скачок потенциала), окисел заменяется некоторой эквивалентной областью с той же самой диэлектрической постоянной, что и у кремния, но с толщиной, равной  . Это сохраняет величину подзатворной емкости и позволяет рассматривать прямоугольную область как гомогенный (однородный) материал с высотой
. Это сохраняет величину подзатворной емкости и позволяет рассматривать прямоугольную область как гомогенный (однородный) материал с высотой 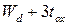 и диэлектрической постоянной
и диэлектрической постоянной 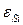 . Это является хорошим предположением, когда оксид тонок по сравнению с толщиной обедненной области
. Это является хорошим предположением, когда оксид тонок по сравнению с толщиной обедненной области 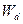 , как это имеет место в большинстве реальных технологий. Недостатком такого подхода может быть некоторая ошибка в тангенциальной (по оси у) компоненте поля, величина которой не изменяется на границе окисел-кремний. Ошибка ожидается малой, когда толщина подзатворного окисла значительно меньше толщины обедненной области
, как это имеет место в большинстве реальных технологий. Недостатком такого подхода может быть некоторая ошибка в тангенциальной (по оси у) компоненте поля, величина которой не изменяется на границе окисел-кремний. Ошибка ожидается малой, когда толщина подзатворного окисла значительно меньше толщины обедненной области  , так что в окисле доминирует нормальная компонента.
, так что в окисле доминирует нормальная компонента.
Если мы предполагаем, что переходы стока и истока резкие и глубже, чем  [1], мы можем записать следующий набор упрощенных граничных условий:
[1], мы можем записать следующий набор упрощенных граничных условий:
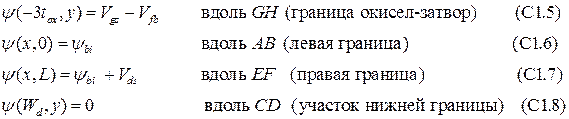
где 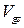 и
и 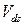 − напряжения на затворе и стоке,
− напряжения на затворе и стоке, 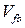 − напряжение плоских зон, и
− напряжение плоских зон, и 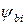 − контактная разность потенциалов переходов стока и истока. Для резкого п +- р перехода
− контактная разность потенциалов переходов стока и истока. Для резкого п +- р перехода 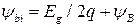 . Типично
. Типично 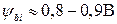 . Если имеется смещение подложки
. Если имеется смещение подложки 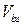 , то
, то 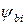 заменяется на
заменяется на 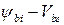 в выражениях (С1.6) и (С1.7) и
в выражениях (С1.6) и (С1.7) и 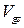 − на
− на 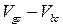 в выражении (С1.5). Нижняя граница фактически подвижна, так как
в выражении (С1.5). Нижняя граница фактически подвижна, так как  изменяется с изменением напряжения
изменяется с изменением напряжения 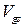 . Расстояние ВС приблизительно определяется толщиной ОПЗ перехода истока
. Расстояние ВС приблизительно определяется толщиной ОПЗ перехода истока
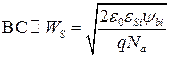 . (С1.9)
. (С1.9)
Подобным же образом расстояние DE определяется толщиной ОПЗ перехода стока
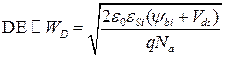 . (С1.10)
. (С1.10)
Граничные условия для потенциала вдоль FG и HA (то есть в окисле) предполагают линейное изменение между значениями в конечных точках, в то время как вдоль BC и DE предполагается параболическое изменение между конечными точками.
С1.5 Метод решения
Метод решения использует принцип суперпозиции и заключается в представлении электростатического потенциала в виде следующих слагаемых:
 . (С1.11)
. (С1.11)
Здесь  − решение неоднородного уравнения (Пуассона), удовлетворяющее верхнему граничному условию (С1.5).
− решение неоднородного уравнения (Пуассона), удовлетворяющее верхнему граничному условию (С1.5).  ,
,  ,
, 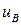 − решения однородного уравнении (Лапласа), выбранные надлежащим образом для удовлетворения остальным граничным условиям, а именно, на левой, правой и нижней стороне прямоугольного бокса на рис.С1.4. Например,
− решения однородного уравнении (Лапласа), выбранные надлежащим образом для удовлетворения остальным граничным условиям, а именно, на левой, правой и нижней стороне прямоугольного бокса на рис.С1.4. Например,  равно нулю на верхней, нижней и правой границах, но
равно нулю на верхней, нижней и правой границах, но  удовлетворяет левому граничному условию (С1.6). Подобным же образом,
удовлетворяет левому граничному условию (С1.6). Подобным же образом,  равно нулю на верхней, нижней и левой границах, но
равно нулю на верхней, нижней и левой границах, но  удовлетворяет правому граничному условию (С1.7) и т.д.
удовлетворяет правому граничному условию (С1.7) и т.д.
Естественным выбором для  [фактически
[фактически  ] является решение для одномерного МОПТ, использующее приближение полного обеднения:
] является решение для одномерного МОПТ, использующее приближение полного обеднения:
 для области окисла
для области окисла  , (С1.12)
, (С1.12)
и  для области кремния
для области кремния  . (С1.13)
. (С1.13)
Здесь  − длинноканальный поверхностный потенциал, который изменяется с напряжением
− длинноканальный поверхностный потенциал, который изменяется с напряжением  . Он связан с толщиной ОПЗ
. Он связан с толщиной ОПЗ  формулой
формулой
 , (С1.14)
, (С1.14)
чтобы удовлетворять выражению (С1.4). Заметим, что выражения (С1.12) и (С1.13) удовлетворяют верхнему и части CD нижнего граничных условий, [выражения (С1.5) и (С1.8)], и непрерывны при х = 0. Требование, чтобы  было непрерывно при х = 0, позволяет найти соотношение между
было непрерывно при х = 0, позволяет найти соотношение между  и
и  :
:
 , (С1.15)
, (С1.15)
где  определяется выражением (С1.14). Заметим, что выражение (С1.15) совпадает с выражением для смещения затвора в подпороговой области:
определяется выражением (С1.14). Заметим, что выражение (С1.15) совпадает с выражением для смещения затвора в подпороговой области:  .
.
Остальные слагаемые решения в (С1.11) имеют следующую форму
 , (С1.16)
, (С1.16)
 , (С1.17)
, (С1.17)
 . (С1.18)
. (С1.18)
Коэффициенты определяются из требования удовлетворения  граничным условиям. Например, на левой границе
граничным условиям. Например, на левой границе
 . (С1.19)
. (С1.19)
Для вычисления отдельных коэффициентов  выражение (С1.19) умножается на ортогональные собственные функции и интегрируется от −
выражение (С1.19) умножается на ортогональные собственные функции и интегрируется от −  до
до  :
:
 . (С1.20)
. (С1.20)
 определяется выражениями (С1.12) и (С1.13). Но граничное условие (С1.6) точно определяет
определяется выражениями (С1.12) и (С1.13). Но граничное условие (С1.6) точно определяет  только на отрезке
только на отрезке  . Чтобы дополнить значения
. Чтобы дополнить значения  для неустановленного точно промежутка вдоль отрезка НА на рис.С1.4, используется линейная интерполяция между значениями
для неустановленного точно промежутка вдоль отрезка НА на рис.С1.4, используется линейная интерполяция между значениями 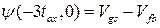 и
и 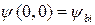 для отрезка
для отрезка 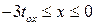 . Это хорошая аппроксимация, если ширина зазора
. Это хорошая аппроксимация, если ширина зазора  много меньше, чем
много меньше, чем  .
.
В середине прибора,  , члены в
, члены в  и
и 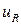 изменяются как
изменяются как  . Если длина канала L не слишком короткая, членами высокого порядка в обоих рядах можно пренебречь. Выполняя интегрирование в (С1.20) для n =1, получаем
. Если длина канала L не слишком короткая, членами высокого порядка в обоих рядах можно пренебречь. Выполняя интегрирование в (С1.20) для n =1, получаем
 , (С1.21)
, (С1.21)
где  . Так как
. Так как  мало по сравнению с
мало по сравнению с  , хорошей аппроксимацией является
, хорошей аппроксимацией является  , так что
, так что
 , (С1.22)
, (С1.22)
где  для 15°
для 15°  45°. Подобным же образом коэффициент наименьшего порядка в ряду
45°. Подобным же образом коэффициент наименьшего порядка в ряду  получается из правого граничного условия
получается из правого граничного условия
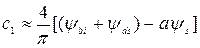 . (С1.23)
. (С1.23)
Третьим рядом,  , можно полностью пренебречь, так как граничное условие, выражение (С1.8), на большей части нижнего граничного условия (С D на рис. С1.4) уже удовлетворяет
, можно полностью пренебречь, так как граничное условие, выражение (С1.8), на большей части нижнего граничного условия (С D на рис. С1.4) уже удовлетворяет  , следовательно, и
, следовательно, и  . Остающийся вклад в коэффициент
. Остающийся вклад в коэффициент  от сегментов ВС и DE много меньше, чем
от сегментов ВС и DE много меньше, чем  или
или  .
.
Приближенное аналитическое решение для области кремния  в подпороговой области тогда
в подпороговой области тогда
 .(С1.24)
.(С1.24)
Вычисление поля  из вышеприведенного выражения показывает, что оно ведет себя так, как представлено на рис. С1.4(а) и (b). Характеристическая длина экспоненциального спада равна
из вышеприведенного выражения показывает, что оно ведет себя так, как представлено на рис. С1.4(а) и (b). Характеристическая длина экспоненциального спада равна 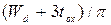 , и она масштабируется вместе с вертикальным размером прямоугольной области на рис. С1.4.
, и она масштабируется вместе с вертикальным размером прямоугольной области на рис. С1.4.



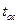 , и области кремния, определяемой толщиной обедненного слоя
, и области кремния, определяемой толщиной обедненного слоя 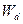 .
.
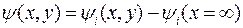 определяется как потенциал в точке (х,у) относительно потенциала р -подложки. Подложка предполагается равномерно легированной с концентрацией Na. В области окисла AFGH уравнение Пуассона переходит в уравнение Лапласа (заряды отсутствуют):
определяется как потенциал в точке (х,у) относительно потенциала р -подложки. Подложка предполагается равномерно легированной с концентрацией Na. В области окисла AFGH уравнение Пуассона переходит в уравнение Лапласа (заряды отсутствуют):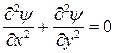 . (С1.3)
. (С1.3)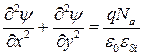 . (С1.4)
. (С1.4) , будет определена позднее.
, будет определена позднее.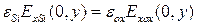 (закон Гаусса), нормальная компонента электрического поля
(закон Гаусса), нормальная компонента электрического поля 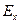 изменяется с коэффициентом
изменяется с коэффициентом 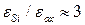 при переходе через границу кремний-окисел AF (скачок электрического поля). Чтобы исключить это граничное условие так, чтобы
при переходе через границу кремний-окисел AF (скачок электрического поля). Чтобы исключить это граничное условие так, чтобы 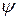 и его производные были непрерывны (отсутствует скачок потенциала), окисел заменяется некоторой эквивалентной областью с той же самой диэлектрической постоянной, что и у кремния, но с толщиной, равной
и его производные были непрерывны (отсутствует скачок потенциала), окисел заменяется некоторой эквивалентной областью с той же самой диэлектрической постоянной, что и у кремния, но с толщиной, равной  . Это сохраняет величину подзатворной емкости и позволяет рассматривать прямоугольную область как гомогенный (однородный) материал с высотой
. Это сохраняет величину подзатворной емкости и позволяет рассматривать прямоугольную область как гомогенный (однородный) материал с высотой 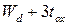 и диэлектрической постоянной
и диэлектрической постоянной 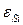 . Это является хорошим предположением, когда оксид тонок по сравнению с толщиной обедненной области
. Это является хорошим предположением, когда оксид тонок по сравнению с толщиной обедненной области  , так что в окисле доминирует нормальная компонента.
, так что в окисле доминирует нормальная компонента.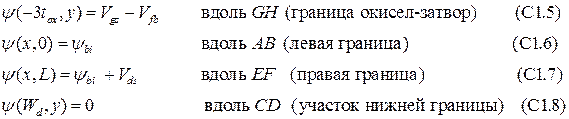
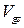 и
и 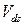 − напряжения на затворе и стоке,
− напряжения на затворе и стоке, 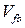 − напряжение плоских зон, и
− напряжение плоских зон, и 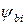 − контактная разность потенциалов переходов стока и истока. Для резкого п +- р перехода
− контактная разность потенциалов переходов стока и истока. Для резкого п +- р перехода 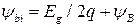 . Типично
. Типично 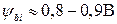 . Если имеется смещение подложки
. Если имеется смещение подложки 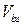 , то
, то 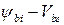 в выражениях (С1.6) и (С1.7) и
в выражениях (С1.6) и (С1.7) и 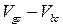 в выражении (С1.5). Нижняя граница фактически подвижна, так как
в выражении (С1.5). Нижняя граница фактически подвижна, так как 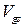 . Расстояние ВС приблизительно определяется толщиной ОПЗ перехода истока
. Расстояние ВС приблизительно определяется толщиной ОПЗ перехода истока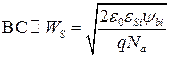 . (С1.9)
. (С1.9)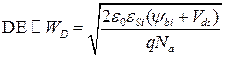 . (С1.10)
. (С1.10) . (С1.11)
. (С1.11) − решение неоднородного уравнения (Пуассона), удовлетворяющее верхнему граничному условию (С1.5).
− решение неоднородного уравнения (Пуассона), удовлетворяющее верхнему граничному условию (С1.5).  ,
,  ,
, 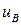 − решения однородного уравнении (Лапласа), выбранные надлежащим образом для удовлетворения остальным граничным условиям, а именно, на левой, правой и нижней стороне прямоугольного бокса на рис.С1.4. Например,
− решения однородного уравнении (Лапласа), выбранные надлежащим образом для удовлетворения остальным граничным условиям, а именно, на левой, правой и нижней стороне прямоугольного бокса на рис.С1.4. Например,  равно нулю на верхней, нижней и правой границах, но
равно нулю на верхней, нижней и правой границах, но  удовлетворяет левому граничному условию (С1.6). Подобным же образом,
удовлетворяет левому граничному условию (С1.6). Подобным же образом,  удовлетворяет правому граничному условию (С1.7) и т.д.
удовлетворяет правому граничному условию (С1.7) и т.д. ] является решение для одномерного МОПТ, использующее приближение полного обеднения:
] является решение для одномерного МОПТ, использующее приближение полного обеднения: для области окисла
для области окисла  , (С1.12)
, (С1.12) для области кремния
для области кремния  . (С1.13)
. (С1.13) − длинноканальный поверхностный потенциал, который изменяется с напряжением
− длинноканальный поверхностный потенциал, который изменяется с напряжением  . Он связан с толщиной ОПЗ
. Он связан с толщиной ОПЗ  формулой
формулой , (С1.14)
, (С1.14) было непрерывно при х = 0, позволяет найти соотношение между
было непрерывно при х = 0, позволяет найти соотношение между  , (С1.15)
, (С1.15) .
. , (С1.16)
, (С1.16) , (С1.17)
, (С1.17) . (С1.18)
. (С1.18) граничным условиям. Например, на левой границе
граничным условиям. Например, на левой границе . (С1.19)
. (С1.19) выражение (С1.19) умножается на ортогональные собственные функции и интегрируется от −
выражение (С1.19) умножается на ортогональные собственные функции и интегрируется от −  до
до  :
: . (С1.20)
. (С1.20) определяется выражениями (С1.12) и (С1.13). Но граничное условие (С1.6) точно определяет
определяется выражениями (С1.12) и (С1.13). Но граничное условие (С1.6) точно определяет  только на отрезке
только на отрезке  для неустановленного точно промежутка вдоль отрезка НА на рис.С1.4, используется линейная интерполяция между значениями
для неустановленного точно промежутка вдоль отрезка НА на рис.С1.4, используется линейная интерполяция между значениями 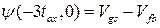 и
и 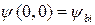 для отрезка
для отрезка 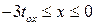 . Это хорошая аппроксимация, если ширина зазора
. Это хорошая аппроксимация, если ширина зазора  , члены в
, члены в  и
и 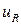 изменяются как
изменяются как  . Если длина канала L не слишком короткая, членами высокого порядка в обоих рядах можно пренебречь. Выполняя интегрирование в (С1.20) для n =1, получаем
. Если длина канала L не слишком короткая, членами высокого порядка в обоих рядах можно пренебречь. Выполняя интегрирование в (С1.20) для n =1, получаем , (С1.21)
, (С1.21) . Так как
. Так как  мало по сравнению с
мало по сравнению с  , хорошей аппроксимацией является
, хорошей аппроксимацией является  , так что
, так что , (С1.22)
, (С1.22) для 15°
для 15°  45°. Подобным же образом коэффициент наименьшего порядка в ряду
45°. Подобным же образом коэффициент наименьшего порядка в ряду  получается из правого граничного условия
получается из правого граничного условия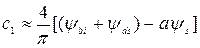 . (С1.23)
. (С1.23) , можно полностью пренебречь, так как граничное условие, выражение (С1.8), на большей части нижнего граничного условия (С D на рис. С1.4) уже удовлетворяет
, можно полностью пренебречь, так как граничное условие, выражение (С1.8), на большей части нижнего граничного условия (С D на рис. С1.4) уже удовлетворяет  , следовательно, и
, следовательно, и  . Остающийся вклад в коэффициент
. Остающийся вклад в коэффициент  от сегментов ВС и DE много меньше, чем
от сегментов ВС и DE много меньше, чем  или
или  .
. в подпороговой области тогда
в подпороговой области тогда .(С1.24)
.(С1.24) из вышеприведенного выражения показывает, что оно ведет себя так, как представлено на рис. С1.4(а) и (b). Характеристическая длина экспоненциального спада равна
из вышеприведенного выражения показывает, что оно ведет себя так, как представлено на рис. С1.4(а) и (b). Характеристическая длина экспоненциального спада равна 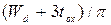 , и она масштабируется вместе с вертикальным размером прямоугольной области на рис. С1.4.
, и она масштабируется вместе с вертикальным размером прямоугольной области на рис. С1.4.


