Требуется найти функцию Y = Y (х), удовлетворяющую уравнению
dY / dx = f (x, Y) (7.2)
и принимающую при x = x 0 заданное значение Y 0:
Y (x 0) = Y 0. (7.3)
При этом будем для определённости считать, что решение нужно получить для значений x > x 0.
Из курса дифференциальных уравнений известно, что решение Y (x) задачи (7.2), (7.3) существует, единственно и является гладкой функцией, если правая часть f (x, Y)уравнения (7.2), являющаяся функцией двух переменных х, Y,удовлетворяет некоторым условиям гладкости [20]. Будем считать, что эти условия выполнены и существует единственное гладкое решение Y (x).
Простейшим численным методом решения задачи Коши для
обыкновенного дифференциального уравнения является метод Эйлера [7]. Он основан на разложении искомой функции Y (х)в ряд Тейлора в окрестностях узлов х = xi (i = 0, 1, …), в котором отбрасываются все члены, содержащие производные второго и более высоких порядков. Запишем это разложение в виде
Y (xi + ∆ xi)= Y (xi) + Y ' (xi)∙∆ xi. (7.4)
Заменяем значения функции Y в узлах xi значениями сеточной функции yi. Кроме того, используя уравнение (7.2), полагаем
Y ' (xi) = f (xi, Y (xi)) = f (xi, yi).
Будем считать для простоты узлы равноотстоящими, т. е. ∆ xi = xi + 1- xi = h = = const (i = 0, 1,...). Учитывая введенные обозначения,из равенства (7.4) получаем
yi+ 1 = yi + h ∙ f (xi, yi), i = 0, 1, … (7.5)
Полагая i = 0, с помощью соотношения (7.5) находим значение сеточной функции y 1при х = x 1:
y 1 = y 0 + h ∙ f (x 0, y 0).
Требуемое здесь значение у 0задано начальным условием (7.3), т. е. у 0 = Y (x 0) = = Y 0. Аналогично могут быть найдены значения сеточной функции в других узлах:
y 2 = y 1 + h ∙ f (x 1, y 1),
………………………
yn = yn - 1 + h ∙ f (x n - 1, y n - 1).
Построенный алгоритм называется методом Эйлера. Разностная схема этого метода представлена соотношениями (7.5). Они имеют вид рекуррентных формул, с помощью которых значение сеточной функции yi + 1 в любом узле xi + 1вычисляется по ее значению yi в предыдущем узле xi. В связи с этим метод Эйлера относится к одношаговым методам.
Блок-схема алгоритма решения задачи Коши (7.2), (7.3) методом Эйлера изображена на рис. 7.1. Задаются начальные значения х, у 0,а также величина
шага h и количество расчетных точек n. Решение получается в узлах х + h, х +
+2 h, …, х + nh. Вывод результатов предусмотрен на каждом шаге.
На рис. 7.2. дана геометрическая интерпретация метода Эйлера. Изображены первые два шага, т. е. проиллюстрировано вычисление сеточной функции в точках х 1, х 2. Интегральные кривые 0, 1, 2 описывают точные решения уравнения (7.2). При этом кривая 0 соответствует точному решению задачи Коши (7.2), (7.3), так как она проходит через начальную точку А (х 0, y 0). Точки В, С получены в результате численного решения задачи Коши методом Эйлера. Их отклонения от кривой 0 характеризуют погрешность метода. При выполнении каждого шага мы фактически попадаем на другую интегральную кривую. Отрезок АВ – отрезок касательной к кривой 0 в точке А, ее наклон характеризуется значением производной y 0 = f (x 0, y 0).Касательная ВС уже проводится к другой
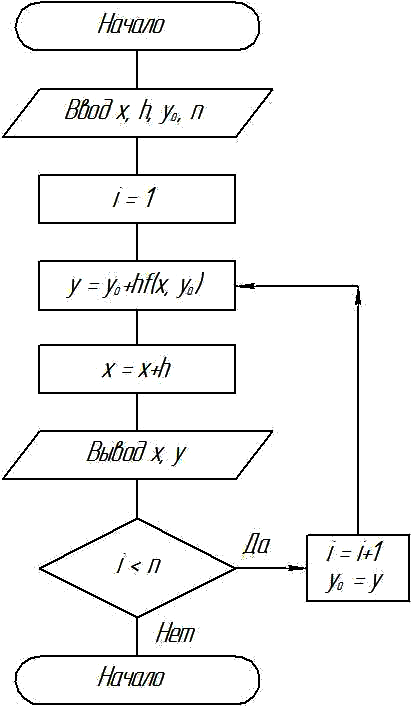
Рис. 7.1. Блок-схема метода Эйлера
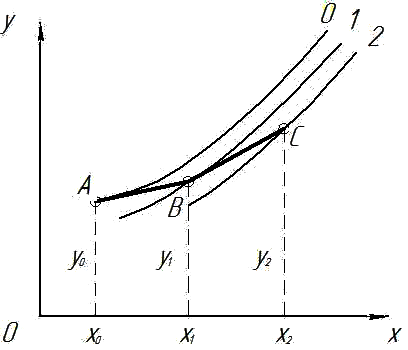
Рис. 7.2. Иллюстрация метода Эйлера
интегральной кривой 1.Таким образом, погрешность метода Эйлера приводит к тому, что на каждом шаге решение переходит на другую интегральную кривую.
Метод Эйлера имеет первый порядок точности [8, 18], т.е. погрешность метода достаточно высока.
Метод Рунге-Кутта. Пример решения дифференциального уравнения
Наиболее распространенным явным одношаговым методом решения задачи Коши является метод Рунге – Кутта [7]. На его основе могут быть построены разностные схемы разного порядка точности. Приведем схему Рунге – Кутта четвертого порядка. Алгоритм этого метода имеет следующий вид:
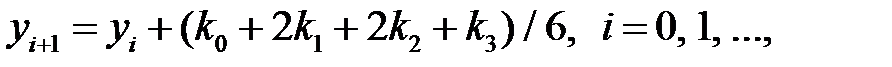
 (7.6)
(7.6)
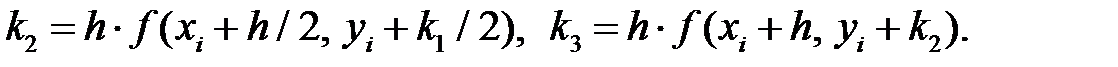
Из формул (7.6) следует, что метод Рунге – Кутта требует на каждом шаге четырехкратного вычисления правой части уравнения f (x, у).
Метод Эйлера (7.5) может рассматриваться как метод Рунге – Кутта первого порядка точности. Метод Рунге – Кутта (7.6) требует большего объема вычислений, однако это окупается повышенной точностью, что дает возможность проводить расчеты с большим шагом. Другими словами, для получения результатов с одинаковой точностью в методе Эйлера потребуется значительно меньший шаг, чем в методе Рунге – Кутта.
Проведем сравнительную оценку рассмотренных методов на простом примере, позволяющем получить также и точное решение.
Пример. Решить задачу Коши
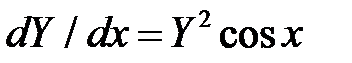 , Y (0) = 1, 0
, Y (0) = 1, 0  x
x  1, h = 0,1.
1, h = 0,1.
Сформулированная задача может быть решена известными из курса высшей математики методами. Опустив выкладки, запишем окончательное выражение для точного решения с учетом заданного начального условия. Оно имеет вид
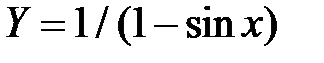 .
.
Проведем теперь решение данной задачи численно с помощью рассмотренных выше методов. Расчет для двух точек (i = 1 и i = 2) по формуле Эйлера (7.5):
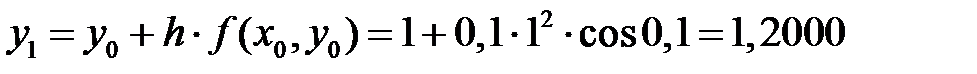 ;
;
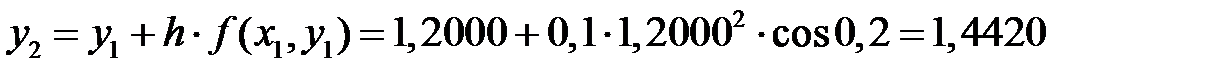 .
.
Расчет для двух точек (i = 1 и i = 2) по формулам Рунге – Кутта (7.6):
i = 1; 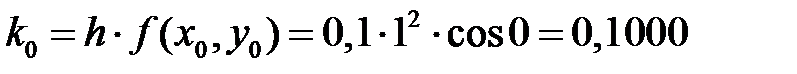 ;
;
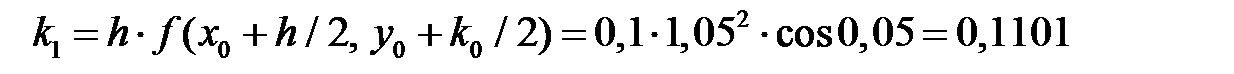 ;
;
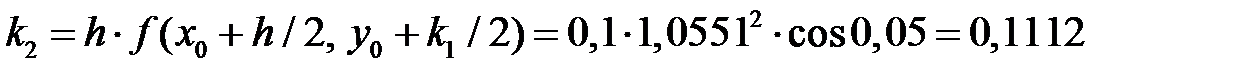 ;
;
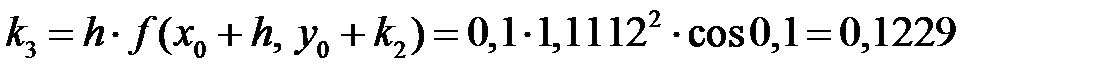 ;
;
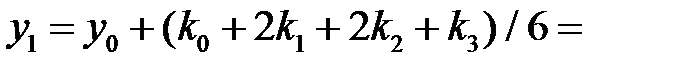
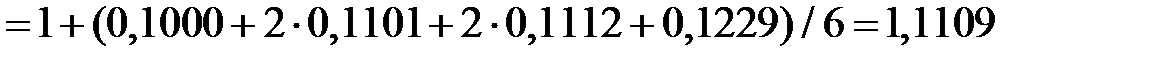 ;
;
i = 2; 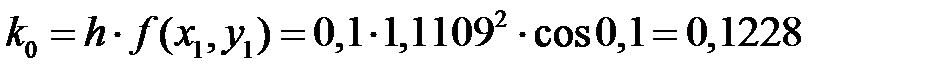 ;
;
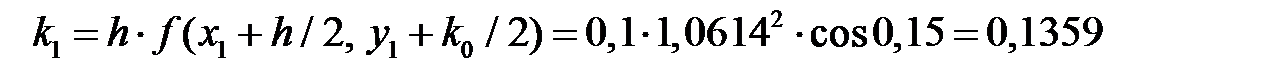 ;
;
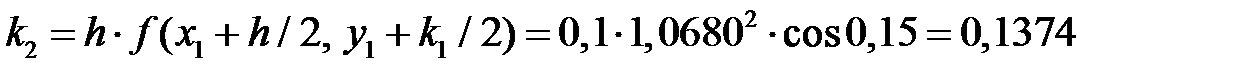 ;
;
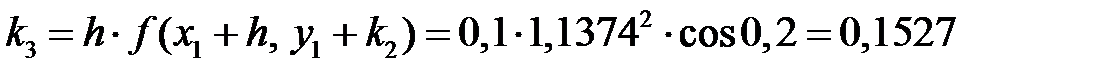 ;
;

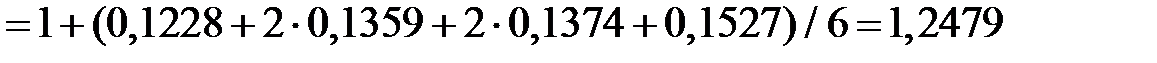 .
.
Результаты всех вычислений приведены в табл. 7.1. Как видно из этой таблицы, более точным является решение, полученное методом Рунге – Кутта. Анализ решения с использованием метода Эйлера позволяет проследить рост погрешности с возрастанием х i. При х i = 1 погрешность составляет 35%.
Таблица 7.1
Результаты численного решения задачи Коши
| i
| х i
| у i
|
| Метод
Эйлера
| Метод
Рунге-Кутта
| Точное
решение
|
| 0
| 0,0
| 1,000
| 1,000
| 1,000
|
| 1
| 0,1
| 1,1000
| 1,1109
| 1,1109
|
| 2
| 0,2
| 1,2204
| 1,2479
| 1,2479
|
| 3
| 0,3
| 1,3664
| 1,4195
| 1,4195
|
| 4
| 0,4
| 1,5447
| 1,6378
| 1,6378
|
| 5
| 0,5
| 1,7645
| 1,9209
| 1,9210
|
| 6
| 0,6
| 2,0377
| 2,2969
| 2,2970
|
| 7
| 0,7
| 2,3804
| 2,8106
| 2,8107
|
| 8
| 0,8
| 2,8138
| 3,5377
| 3,5380
|
| 9
| 0,9
| 3,3655
| 4,6144
| 4,6152
|
| 10
| 1,0
| 4,0695
| 6,3056
| 6,3080
|
С уменьшением шага h локальная погрешность метода Эйлера снизится. Если в рассматриваемом примере принять h = 0,05, то при х i = 1 погрешность составляет уже 24% (у i = 4,7897). Однако при уменьшении h возрастет число узлов, что приводит к увеличению объема вычислений. Поэтому метод Эйлера
применяется сравнительно редко. Наиболее употребительным одношаговым методом является метод Рунге – Кутта.





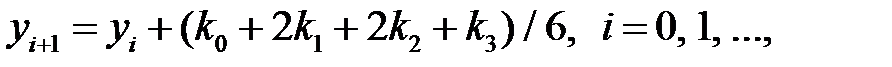
 (7.6)
(7.6)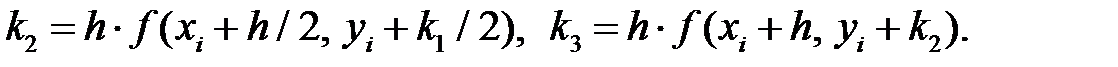
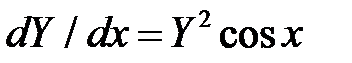 , Y (0) = 1, 0
, Y (0) = 1, 0 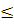 x
x 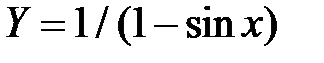 .
.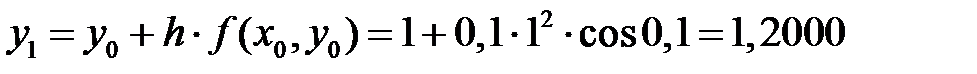 ;
;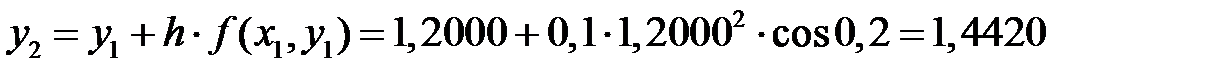 .
.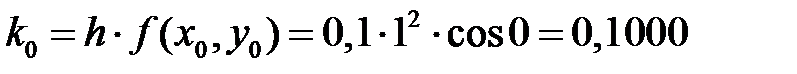 ;
;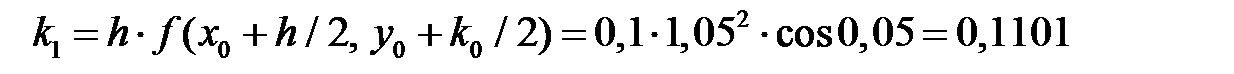 ;
;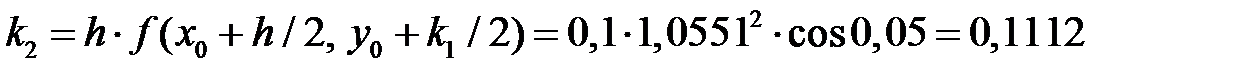 ;
;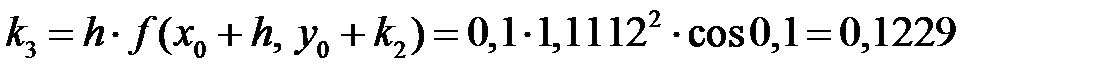 ;
;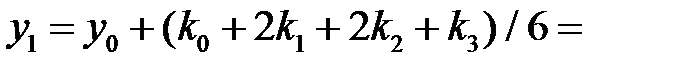
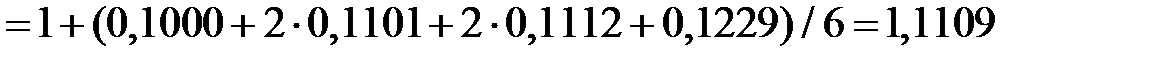 ;
;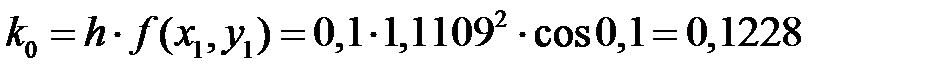 ;
;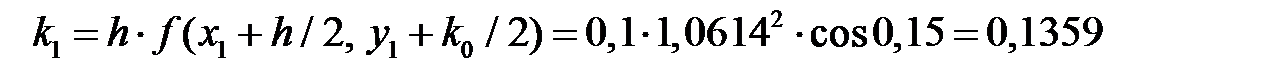 ;
;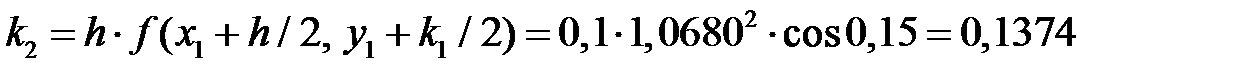 ;
;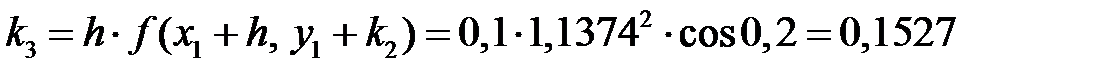 ;
;
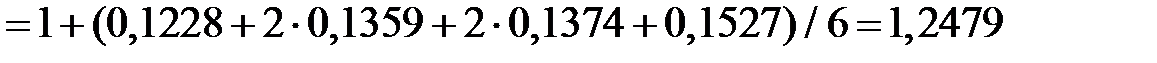 .
.


