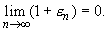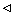Когда данные сортируются не в оперативной памяти, а на жестком диске, особенно если ключ связан с большим объемом дополнительной информации, то количество перемещений элементов существенно влияет на время работы. Этот алгоритм уменьшает количество таких перемещений, действуя следующим образом: за один проход из всех элементов выбираются минимальный и максимальный. Потом минимальный элемент помещается в начало массива, а максимальный, соответственно, в конец. Далее алгоритм выполняется для остальных данных. Таким образом, за каждый проход два элемента помещаются на свои места, а значит, понадобится N/2 проходов, где N - количество элементов. Реализацияданного алгоритма выглядит так:
Program ShakerSort;
Var A: array[1..1000] of integer;
N,i,j,p: integer;
Min, Max: integer;
Begin
{Определение размера массива A - N) и его заполнение}
…
{ сортировка данных }
for i:=1 to n div 2 do
begin
if A[i]>A[i+1] then
begin
Min:=i+1;
Max:=i;
end
else
begin
Min:=i;
Max:=i+1;
end;
for j:=i+2 to n-i+1 do
if A[j]>A[Max] then
Max:=j
else
if A[j]<A[Min] then
Min:=j;
{ Обмен элементов }
P:=A[i];
A[i]:=A[min];
A[min]:=P;
if max=i then
max:=min;
P:=A[N-i+1];
A[N-i+1]:=A[max];
A[max]:=P;
end;
{Вывод отсортированного массива A}
…
End.
Рассмотрев эти методы, сделаем определенные выводы. Их объединяет не только то, что они сортируют данные, но также и время их работы. В каждом из алгоритмов присутствуют вложенные циклы, время выполнения которых зависит от размера входных данных. Значит, общее время выполнения программ есть O(n2) (константа, умноженная на n2). Следует отметить, что первые два алгоритма используют также O(n2) перестановок, в то время как третий использует их O(n). Отсюда следует, что метод Шейкера является более выгодным для сортировки данных на внешних носителях информации.
Алгоритм 4. Сортировка слиянием.
Эта сортировка использует следующую подзадачу: есть два отсортированных массива, нужно сделать (слить) из них один отсортированный. Алгоритм сортировки работает по такому принципу: разбивается массив на две части, отсортировывается каждая из них, а потом сливаются обе части в одну отсортированную. Корректность данного метода практически очевидна, поэтому перейдем к реализации.
Program SlivSort;
Var A,B: array[1..1000] of integer;
N: integer;
Procedure Sliv(p,q: integer); { процедура сливающая массивы }
Var r,i,j,k: integer;
Begin
r:=(p+q) div 2;
i:=p;
j:=r+1;
for k:=p to q do
if (i<=r) and ((j>q) or (a[i]<a[j])) then
begin
b[k]:=a[i];
i:=i+1;
end
else
begin
b[k]:=a[j];
j:=j+1;
end;
for k:=p to q do
a[k]:=b[k];
End;
Procedure Sort(p,q: integer); {p,q - индексы начала и конца сортируемой части массива }
Begin
if p<q then {массив из одного элемента тривиально упорядочен}
begin
Sort(p,(p+q) div 2);
Sort((p+q) div 2 + 1,q);
Sliv(p,q);
end;
End;
Begin
{Определение размера массива A - N) и его заполнение}
…
{запуск сортирующей процедуры}
Sort(1,N);
{Вывод отсортированного массива A}
…
End.
Чтобы оценить время работы этого алгоритма, составим рекуррентное соотношение. Пускай T(n) - время сортировки массива длины n, тогда для сортировки слиянием справедливо T(n)=2T(n/2)+O(n) (O(n) - это время, необходимое на то, чтобы слить два массива). Распишем это соотношение:
T(n) = 2T(n/2) + O(n) = 4T(n/4) + 2O(n/2) + O(n) = 4T(n/4) + 2O(n) = … = 2kT(1) + kO(n)
Осталось оценить k. Мы знаем, что 2k = n, а значит k = log2n. Уравнение примет вид T(n) = nT(1) + log2nO(n). Так как T(1) - константа, то T(n) = O(n) + log2nO(n) = O(nlog2n). То есть, оценка времени работы сортировки слиянием меньше, чем у первых трех алгоритмов.
Лекция 13 Алгоритмы обработки строк (2 часа)
План
13.1 Строковые типы
13.2 Алгоритмы обработки строк
Строковые типы
При решении задач на ЭВМ часто возникает необходимость в использовании последовательностей символов. Такую последовательность можно описать как массив символов, однако в Паскале для таких целей имеется специальный тип - string[n] - строка из n символов, где n <= 255. Способы описания переменных - строк - аналогичны описанию массивов.
1. Строковый тип определяется в разделе описания типов, переменные этого типа - в разделе описания переменных:
type word: string[20];
vara,b,c: word;
2. Можно совместить описание строкового типа и соответствующих переменных в разделе описания переменных:
vara,b,c: string[20];
d:string[30];
3. Можно определить строковую переменную и ее начальное значение как констант-строку: const l:string[l 1]='информатика';
Символы, составляющие строку, занумерованы слева направо; к ним можно обращаться с помощью индексов, как к элементам одномерного массива. Для переменных одного строкового типа определен лексикографический порядок, являющийся следствием упорядоченности символьного типа:
'fife' < 'tree' (так как 'f' < 't'); '4' > '237' (так как '4' > '2').
Кроме логических операций <, >, =, для величин строкового типа определена некоммутативная операция соединения, обозначаемая знаком плюс:
а:='кол'+'о'+'кол'; (в результате а='колокол').
Для строковых величин определены следующие четыре стандартные функции.
1. Функция соединения - concat(sl,s2,...,sk). Значение функции - результат соединения строк sl,s2,...sk, если он содержит не более 255 символов.
2. Функция выделения - copy(s,i,k). Из строки s выделяется k символов, начиная с i-того символа:
а:=сору('крокодил',4,3); (в результате а='код*).
3. Функция определения длины строки - length(s). Вычисляется количество символов, составляющих текущее значение строки s:
b:=length('каникулы'); (b=8).
4. Функция определения позиции - pos(s,t). Вычисляется номер позиции, начиная с которого строка s входит первый раз в строку t; результат равен 0, если строка s не входит в t: с:=роs('ом','компьютер'); (с=2).
В Паскале определены также четыре стандартные процедуры для обработки строковых величин:
1. Процедура удаления delete(s,i,k). Из строки s удаляется k символов, начиная с i-того символа.
s:='таракан'; delete(s,5,2); (в результате S='таран').
2. Процедура вставки - insert(s,t,i). Строка s вставляется в строку t, начиная с позиции i:
t:='таран'; insert ('ka',t,5); (t='таракан').
3. Процедура преобразования числа в строку символов - str(k,s). Строка s получается «навешиванием» апострофов на число k: str(564,s); (s='564').
4. Процедура преобразования строки из цифр в число - val(s,k,i). Число i=0, если в строке s нет символов, отличных от цифр, в противном случае i=позиции первого символа, отличного от цифры: val('780',k,i); (k=780; i=0).
Алгоритмы обработки строк
Рассмотрим несколько программ, в которых используются строковые величины.
1. Составить программу, определяющую количество гласных в русском тексте, содержащем не более 100 с имволов.
Здесь удобно определить констант-строку, состоящую из всех 18 строчных и заглавных русских букв, и в цикле проверить, будет ли очередной символ заданного текста элементом констант-строки.
Программа 11
programvowel;
const с:зtring[18]='аеиоуыэюяАЕИОУЫЭЮЯ';
var a:string[100]; k,n:integer;
begin
writeln('введитетекст'); readln(a);n:=0;
for k:=l to length(a) do
ifpos(a[k],c)>0 then n:=n+l;
writeln('кол. гласных=',n) end.
2. Заменить в арифметическом выражении функцию sqr на ехр. Замена выражения sqr на ехр достигается последовательным применением процедур delete и insert:
Программа 12
programstroka;
vara,b:string[40]; k:integer;
begin
writeln('введите строку <= 40 символов');
readin(a);b:=a;
repeat k:=pos('sqr',b);
if k>0 then
begin
delete(b,k,3);insert('ехр',b,k);
end
until k=0;
writein('стараястрока=',a); writein('новаястрока"',b);
end.
3. Ввести и упорядочить по алфавиту 10 латинских слов. В программе определим массив из 10 элементов-строк и упорядочим его элементы методом пузырька.
Программа 13
program order;
const s=10;
type word=string(20];
var i, j, k: 1.. s;
b:word; p:boolean; list:array[l..s] of word;
begin
clrscr;writeln<'введитесписокслов');
for i:=l to s do readln(list[i]);
repeat p:=true;
for i:=s downto 2 do
if list[i]<list[i-l] then
begin
b:list[i);list[i]:=list[i-l]; list[i-l]:=b;p:=false end
untilp=true;
writein('упорядоченный список слов:');
for i:=l to s do writeln(list[i])
end.
Лекция 14. Рост функций. Формула Стирлинга(2 часа)
План
14.1 Порядок (скорости) роста
14.2 Формула Стирлинга
14.1 Порядок (скорости) роста
Те, кто часто решает алгоритмические задачи, знают, что решить их можно по-разному и, что процессы могут значительно различаться по количеству вычислительных ресурсов, которые они потребляют. Удобным способом описания этих различий является понятие порядка(скорости) роста, которое дает общую оценку ресурсов, необходимых процессу при увеличении его входных данных.
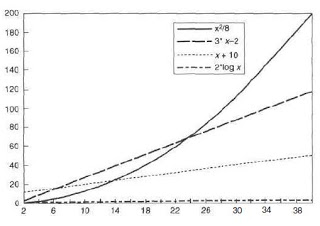
Пусть n — параметр, измеряющий размер задачи, и пусть R(n) — количество ресурсов, необходимых процессу для решения задачи размера n. R(n) может измерять количество используемых целочисленных регистров памяти, количество исполняемых элементарных
машинных операций, и так далее. В компьютерах, которые выполняют определенное число операций за данный отрезок времени, требуемое время будет пропорционально необходимому числу элементарных машинных операций.
· Омега большое
Класс функций, растущих по крайней мере так же быстро, как f, мы обозначаем через Ω(f) (читается омега большое]. Функция g при- надлежит этому классу, если при всех значениях аргумента n, больших некоторого порога по, значение g(n) > сf(n) для некоторого положи- тельного числа с. Можно считать, что класс Ω(f) задается указанием свой нижней границы: все функции из него растут по крайней мере так же быстро, как f. Мы занимаемся эффективностью алгоритмов, поэтому класс Ω(f) не будет представлять для нас большого интереса: например, в Ω(n2) входят все функции, растущие быстрее, чем n2, скажем n3 и 2n.
· О большое
На другом конце спектра находится класс O(f) (читается о большое). Этот класс состоит из функций, растущих не быстрее f. Функция f образует верхнюю границу для класса O(f). С формальной точки зрения функция g принадлежит классу О(f), если g(n)≤с/(n) для всех n, больших некоторого порога по, и для некоторой положительной константы с. т.е. g? O(f), если
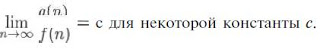
По правилу Лопиталя, в таком случае можно заменить предел самих функций пределом их производных.
· Тета большое
Через θ(f) (читается тета большое) мы обозначаем класс функций, растущих с той же скоростью, что и f. С формальной точки зрения этот класс представляет собой пересечение двух предыдущих классов, θ(f)=Ω(f) П O(f) Мы говорим, что R(n) имеет порядок роста θ (f(n)), что записывается R(n) = θ (f(n)), если существуют положительные постоянные k1 и k2, независимые от n, такие, что
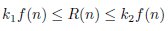
для всякого достаточно большого n. (Другими словами, значение R(n) заключено между k1f(n) и k2f(n).)
Пример
Для линейно рекурсивного процесса вычисления факториала, число шагов растет пропорционально входному значению n. Таким образом, число шагов, необходимых этому процессу, растет как θ (n). Мы видели также, что требуемый объем памяти растет как θ (n). Для итеративного факториала число шагов по-прежнему θ (n), но объем памяти θ (1) — то есть константа. Древовиднорекурсивное вычисление чисел Фибоначчи требует θ (Ψn) шагов и θ (n) памяти, где Ψ — золотое сечение.
Порядки роста дают всего лишь грубое описание поведения процесса. Например, процесс, которому требуется n2 шагов, процесс, которому требуется 1000n2 шагов и процесс, которому требуется 3n2 + 10n + 17 шагов — все имеют порядок роста θ (n2). С другой стороны, порядок роста показывает, какого изменения можно ожидать в поведении процесса, когда мы меняем размер задачи. Для процесса с порядком роста θ (n) (линейного) удвоение размера задачи примерно удвоит количество используемых ресурсов. Для экспоненциального процесса каждое увеличение размера задачи на единицу будет умножать количество ресурсов на постоянный коэффициент.
14.2 Формула Стирлинга
Разложение функции ln (1 + x) в степенной ряд дает возможность легко получить асимптотическую формулу для факториала n! при n 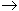
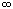 . Эта формула называется формулой Стирлинга; она имеет вид
. Эта формула называется формулой Стирлинга; она имеет вид
т. е. отношение n! к выражению, стоящему в правой части этой формулы, стремится к 1 при n 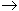
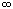 .
.
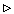 Действительно, если | x | < 1, то
Действительно, если | x | < 1, то
ln 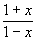 = ln (1 + x) - ln (1 - x) =
= ln (1 + x) - ln (1 - x) = 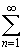 (-1) n +1 xn/n -
(-1) n +1 xn/n - 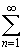 (xn/n) = 2 x
(xn/n) = 2 x 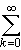 x 2 n /(2 k + 1).
x 2 n /(2 k + 1).
Положив x = 1/(2 n + 1), n = 1, 2,... получим
ln (1 + 1/ n) = 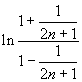 =
=
= 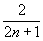
 1 +
1 + 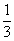
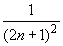 +
+ 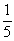
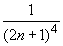 +...
+...  >
> 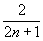 =
= 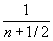 ,
,
откуда
(n + 1/2)ln (n + 1/2) > 1.
Пропотенцировав и заметив, что функция ln x возрастает, а 1 = ln e, получим
| (n + 1/2)(n +1/2) > e.
| (32.77)
|
Положим
xn =  . .
| (32.78)
|
Поскольку, согласно неравенству (32.77),
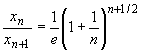 >1,
>1,
то последовательность { xn } убывает. Кроме того, она ограничена снизу: xn > 0. Следовательно, она имеет конечный предел. Обозначим его a:
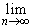 xn = a. xn = a.
| (32.79)
|
Покажем, что a 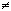 0. Так как
0. Так как
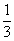
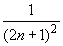 +
+ 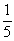
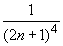 +... <
+... < 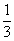

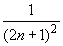 +
+ 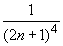 +...
+...  =
= 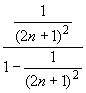 =
= 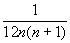 ,
,
то
(n + 1/2)ln (n + 1/2) < 1 + 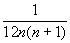
и, следовательно,
(1 + 1/n) n +1/2 < e 1+1/(12 n (n +1)).
Поэтому
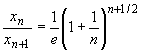 < e 1+1/(12 n (n +1)) =
< e 1+1/(12 n (n +1)) = 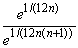 .
.
т. е.
| xne -1/(12 n) < xn +1 e -1/(12 n (n +1)).
| (32.80)
|
Последовательность yn = xne -1/(12 n), n = 1, 2,..., будучи произведением двух последовательностей { xn } и { e -1/(12 n)}, имеющих предел, также имеет предел, причем
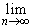 yn =
yn = 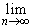 xn
xn 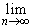 e -1/(12 n)
e -1/(12 n)  a.
a.
Неравенство (32.80) означает, что последовательность { yn } возрастает, поэтому yn, а так как yn > 0, то доказано, что a > 0.
Из равенства (32.79) следует, что
xn = a (1 +  n), n),
| (32.81)
|
где 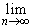
 n = 0. Подставив (32.81) в (32.78), получим
n = 0. Подставив (32.81) в (32.78), получим
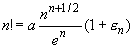
| (32.82)
|
Для того чтобы найти значение числа a, вспомним, что по формуле Валлиса (см. (26.9) в п. 26.2)
 . .
| (32.83)
|
Из формулы (32.82) следует, что
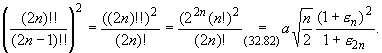
Подставив это выражение в формулу Валлиса (32.83), получим
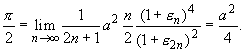
| (32.84)
|
откуда a = 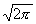 . Следовательно,
. Следовательно,
n! = 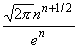 (1 +
(1 +  n),
n), 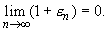
т. е. формула Стирлинга (32.76) доказана. 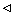
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ И УКАЗАНИЯ по выполнению ЛАБОРАТОРНЫХ РАБОТ
дисциплины
«Алгоритмы, структуры данных и программирование»
|
№
|
Наименование лабораторных занятий
| Коли чество часов
|
| 1
| Лабораторная работа №1. Основные принципы алгоритмизации и программирования. Базовые алгоритмы и программы.
| 1
|
| 2
| Лабораторная работа № 2.Программирование разветвлений Условный оператор.
| 1
|
| 3
| Лабораторная работа №3. Программирование циклов. Операторы цикла.
| 1
|
| 4
| Лабораторная работа №4. Обработка одномерных массивов.
| 2
|
| 5
| Лабораторная работа №5. Обработка двумерных массивов
| 2
|
| 6
| Лабораторная работа №6. Структурированный тип данных: строковые данные.
| 2
|
| 7
| Лабораторная работа №7. Записи и множества.
| 1
|
| 8
| Лабораторная работа №8. Подпрограммы. Процедуры и функции. Рекурсия.
| 2
|
| 9
| Лабораторная работа №9. Файлы. Работа с файлами.
| 1
|
| 10
| Лабораторная работа №10. Использование стандартных модулей. Графический редактор Graph.
| 2
|
|
| Всего:
| 15
|
ЛАБОРАТОРНАЯ РАБОТА 1 (1 час)
.Тема: Основные принципы алгоритмизации и программирования.




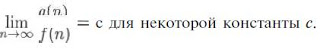
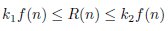
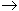
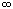 . Эта формула называется формулой Стирлинга; она имеет вид
. Эта формула называется формулой Стирлинга; она имеет вид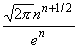 , n
, n 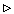 Действительно, если | x | < 1, то
Действительно, если | x | < 1, то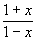 = ln (1 + x) - ln (1 - x) =
= ln (1 + x) - ln (1 - x) = 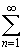 (-1) n +1 xn/n -
(-1) n +1 xn/n - 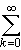 x 2 n /(2 k + 1).
x 2 n /(2 k + 1).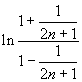 =
=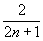
 1 +
1 + 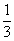
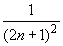 +
+ 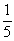
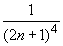 +...
+...  >
> 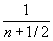 ,
, .
.
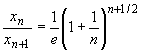 >1,
>1,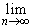 xn = a.
xn = a.
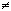 0. Так как
0. Так как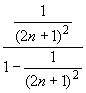 =
= 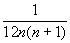 ,
,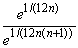 .
. a.
a. n),
n),
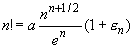
 .
.
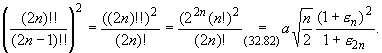
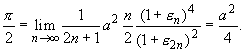
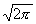 . Следовательно,
. Следовательно,