Пусть х1, х2, х3,…, х i - ряд измерений одной и той же величины. Требуется найти СКП одного измерения. Составляем отклонения Δ данных измерений от их истинного значения а:
Δ1 = а - х 1
Δ2 = а - х 2
Δ3 = а - х 3
……………
Δ i = а - х i (1)
Все измерения равноточные, но истинное значение измеряемой величины не известно. Однако вероятнейшее значение измеряемой величины является арифметическим средним  . Составим отклонения
. Составим отклонения  данных непосредственного измерения от
данных непосредственного измерения от  :
:
 1 =
1 =  - х1
- х1
 2 =
2 =  - х2
- х2
 3 =
3 =  - х3
- х3
…………
 i =
i =  - х i (2)
- х i (2)
К правой части равенства (1) отнимем и прибавим  , от чего равенства не нарушатся:
, от чего равенства не нарушатся:
Δ1 = а -  +
+  - х 1
- х 1
Δ2 = а -  +
+  - х 2
- х 2
Δ3 = а -  +
+  - х 3
- х 3
……………………
Δ i = а -  +
+  - х i
- х i
или
Δ1 = а -  +
+ 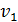
Δ2 = а -  +
+ 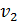
Δ3 = а -  +
+ 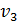
……………
Δ i = а -  +
+ 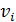
Возведем эти равенства в квадрат:
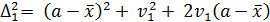


……………….……………………..

Сложив левую и правую части равенства, получим уравнение:
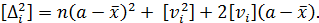
Выше доказано, что [ 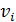 ] = 0, тогда уравнение можно переписать в виде
] = 0, тогда уравнение можно переписать в виде
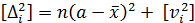 .
.
Согласно определению СКП (вспомним формулу Гаусса)
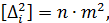
где т – искомая СКП;
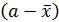 есть отклонение среднего арифметического от истинного значения измеряемой величины, т. е. другими словами, погрешность арифметической середины:
есть отклонение среднего арифметического от истинного значения измеряемой величины, т. е. другими словами, погрешность арифметической середины:

следовательно

Далее, подставляя в уравнение значения СКП и арифметической середины, получим:
 +
+ 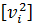 ,
,
п · т 2 - т 2 = 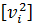 т 2 · (п – 1) =
т 2 · (п – 1) = 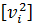 .
.
Из последнего выражения определим СКП

Таким образом, не зная истинной величины, мы через вероятнейшие поправки смогли определить СКП. Это формула Бесселя удовлетворяет строгому смыслу формулы Гаусса. Сравнивая эти формулы, мы видим, что в формуле Бесселя в знаменателе (п - 1), т. е. число избыточных наблюдений.
Сама СКП, вычисленная по формуле Бесселя, имеет погрешность. Существует приближенная формула, по которой можно вычислить погрешность:
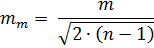
СКП арифметической середины, вычисленная через вероятнейшие поправки, определяется по формуле:
 .
.
Вычислим и проконтролируем величину 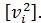 Выражение
Выражение  i =
i =  - х i
- х i
умножим на 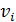 и получим:
и получим:
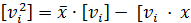 i
i 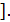
Так как 
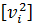 = - [
= - [ 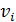 · xi ]. Вычисления по этой формуле объемные, поэтому удобнее xi процентрировать на некоторую величину х0. Принципиально не имеет значения, что будет принято за х0 данного ряда измерений.
· xi ]. Вычисления по этой формуле объемные, поэтому удобнее xi процентрировать на некоторую величину х0. Принципиально не имеет значения, что будет принято за х0 данного ряда измерений.
ε i = х i – х0,
где ε i – центрированное значение;
х0 – принято наименьшее значение из ряда измерений,тогда
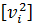 = - [
= - [ 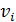 · ε i ].
· ε i ].
Если  получено с округлением, то контроль
получено с округлением, то контроль 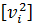 не будет выполняться. В этом случае для точного контроля может быть использована формула:
не будет выполняться. В этом случае для точного контроля может быть использована формула: 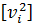 = - [
= - [ 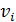 · ε i ] + (
· ε i ] + ( - х0) · [
- х0) · [ 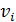 ] или
] или
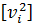 = - [
= - [ 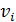 · ε i ] + [ε i ] · ω + п · ω2
· ε i ] + [ε i ] · ω + п · ω2
При математической обработке, если не сходится контроль [ 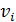 ] = 0 или [
] = 0 или [ 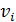 ] = п · ω, дальнейшие вычисления следует прекратить и искать ошибку. То же, если не сходиться второй контроль.
] = п · ω, дальнейшие вычисления следует прекратить и искать ошибку. То же, если не сходиться второй контроль.
Пример. При определении координат дополнительного пункта методом обратной засечки (задача Потенота) измерено направление 10-7 четырьмя приемами теодолитом 3Т-2КП. Результаты измерения представлены в таблице:
| №п/п
| Результаты х i
| εi
| v i
| v i2
| v i · εi
|
| 1
| 72°45'32''
| 3
| +1
| 1
| +3
|
| 2
| 72°45'34''
| 5
| -1
| 1
| -5
|
| 3
| 72°45'29''
| 0
| +4
| 16
| 0
|
| 4
| 72°45'35''
| 6
| -2
| 4
| -12
|
[14] [+2] [22] [-14]
Выполнить математическую обработку результатов измерений.
х0 = 72°45'29'', определяем εi = х i – х0.
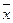 = х0 +
= х0 + 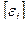 = 72°45'29'' +
= 72°45'29'' + 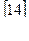 = 72°45'32,5''. Округляем
= 72°45'32,5''. Округляем 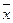 до 72°45'33'', тогда погрешность округления ω = + 0,5.
до 72°45'33'', тогда погрешность округления ω = + 0,5.
Вероятнейшие поправки определяются по формуле vi = 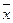 - х i
- х i
Контроль: 1.  , [+2] = 4 · (+0,5);
, [+2] = 4 · (+0,5);
2. [ vi2 ] = - [ v i · εi] + (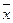 - х0)·[ v i] = 14 + (72°45'33'' - 72°45'29'') · 2 = 22.
- х0)·[ v i] = 14 + (72°45'33'' - 72°45'29'') · 2 = 22.
Оба контроля сходятся.
Определим СКП по формуле Бесселя 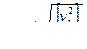 =
=  = ± 2",7.
= ± 2",7.
СКП арифметического среднего  =
=  = ± 1",4.
= ± 1",4.



 . Составим отклонения
. Составим отклонения  данных непосредственного измерения от
данных непосредственного измерения от 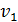
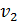
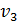
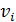
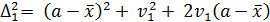



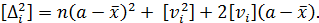
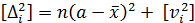 .
.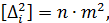
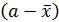 есть отклонение среднего арифметического от истинного значения измеряемой величины, т. е. другими словами, погрешность арифметической середины:
есть отклонение среднего арифметического от истинного значения измеряемой величины, т. е. другими словами, погрешность арифметической середины:

 +
+ 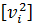 ,
,
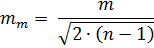
 .
.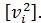 Выражение
Выражение 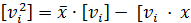 i
i 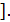

 получено с округлением, то контроль
получено с округлением, то контроль 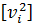 = - [
= - [  - х0) · [
- х0) · [ 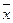 = х0 +
= х0 + 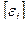 = 72°45'29'' +
= 72°45'29'' + 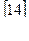 = 72°45'32,5''. Округляем
= 72°45'32,5''. Округляем  , [+2] = 4 · (+0,5);
, [+2] = 4 · (+0,5);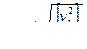 =
=  = ± 2",7.
= ± 2",7. =
=  = ± 1",4.
= ± 1",4.

